В функции эффективности среднеквадратичной погрешности по умолчанию (см., Обучают и Применяют Многоуровневые Мелкие Нейронные сети), каждая квадратичная невязка вносит ту же сумму в функцию эффективности можно следующим образом:
Однако тулбокс позволяет вам взвешивать каждую квадратичную невязку индивидуально можно следующим образом:
Ошибка при взвешивании объекта должна иметь те же размерности как целевые данные. Таким образом ошибки могут быть взвешены согласно временному шагу, демонстрационному номеру, номеру сигнала или номеру элемента. Следующее является примером взвешивания ошибок в конце последовательности времени в большей степени, чем ошибки в начале последовательности времени. Ошибка при взвешивании объекта передается в качестве последнего аргумента в вызове train.
y = laser_dataset; y = y(1:600); ind = 1:600; ew = 0.99.^(600-ind); figure plot(ew)

ew = con2seq(ew);
ftdnn_net = timedelaynet([1:8],10);
ftdnn_net.trainParam.epochs = 1000;
ftdnn_net.divideFcn = '';
[p,Pi,Ai,t,ew1] = preparets(ftdnn_net,y,y,{},ew);
[ftdnn_net1,tr] = train(ftdnn_net,p,t,Pi,Ai,ew1);Фигура иллюстрирует ошибку при взвешивании для этого примера. В обучающих данных существует 600 временных шагов, и ошибки взвешиваются экспоненциально с последней квадратичной невязкой, имеющей вес 1 и квадратичной невязкой на первом временном шаге, имеющем взвешивание 0,0024.
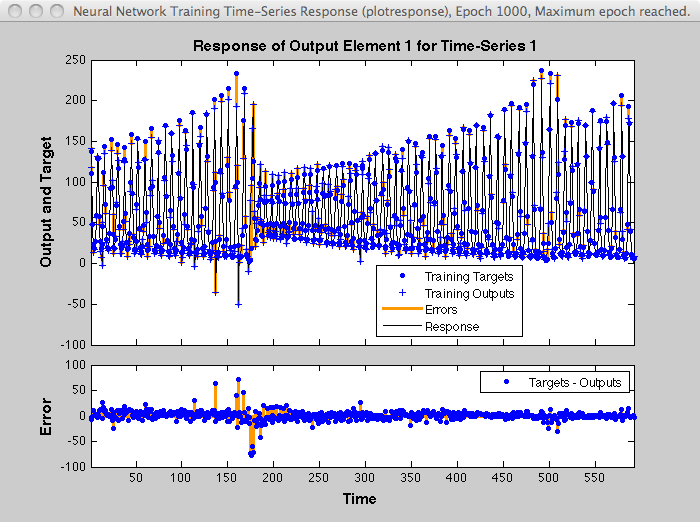
Ответ обучившего сеть показывают в следующем рисунке. Если вы сравниваете этот ответ на ответ сети, которая была обучена без экспоненциального взвешивания на квадратичных невязках, как показано в Серийных Нейронных сетях Задержки Времени проектирования, вы видите, что ошибки поздно в последовательности меньше, чем ошибки ранее в последовательности. Ошибки, которые произошли позже, меньше, потому что они способствовали больше взвешенному индексу эффективности, чем более ранние ошибки.