Нули, полюса и усиление lowpass к полосовому преобразованию частоты
[Z2,P2,K2,AllpassNum,AllpassDen]
= zpklp2bp(Z,P,K,Wo,Wt)
[Z2,P2,K2,AllpassNum,AllpassDen]
= zpklp2bp(Z,P,K,Wo,Wt) возвращает нули, Z2, полюса, P2, и фактор усиления, K2, целевого фильтра, преобразованного от действительного lowpass, моделируют путем применения действительного lowpass второго порядка к действительному полосовому отображению частоты.
Это также возвращает числитель, AllpassNum, и знаменатель AllpassDen, из allpass, сопоставляющего фильтр. Прототип фильтр lowpass дан с нулями, Z, полюса, P, и фактор усиления, K.
Это преобразование эффективно помещает одну функцию исходного фильтра, расположенного на частоте - Во, на необходимом целевом местоположении частоты, Wt1 и второй функции, первоначально в +Во, в новом местоположении, Wt2. Это принято, что Wt2 больше Wt1. Это преобразование реализует "Мобильность DC", что означает, что функция Найквиста остается в Найквисте, но функция DC перемещается в местоположение, зависящее от выбора Wt.
Относительные положения других функций исходного фильтра не изменяются в целевом фильтре. Это означает, что возможно выбрать две функции исходного фильтра, F1 и F2, с F1, предшествующим F2. F1 функции будет все еще предшествовать F2 после преобразования. Однако расстояние между F1 и F2 не будет тем же самым до и после преобразования.
Выбор функции, удовлетворяющей lowpass к полосовому преобразованию, не ограничивается только частотой среза исходного фильтра lowpass. В целом возможно выбрать любую функцию; e.g., ребро полосы задерживания, DC, глубокий минимум в полосе задерживания или другие единицы.
Действительный lowpass к полосовому преобразованию может также использоваться для преобразования других типов фильтров; e.g., действительные фильтры метки или резонаторы могут быть легко удвоены и расположены в две отличных, желаемых частоты.
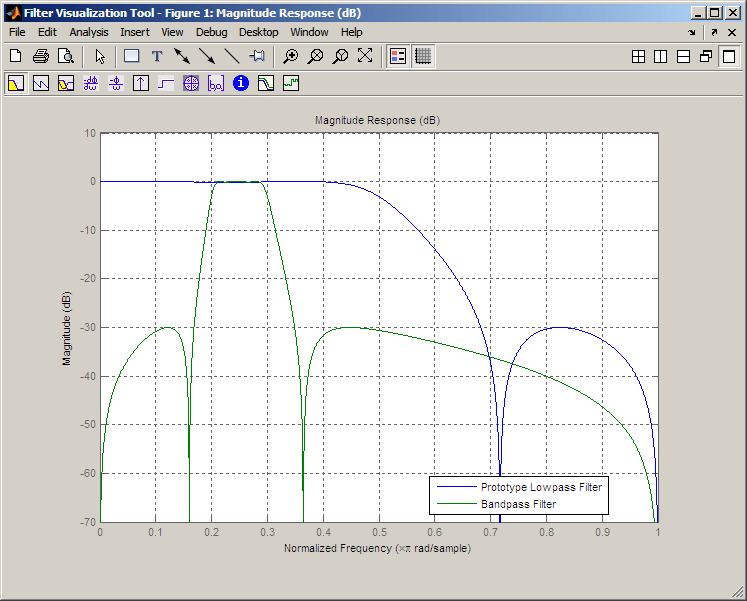
Спроектируйте прототип действительный БИХ-полуленточный фильтр с помощью стандартного эллиптического подхода:
[B,A] = ellip(3,0.1,30,0.409); Z = roots(B); P = roots(A); K = B(1); [Z2,P2,K2] = zpklp2bp(Z,P,K, 0.5, [0.2 0.3]); hfvt = fvtool(B,A,K2*poly(Z2),poly(P2)); legend(hfvt,'Prototype Lowpass Filter', 'Bandpass Filter'); axis([0 1 -70 10]);
| Переменная | Описание |
|---|---|
Z | Нули прототипа фильтр lowpass |
P | Полюса прототипа фильтр lowpass |
K | Фактор усиления прототипа фильтр lowpass |
Wo | Значение частоты, которое будет преобразовано от прототипного фильтра |
Wt | Желаемое местоположение частоты в преобразованном целевом фильтре |
Z2 | Нули целевого фильтра |
P2 | Полюса целевого фильтра |
K2 | Фактор усиления целевого фильтра |
AllpassNum | Числитель фильтра отображения |
AllpassDen | Знаменатель фильтра отображения |
Частоты должны быть нормированы, чтобы быть между 0 и 1 с 1 соответствием половине частоты дискретизации.
Constantinides, A.G., “Спектральные преобразования для цифровых фильтров”, Продолжения IEE, издание 117, № 8, стр 1585-1590, август 1970.
Nowrouzian, B. и А.Г. Констэнтинайдс, “Параметры передаточной функции ссылки прототипа в преобразованиях частоты дискретного времени”, Продолжения 33-й Среднезападный Симпозиум по Схемам и Системам, Калгари, Канада, изданию 2, стр 1078-1082, август 1990.
Nowrouzian, B. и Л.Т. Брутон, “Решения Закрытой формы в течение дискретного времени эллиптические передаточные функции”, Продолжения 35-го Среднезападного Симпозиума по Схемам и Системам, изданию 2, стр 784-787, 1992.
Constantinides, A.G., “Проект полосовых цифровых фильтров”, IEEE® Proceedings, издание 1, стр 1129-1231, июнь 1969.