Документация

Введение

Программное обеспечение Financial Instruments Toolbox™ поддерживает вычисления, связанные с типовыми ипотечными пулами с фиксированной процентной ставкой и займами со вздутыми выплатами. Типовые ипотечные пулы с фиксированной процентной ставкой и займы со вздутыми выплатами имеют сертификаты передачи (PC), которые обычно встраивали колл-опционы в форме предварительной оплаты. Предварительная оплата является избыточной оплатой, применился к принципалу PC. Эти ускоренные платежи уменьшают эффективную жизнь PC.

Тулбокс идет со стандартной Ассоциацией Рынка облигаций (PSA) модель предварительной оплаты и может сгенерировать множители стандартных скоростей предварительной оплаты. Общедоступная Ассоциация рынка ценных бумаг обеспечивает набор универсальных методов для вычисления характеристик ценных бумаг, обеспеченных закладной, когда существует принятая функция предварительной оплаты.

В качестве альтернативы кроме стандартной реализации PSA в этом тулбоксе, можно предоставить собственные спроектированные векторы предварительной оплаты. В настоящее время, однако, пользовательская функциональность предварительной оплаты, которая включает специфичную для пула информацию и прогнозы процентной ставки, не доступна в этом тулбоксе. Если вы планируете использовать пользовательские векторы предварительной оплаты в своих вычислениях, вы, по-видимому, уже владеете таким набором в MATLAB^®.

Входные параметры функций

Из-за типовой, универсальной природы функций передачи тулбокса можно подстроить их, чтобы соответствовать конкретной ипотеке. Большинство функций требует, по крайней мере, этого набора входных параметров:

Типичные дополнительные входные параметры включают стандартную скорость предварительной оплаты (или настроенный вектор), сетевая купонная ставка (если отличающийся от грубой купонной ставки), и платежная задержка номера дней.

Все вычисления основаны на ожидаемых платежных днях и фактическом потоке наличности инвестору. Например, когда GrossRate и CouponRate отличайтесь как входные параметры к mbsdurp, функция возвращает модифицированную длительность на основе CouponRate. (Существенное исключение mbspassthrough, который возвращает количества интереса на основе GrossRate.)

Генерация векторов предварительной оплаты

Можно сгенерировать PSA несколько векторов предварительной оплаты быстро. Чтобы сгенерировать векторы предварительной оплаты из 100 и 200 PSA, ввести

PSASpeed = [100, 200];
[CPR, SMM] = psaspeed2rate(PSASpeed);

Эта функция вычисляет два значения предварительной оплаты: условный уровень предварительной оплаты (CPR) и уровень одного ежемесячного выхода из строя (SMM). CPR является процентом выдающегося принципала, предварительно оплаченного за один год. SMM является процентом выдающегося принципала, предварительно оплаченного за один месяц. Другими словами, CPR является ежегодной версией SMM.

Начиная с целого 360 2 массив является слишком длинным, чтобы показать в этом документе, наблюдать SMM (100 и 200 PSA) графики, расположенные с интервалами на расстоянии в один месяц, вместо этого.

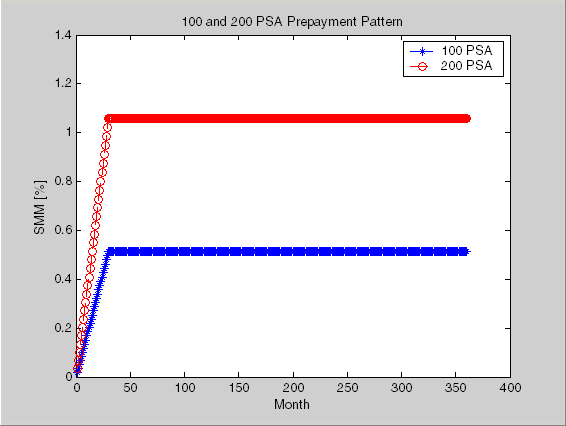
Предположения предварительной оплаты формируют базис, на котором базируются намного более всесторонние вычисления MBS. Как рисунок, наблюдайте следующий пример, который показывает использование функции mbscfamounts сгенерировать потоки наличности и синхронизации на основе набора стандартных предварительных оплат.

Рассмотрите три ипотечных пула, которые были проданы на дате выпуска (который запускается неамортизированный). Первые два пула "воздушный шар" за 60 месяцев и третье регулярно амортизируются в конец. Скорости предварительной оплаты приняты, чтобы быть 100, 200, и 200 PSA, соответственно.

Settle     = [datenum('1-Feb-2000');
              datenum('1-Feb-2000');
              datenum('1-Feb-2000')];
                            
Maturity   = [datenum('1-Feb-2030')];
          
IssueDate  = datenum('1-Feb-2000');
GrossRate  = 0.08125;
CouponRate = 0.075;
Delay = 14; 

PSASpeed = [100, 200];
[CPR, SMM] = psaspeed2rate(PSASpeed);

PrepayMatrix = ones(360,3);
PrepayMatrix(1:60,1:2) = SMM(1:60,1:2);
PrepayMatrix(:,3) = SMM(:,2);

[CFlowAmounts, CFlowDates, TFactors, Factors] = ... 
mbscfamounts(Settle, Maturity, IssueDate, GrossRate, ... 
CouponRate, Delay, [], PrepayMatrix);

Четвертый выходной аргумент, Factors, указывает на часть баланса, все еще выдающегося в начале каждого месяца. Снимок состояния этого аргумента в редакторе переменных MATLAB иллюстрирует 60-месячную жизнь первых двух из ипотек с крупными разовыми платежами в погашение долга и продолжением третьей ипотеки до конца (360 месяцев).

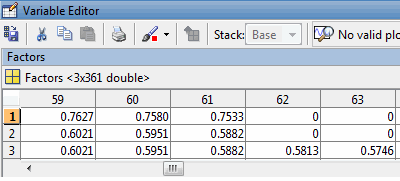
Можно с готовностью видеть тот mbscfamounts базовый блок большей части фиксированной процентной ставки и потоков наличности пула воздушного шара.

Заложите предварительные оплаты

Предварительная оплата выгодна для владельца передачи, когда ипотечный пул был куплен со скидкой. Следующий пример сравнивает ипотечные выражения (составленный ежемесячно) по сравнению с покупкой чистая цена с постоянной скоростью предварительной оплаты. Пример иллюстрирует, что, когда вы купили пул со скидкой, предварительная оплата генерирует более высокое выражение с уменьшением покупной цены.

Price = [85; 90; 95];
Settle = datenum('15-Apr-2002');
Maturity = datenum('1 Jan 2030');
IssueDate = datenum('1-Jan-2000');
GrossRate = 0.08125;
CouponRate = 0.075;
Delay = 14;
Speed = 100;

Вычислите ипотеку и доходности по облигациям.

[MYield, BEMBSYield] = mbsyield(Price, Settle, Maturity, ... 
IssueDate, GrossRate, CouponRate, Delay, Speed)

MYield =

    0.1018
    0.0918
    0.0828

BEMBSYield =

    0.1040
    0.0936
    0.0842

Если для этого того же пула ипотек, не было никакой предварительной оплаты (Speed = 0), выражения уменьшились бы к

MYield =

    0.0926
    0.0861
    0.0802

BEMBSYield =

    0.0944
    0.0877
    0.0815

Аналогично, если уровень удвоенной предварительной оплаты (Speed = 200), выражения увеличились бы до

MYield =

    0.1124
    0.0984
    0.0858

BEMBSYield =

    0.1151
    0.1004
    0.0873

Для того же вектора предварительной оплаты глубже обесценьте пулы, зарабатывают более высокие выражения. Для получения дополнительной информации смотрите mbsprice и mbsyield.

Рискните измерением

Financial Instruments Toolbox обеспечивает самые основные меры по риску портфеля пула:

Рассмотрите следующий пример, который вычисляет Маколея и измененную длительность, учитывая цену ипотечного пула.

Price = [95; 100; 105];
Settle = datenum('15-Apr-2002');
Maturity = datenum('1-Jan-2030');
IssueDate = datenum('1-Jan-2000');
GrossRate = 0.08125;
CouponRate = 0.075;
Delay = 14;
Speed = 100;
 
[YearDuration, ModDuration] = mbsdurp(Price, Settle, ...
Maturity, IssueDate, GrossRate, CouponRate, Delay, Speed)

YearDuration =

    6.1341
    6.3882
    6.6339

ModDuration =

    5.8863
    6.1552
    6.4159

Используя функции Financial Instruments Toolbox, можно получить измененную длительность и выпуклость или от цены или от выражения, пока вы задаете вектор предварительной оплаты или принятую скорость предварительной оплаты. Функции измерения риска тулбокса (mbsdurp, mbsdury, mbsconvp, mbsconvy, и mbswal) придерживайтесь инструкций, перечисленных в Универсальном руководстве Методов PSA.

Оценка ипотечного пула

Для точной оценки ипотечного пула необходимо сгенерировать пути процентной ставки и использовать их с характеристиками ипотечного пула, чтобы правильно оценить пул. Широко используемая методология является настроенным опцией распространением (OAS). OAS измеряет распространение выражения, которое не непосредственно относится к характеристикам инвестиций фиксированного дохода.