Бросьте от, удваивается до фиксированной точки

Этот пример показывает вам, как симулировать непрерывное реальное, удваивает сигнал с помощью обобщенного типа данных с фиксированной точкой. Используя fxpdemo_dbl2fix модель, можно исследовать многие важные функции программного обеспечения Fixed-Point Designer™, включая

Типы данных
Масштабирование
Округление
Логгирование минимальных и максимальных значений симуляции к рабочей области
Обработка переполнения

Чтобы открыть модель, в командной строке MATLAB^®, входят

fxpdemo_dbl2fix

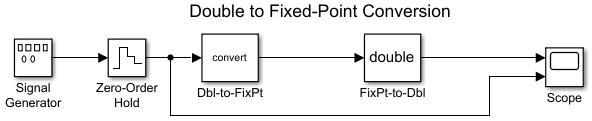
В этом примере вы конфигурируете блок Signal Generator, чтобы вывести синусоидальный сигнал с амплитудой, заданной на интервале [-5 5]. Блок Signal Generator всегда выходные параметры числа с двойной точностью.

Dbl-to-FixPt Блок Data Type Conversion преобразует числа с двойной точностью от блока Signal Generator в один из типов данных Fixed-Point Designer. Для простоты размер выходного сигнала составляет 5 битов в этом примере.

FixPt-to-Dbl Блок Data Type Conversion преобразует один из типов данных Fixed-Point Designer в тип данных Simulink^®. В этом примере это выводит числа с двойной точностью.

Симулируйте Используя единственное двоичной точкой масштабирование

При использовании единственного двоичной точкой масштабирования ваша цель состоит в том, чтобы найти оптимальную экспоненту степени двойки E, как задано в Масштабировании. Для этого режима масштабирования дробный наклон F равняется 1 и нет никакого смещения.

Настраивать модель, чтобы использовать единственное двоичной точкой масштабирование:

Сконфигурируйте блок Signal Generator, чтобы вывести синусоидальный сигнал с амплитудой, заданной на интервале [-5 5].
1. Дважды кликните блок Signal Generator, чтобы открыть диалоговое окно Block Parameters.
2. Установите параметр Wave form на sine.
3. Установите параметр Amplitude на 5.
4. Нажмите OK.
Сконфигурируйте Data Type Conversion (Dbl-to-FixPt) блок.
1. Дважды кликните блок Dbl-to-FixPt, чтобы открыть диалоговое окно Block Parameters.
2. Проверьте, что параметром Output data type является fixdt(1,5,2). Это задает 5-битный, номер фиксированной точки со знаком с масштабированием 2^-2, который помещает двоичную точку два места слева от самого правого бита. Следовательно максимальное значение 011.11 = 3.75, минимальное значение 100.00 =-4.00, и точность (1/2) ² = 0.25.
3. Проверьте, что параметр Integer rounding mode устанавливается на Floor. Это округляет результат фиксированной точки к отрицательной бесконечности.
4. Установите флажок Saturate on integer overflow, чтобы препятствовать тому, чтобы блок перенесся на переполнении.
5. Нажмите OK.
Чтобы симулировать модель, во вкладке Simulation, нажимают Run.

Scope отображает идеал и результаты симуляции фиксированной точки.

Симуляция показывает эффекты квантования вычислений с фиксированной точкой. Используя 5-битное слово с точностью (1/2) ² = 0.25 производит дискретизированный выход, который не охватывает полный спектр входного сигнала.

Чтобы породить полную линейную оболочку столбцов входного сигнала с 5 битами с помощью единственного двоичной точкой масштабирования, установите выход, масштабирующийся на 2^-1. Это помещает двоичную точку одно место слева от самого правого бита, давая максимальное значение 0 111,1 = 7.5 и минимальное значение 1 000,0 =-8.0. Однако точность уменьшается до (1/2) ¹ = 0.5. Если вы хотите породить полную линейную оболочку столбцов входного сигнала с 5 битами с помощью единственного двоичной точкой масштабирования, то единственная опция должна пожертвовать точностью. Следовательно, выходным масштабированием является 2^-1, который помещает двоичную точку одно место слева от самого правого бита. Это масштабирование дает максимальное значение 0 111,1 = 7.5, минимальное значение 1 000,0 =-8.0, и точность (1/2) ¹ = 0.5.

Чтобы видеть эффект сокращения точности к 0,5, установите параметр Output data type Dbl-to-FixPt Блок Data Type Conversion к fixdt(1,5,1) и повторно выполненный симуляция.

Симулируйте Используя [наклонное смещение] масштабирование

При использовании [Наклонное Смещение] масштабирование, ваша цель состоит в том, чтобы найти оптимальный дробный наклон F и зафиксированную экспоненту степени двойки E, как задано в Масштабировании. Нет никакого смещения для этого примера, потому что синусоида задана на интервале [-5 5].

Чтобы найти наклон, вы начинаете путем принятия фиксированной экспоненты степени двойки-2. Чтобы найти дробный наклон, разделите максимальное значение синусоиды максимальным значением масштабированного 5-битного номера. Результатом является 5.00/3.75 = 1.3333. Наклон (и точность) 1.3333 (0.25) = 0.3333. Вы задаете [Наклонное Смещение] масштабирующийся как [0.3333 0] путем ввода выражения fixdt(1,5,0.3333,0) как значение параметра Output data type.

Вы могли также задать фиксированную экспоненту степени двойки-1 и соответствующий дробный наклон 0,6667. Получившийся наклон является тем же самым, поскольку E уменьшается на 1 бит, но F увеличен на 1 бит. Программное обеспечение Fixed-Point Designer автоматически сохранило бы F как 1,3332 и E как-2 из-за условия нормализации 1 ≤ F <2.

Настраивать модель, чтобы использовать [Наклонное Смещение] масштабирование:

Сконфигурируйте блок Signal Generator, чтобы вывести синусоидальный сигнал с амплитудой, заданной на интервале [-5 5].
1. Дважды кликните блок Signal Generator, чтобы открыть диалоговое окно Block Parameters.
2. Установите параметр Wave form на sine.
3. Установите параметр Amplitude на 5.
4. Нажмите OK.
Сконфигурируйте Dbl-to-FixPt Блок Data Type Conversion.
1. Дважды кликните блок Dbl-to-FixPt, чтобы открыть диалоговое окно Block Parameters.
2. Чтобы задать [Наклонное Смещение] масштабирование [0.3333 0], установите параметр Output data type на fixdt(1,5,0.3333,0).
3. Проверьте, что параметром Integer rounding mode является Floor. Это округляет результат фиксированной точки к отрицательной бесконечности.
4. Установите флажок Saturate on integer overflow, чтобы препятствовать тому, чтобы блок перенесся на переполнении.
5. Нажмите OK.
Чтобы симулировать модель, во вкладке Simulation, нажимают Run.

Scope отображает идеал и результаты симуляции фиксированной точки.

Если вы не знаете наклон, можно достигнуть разумных результатов симуляции путем выбора масштабирования на основе формулы

$\frac{(m a x_v a l u e - m i n_v a l u e)}{2^{w s} - 1},$

где

max_value является максимальным значением, которое будет симулировано
min_value является минимальным значением, которое будет симулировано
ws является размером слова в битах
2^ws - 1 самое большое значение слова с размером ws

В данном примере формула производит наклон 0,32258.

Документация