Нелинейные Ограничения Используя ga

Нелинейные ограничения Используя `ga`

Предположим, что вы хотите минимизировать простую функцию фитнеса двух переменных x ₁ и x ₂,

$\min_{x} f (x) = 100 {(x_{1}^{2} - x_{2})}^{2} + {(1 - x_{1})}^{2}$

подвергните следующим нелинейным ограничениям неравенства и границам

$\begin{array}{l} x_{1} \cdot x_{2} + x_{1} - x_{2} + 1.5 \leq 0 & (нелинейное ограничение) \\ 10 - x_{1} \cdot x_{2} \leq 0 & (нелинейное ограничение) \\ 0 \leq x_{1} \leq 1 & (связанный) \\ 0 \leq x_{2} \leq 13 & (связанный) \end{array}$

Начните путем создания ограничительных функций и фитнеса. Во-первых, создайте файл с именем simple_fitness.m можно следующим образом:

function y = simple_fitness(x)
y = 100*(x(1)^2 - x(2))^2 + (1 - x(1))^2;

Функция генетического алгоритма, ga, принимает, что функция фитнеса возьмет один вход x, где x имеет столько же элементов сколько количество переменных в проблеме. Функция фитнеса вычисляет значение функции и возвращает то скалярное значение в его одном возвращаемом аргументе, y.

Затем создайте файл, simple_constraint.m, содержа ограничения

function [c, ceq] = simple_constraint(x)
c = [1.5 + x(1)*x(2) + x(1) - x(2);...
-x(1)*x(2) + 10];
ceq = [];

ga функция принимает, что ограничительная функция возьмет один вход x, где x имеет столько же элементов сколько количество переменных в проблеме. Ограничительная функция вычисляет значения всех ограничений неравенства и ограничений равенства и возвращает два вектора, c и ceq, соответственно.

Чтобы минимизировать функцию фитнеса, необходимо передать указатель на функцию функции фитнеса в качестве первого аргумента к ga функция, а также определение количества переменных в качестве второго аргумента. Нижние и верхние границы обеспечиваются как LB и UB соответственно. Кроме того, также необходимо передать указатель на функцию нелинейной ограничительной функции.

ObjectiveFunction = @simple_fitness;
nvars = 2;    % Number of variables
LB = [0 0];   % Lower bound
UB = [1 13];  % Upper bound
ConstraintFunction = @simple_constraint;
rng(1,'twister') % for reproducibility
[x,fval] = ga(ObjectiveFunction,nvars,...
    [],[],[],[],LB,UB,ConstraintFunction)

Optimization terminated: average change in the fitness value less than options.FunctionTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =

    0.8123   12.3137


fval =

   1.3581e+04

Для проблем без целочисленных ограничений решатель генетического алгоритма обрабатывает линейные ограничения и границы по-другому по сравнению с нелинейными ограничениями. Всем линейным ограничениям и границам удовлетворяют в течение оптимизации. Однако ga может не удовлетворить всем нелинейным ограничениям при каждой генерации. Если ga сходится к решению, нелинейным ограничениям удовлетворят в том решении.

Если существуют целочисленные ограничения, ga не осуществляет выполнимость линейных ограничений, и вместо этого добавляет любые линейные нарушения ограничений в функцию штрафа. Смотрите Целое число ga Алгоритм.

ga использует мутацию и перекрестные функции, чтобы произвести новых индивидуумов при каждой генерации. ga удовлетворяет линейным и связанным ограничениям при помощи мутации и перекрестных функций, которые только генерируют допустимые точки. Например, в предыдущем вызове ga, функция мутации mutationguassian не обязательно выполняет связанные ограничения. Таким образом, когда там связаны или линейные ограничения, значение по умолчанию ga функцией мутации является mutationadaptfeasible. Если вы обеспечиваете пользовательскую функцию мутации, эта пользовательская функция должна только сгенерировать точки, которые выполнимы относительно линейных и связанных ограничений. Все включенные перекрестные функции генерируют точки, которые удовлетворяют линейным ограничениям и границам.

Чтобы видеть прогресс оптимизации, используйте optimoptions функция, чтобы создать опции тот выбор две функции построения графика. Первой функцией построения графика является gaplotbestf, который строит лучший и средний счет населения при каждой генерации. Второй функцией построения графика является gaplotmaxconstr, который строит максимальное нарушение ограничений нелинейных ограничений при каждой генерации. Можно также визуализировать прогресс алгоритма путем отображения информации к командному окну с помощью 'Display' опция.

options = optimoptions('ga','PlotFcn',{@gaplotbestf,@gaplotmaxconstr},'Display','iter');

Повторно выполнитесь ga решатель.

[x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],...
              LB,UB,ConstraintFunction,options)

                              Best       Max        Stall
Generation  Func-count        f(x)     Constraint  Generations
    1           2520       13603.6            0      0
    2           4982       13578.2    5.718e-06      0
    3           7538       14033.9            0      0
    4          11116       13573.7    0.0009577      0
Optimization terminated: average change in the fitness value less than options.FunctionTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =

    0.8122   12.3104


fval =

   1.3574e+04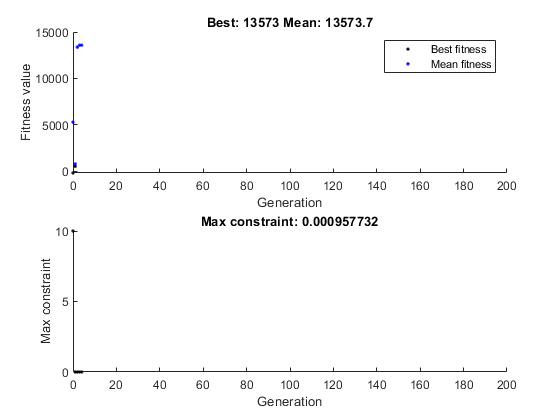

Можно обеспечить стартовую точку для минимизации к ga функция путем определения InitialPopulationMatrix опция. ga функция будет использовать первого индивидуума от InitialPopulationMatrix как стартовая точка для ограниченной минимизации.

X0 = [0.5 0.5]; % Start point (row vector)
options = optimoptions('ga',options,'InitialPopulationMatrix',X0);

Теперь повторно выполнитесь ga решатель.

[x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],...
              LB,UB,ConstraintFunction,options)

                              Best       Max        Stall
Generation  Func-count        f(x)     Constraint  Generations
    1           2520       13578.1    0.0005269      0
    2           4982       13578.2    1.815e-05      0
    3           8008       14031.3            0      0
    4          13525       14054.9            0      0
    5          17620       13573.5    0.0009986      0
Optimization terminated: average change in the fitness value less than options.FunctionTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =

    0.8122   12.3103


fval =

   1.3573e+04

Документация