В этом примере показано, как найти Множество Парето для 2D целевой функции двух переменных. Пример представляет два подхода для минимизации: использование Оптимизировать задача Live Editor и работа в командной строке.
2D целевая функция f (x), где x также двумерен,
Создайте новый live скрипт путем нажатия кнопки New Live Script в разделе File по вкладке Home.
Введите Live Editor Optimize задача. Кликните по вкладке Insert и затем, в разделе Code, выберите Task > Optimize.
Для использования во вводе проблемных данных вставьте новый раздел путем нажатия кнопки Section Break на вкладке Insert. Новые разделы появляются выше и ниже задачи.
В новом разделе выше задачи введите следующий код, чтобы задать количество переменных и нижних и верхних границ.
nvar = 2; lb = [0 -5]; ub = [5 0];
Чтобы поместить эти переменные в рабочую область, запустите раздел путем нажатия Ctrl+Enter.
Задайте проблемный тип
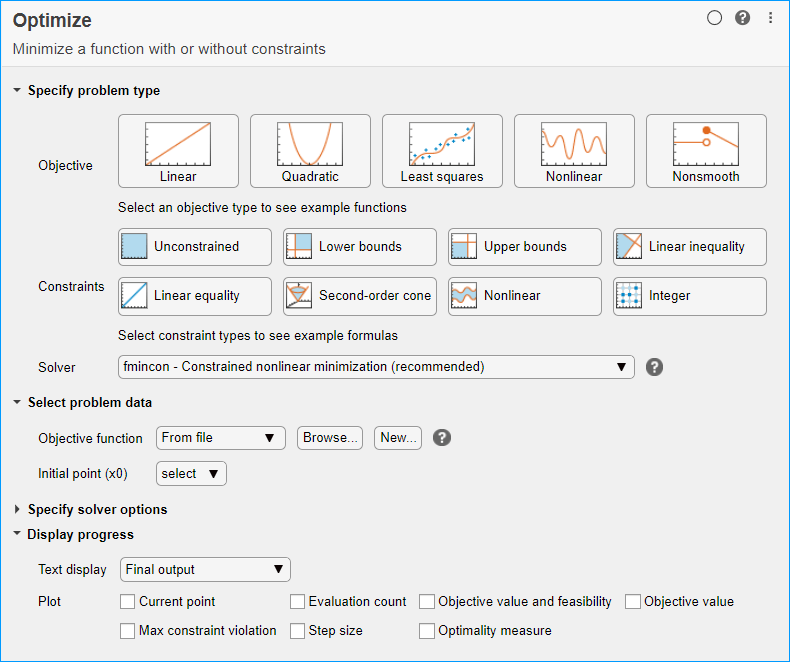
В разделе Specify problem type задачи нажмите кнопку Objective > Nonlinear.
Нажмите кнопки Constraints > Lower bounds и Upper bounds.
Выберите Solver > gamultiobj - Multiobjective optimization using genetic algorithm.
Выберите Problem Data
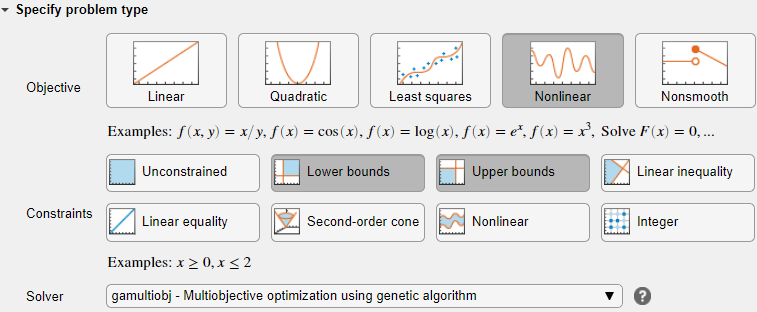
В разделе Select problem data выберите Objective function > Local function, и затем нажмите кнопку New. Функция появляется в новом разделе ниже задачи.
Отредактируйте получившееся функциональное определение, чтобы содержать следующий код.
function f = mymulti1(x) f(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - (x(1)*x(2))^2; f(1) = f(2) - 10*x(1)^2; end
В разделе Select problem data выберите функцию Local function > mymulti1.
Выберите Number of variables > nvar.
Выберите Lower bounds > From workspace > lb и Upper bounds > From workspace > ub.
Задайте опции решателя
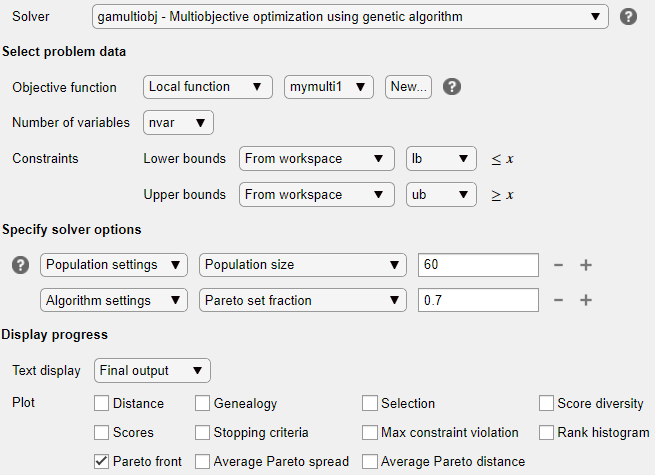
Расширьте раздел Specify solver options задачи, и затем нажмите кнопку Add. Чтобы иметь более плотную, более связанную переднюю сторону Парето, задайте более многочисленные, чем значение по умолчанию популяции путем выбора Population settings > Population size > 60.
Чтобы иметь больше населения на передней стороне Парето, чем настройки по умолчанию, нажмите кнопку +. В получившихся опциях выберите Algorithm > Pareto set fraction > 0.7.
Опции дисплея аппарата
В разделе Display progress задачи выберите функцию построения графика Pareto front.
Запустите решатель и исследуйте результаты
Чтобы запустить решатель, кликните по кнопке ⁝ опций в правом верхнем из окна задачи и выберите Run Section. График появляется в отдельном окне рисунка и в области вывода задачи.
![Set of points on a convex curve from about [-38,33] to about [-5,0]](multiobj_plot2.png)
График показывает компромисс между двумя компонентами f, который построен на пробеле целевой функции. Для получения дополнительной информации см. рисунок 9-2 фигуры, Набор Ненижних Решений.
Чтобы выполнить ту же оптимизацию в командной строке, завершите следующие шаги.
Создайте mymulti1 файл целевой функции на вашем пути MATLAB®.
function f = mymulti1(x) f(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - (x(1)*x(2))^2; f(1) = f(2) - 10*x(1)^2; end
Установите опции и границы.
options = optimoptions('gamultiobj','PopulationSize',60,... 'ParetoFraction',0.7,'PlotFcn',@gaplotpareto); lb = [0 -5]; ub = [5 0];
Запустите оптимизацию с помощью опций.
[solution,ObjectiveValue] = gamultiobj(@mymulti1,2,...
[],[],[],[],lb,ub,options);И Оптимизировать задача Live Editor и командная строка позволяют вам формулировать и решать проблемы, и они дают идентичные результаты. Командная строка более оптимизирована, но обеспечивает меньше справки для выбора решателя, подготовки проблема и выбора опций, таких как функции построения графика. Можно также запустить, использование задач Оптимизируют, и затем генерируют код для использования командной строки, когда в Решают Ограниченную Нелинейную задачу, Основанную на решателе.
Можно просмотреть эту проблему другими способами. Следующая фигура содержит график кривых уровня этих двух целевых функций, граница Парето, вычисленная gamultiobj (поля) и x-значения истинной границы Парето (ромбы, соединенные почти прямой линией). Истинные пограничные точки Парето - то, где кривые уровня целевых функций параллельны. Алгоритм вычисляет эти точки путем нахождения, где градиенты целевых функций параллельны. Фигура построена в пространстве параметров; см. рисунок 9-1, Сопоставляющий от Пространства параметров в Пробел Целевой функции.
Контуры целевых функций и граница Парето

gamultiobj находит концы линейного сегмента, означая, что он находит в полной мере границу Парето.