Основная цель навигации состоит в том, чтобы определить в данный момент, как перейти к вашему месту назначения, избежав опасностей на пути. Первый шаг в выполнении этого должен установить ваше текущее положение. Ранние моряки остались в рамках вида земли, чтобы упростить это. Сегодня, навигация в пределах видимости (или радарная область значений) земли называется, ведя. Положения фиксируются путем корреляции подшипников и/или областей значений ориентиров. В реальном макетировании все подшипники наблюдения обработаны как локсодромы, в то время как на самом деле они - на самом деле большие круги.
По расстояниям, связанным с визуальными наблюдениями (до 20 или 30 морских миль), это предположение не вызывает измеримой ошибки, и оно обеспечивает значительное преимущество разрешения навигатору построить все подшипники как прямые линии на Меркаторской проекции.
Меркаторское было спроектировано точно с этой целью. Круги области значений, которые могут быть определены с радаром, приняты, чтобы построить как истинные круги на Меркаторском графике. Это позволяет навигатору вручную чертить дугу области значений с компасом.
Эти предположения также приводят к в вычислительном отношении эффективным методам для фиксации положений с компьютером. Тулбокс включает navfix функция, которая подражает руководству строящий и фиксирующий процесс с помощью этих предположений.
Чтобы получить хорошую навигационную фиксацию, ваше отношение по крайней мере к трем известным точкам рассматривается необходимым. Сомнительная или плохая фиксация может быть получена с двумя известными точками.
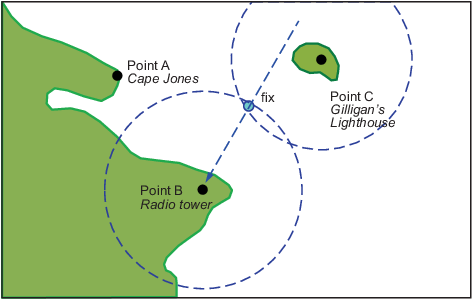
В этом мнимом прибрежном районе вы берете визуальное влияние на радиомачту 270 °. В то же время Маяк Джиллигэна переносит 0 °. Если вы строите 90 графиков на °-270 ° через радиомачту и 0 линий на °-180 ° через маяк на вашем Меркаторском графике, точке, в которой крест линий является фиксацией. Поскольку вы использовали только две линии, однако, его качество сомнительно.
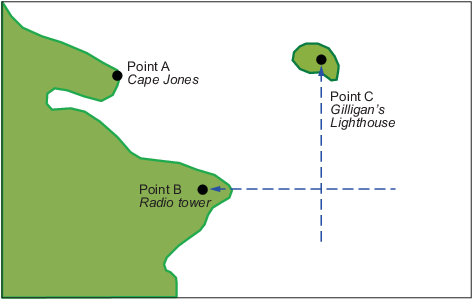
Но ожидайте; ваше наблюдение порта говорит, что он ориентировался на Мысе Джонс 300 °. Если та линия точно пересечет точку пересечения первых двух линий, у вас будет совершенная фиксация.
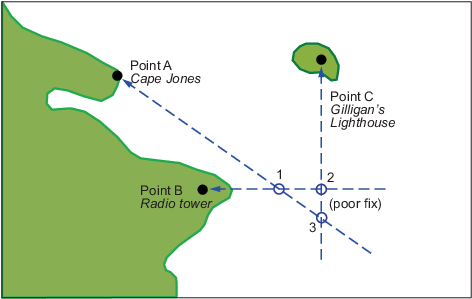
Возгласы. Что произошло? Ваше наблюдение по ошибке? Возможно, но возможно один или оба из ваших подшипников был немного по ошибке. Это происходит все время. То, которые указывают, 1, 2, или 3, правильно? Насколько вы знаете, они все одинаково допустимы.
На практике мало треугольника построено, и позиция фиксации занята или как центр треугольника или как вершина, самая близкая к опасности (как вода мелководья). Если треугольник является большим, о качестве сообщают как плохом, или как раз когда никакие не фиксируют. Если четвертая линия подшипника доступна, это может быть построено, чтобы попытаться разрешить неоднозначность. Когда все три линии, кажется, пересекаются в точно той же точке, о качестве сообщают как превосходном или совершенном.
Заметьте, что три линии привели к трем точкам пересечения. Четыре линии возвратили бы шесть точек пересечения. Это - случай комбинаторного подсчета. Каждое пересечение соответствует выбору двух линий, чтобы пересечься из числа n линий.
В следующий раз, когда вы пересекаете эти проливы, это - очень туманное утро. Вы не видите ориентиров, но к счастью, ваш навигационный радар действует. Каждый из этих ориентиров имеет хорошую радарную подпись, таким образом, вы не волнуетесь. Вы получаете диапазон от радиомачты 14 морских миль и диапазон от маяка 15 морских миль.
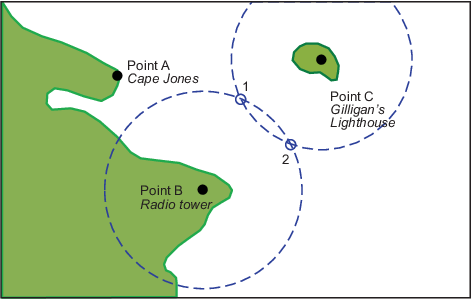
Теперь, что? Вы взяли диапазоны только от двух объектов, и все же у вас есть два возможных положения. Эта неоднозначность является результатом того, что круги могут пересечься дважды.
К счастью, ваш радар смотрят отчеты, что у него есть Мыс Джонс на уровне 18 морских миль. Это должно разрешить все.
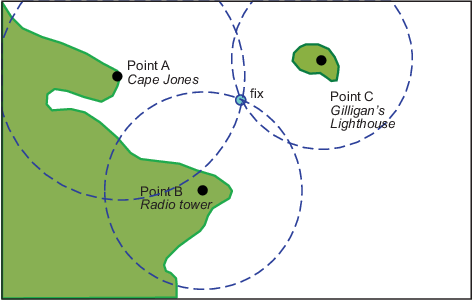
Вы были удачливы на этот раз. Третья область значений разрешила неоднозначность и дала вам превосходную фиксацию. Практически совпадают три пересечения. Иногда неоднозначность разрешена, но фиксация все еще плоха, потому что три самых близких пересечения формируют своего рода круговой треугольник.
Иногда третья область значений только добавляет к беспорядку, или путем деления пополам исходных двух вариантов, или не удаваясь пересечься один или обе из других дуг вообще. В общем случае, когда дуги n используются, 2x(n-choose-2) возможный перекрестный результат. В этом примере легко сказать, которые являются правильными.
Подшипник линий и дуг может быть объединен. Если вместо того, чтобы сообщить о третьей области значений, ваш радар смотрит, сообщил подшипник из радарной башни 20 °, неоднозначность, возможно, также была разрешена. Обратите внимание, однако, что на практике, линии подшипника для навигационной фиксации должны только проводиться визуально, кроме отчаяния. Ширина луча радара может быть степенью или больше, ведя к неопределенности.
Когда вы начинаете задаваться вопросом, мог ли этот ручной процесс графического вывода быть автоматизирован, ваш первый чиновник обнаруживается на мосту с программным обеспечением Mapping Toolbox™ и ноутбуком.
navfix navfix функция может использоваться, чтобы определить точки пересечения среди любого количества линий и дуг. Предупредите, однако, что из-за комбинаторной природы этого процесса, время вычисления растет быстро с количеством объектов. Чтобы проиллюстрировать эту функцию, присвойте положения ориентирам. Точка A, Мыс Джонс, в (latA, lonA). Точка B, радиомачта, в (latB, lonB). Точка C, Маяк Джиллигэна, в (latC, lonC).
Для линий подшипника только пример, синтаксис:
[latfix,lonfix] = navfix([latA latB latC],[lonA lonB lonC],...
[300 270 0])Это задает три точки и их подшипники, как взято из поставки. Выходные параметры выглядели бы примерно так, с фактическими числами, конечно:
latfix = latfix1 NaN % A intersecting B latfix2 NaN % A intersecting C latfix3 NaN % B intersecting C lonfix = lonfix1 NaN % A intersecting B lonfix2 NaN % A intersecting C lonfix3 NaN % B intersecting C
Заметьте, что это матрицы 2D столбца. Второй столбец состоит из NaNs, потому что это используется только для 2D перекрестной неоднозначности, сопоставленной с дугами.
Для дуг области значений только пример, синтаксис
[latfix,lonfix] = navfix([latA latB latC],[lonA lonB lonC],...
[16 14 15],[0 0 0])Это задает три точки и их области значений, как взято из поставки. Итоговый аргумент указывает, что эти три случая являются всеми областями значений.
Выходные параметры имеют следующую форму:
latfix = latfix11 latfix12 % A intersecting B latfix21 latfix22 % A intersecting C latfix31 latfix32 % B intersecting C lonfix = lonfix11 lonfix12 % A intersecting B lonfix21 lonfix22 % A intersecting C lonfix31 lonfix32 % B intersecting C
Здесь, второй столбец используется, потому что каждая пара дуг имеет два потенциальных пересечения.
Для примера подшипников и областей значений синтаксис требует, чтобы итоговый вход указал, какие объекты являются линиями подшипника (обозначенный с 1) и которые являются дугами области значений (обозначенный с 0):
[latfix,lonfix] = navfix([latB latB latC],[lonB lonB lonC],...
[20 14 15],[1 0 0])Получившийся выход смешан:
latfix = latfix11 NaN % Line B intersecting Arc B latfix21 latfix22 % Line B intersecting Arc C latfix31 latfix32 % Arc B intersecting Arc C lonfix = lonfix11 NaN % Line B intersecting Arc B lonfix21 lonfix22 % Line B intersecting Arc C lonfix31 lonfix32 % Arc B intersecting Arc C
Только одно пересечение возвращено для линии в B с дугой о B, поскольку линия происходит в кругу и пересекает его однажды. Та же линия пересекает другой круг дважды, и следовательно это возвращает две точки. Эти два круга, взятые вместе также, возвращают две точки.
Обычно, у вас есть идея как, туда, где вы - прежде чем вы возьмете фиксацию. Например, у вас может быть положение точного расчета в течение времени фиксации (см. ниже). Если вы обеспечиваете navfix с этим предполагаемым положением это выбирает из каждой пары неоднозначных пересечений точку, самую близкую к оценке. Вот то, на что это может быть похожим:
[latfix,lonfix] = navfix([latB latB latC],[lonB lonB lonC],...
[20 14 15],[1 0 0],drlat,drlon)latfix = latfix11 % the only point latfix21 % the closer point latfix31 % the closer point lonfix = lonfix11 % the only point lonfix21 % the closer point lonfix31 % the closer point
navfixЗадайте некоторые отдельные моменты посреди Атлантического океана. Они строго произвольны; возможно, они соответствуют точкам в Атлантиде:
lata = 3.1; lona = -56.2; latb = 2.95; lonb = -55.9; latc = 3.15; lonc = -55.95;
Постройте их на Меркаторской проекции:
axesm('MapProjection','mercator','Frame','on',... 'MapLatLimit',[2.8 3.3],'MapLonLimit',[-56.3 -55.8]) plotm([lata latb latc],[lona lonb lonc],... 'LineStyle','none','Marker','pentagram',... 'MarkerEdgeColor','b','MarkerFaceColor','b',... 'MarkerSize',12)
Вот то, на что это похоже (с маркировкой и мнимыми береговыми линиями, добавленными после факта для рисунка):
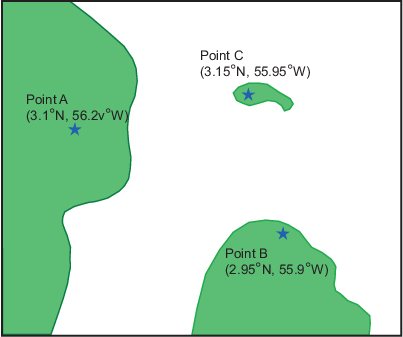
Возьмите три визуальных подшипника: Укажите переносам 289 °, Точка B переносит 135 °, и Точка C переносит 026,5 °. Вычислите пересечения:
[newlat,newlong] = navfix([lata latb latc],[lona lonb lonc],...
[289 135 26.5],[1 1 1])newlat = 3.0214 NaN 3.0340 NaN 3.0499 NaN newlong = -55.9715 NaN -56.0079 NaN -56.0000 NaN
Добавьте точки пересечения в карту:
plotm(newlat,newlong,'LineStyle','none',... 'Marker','diamond','MarkerEdgeColor','r',... 'MarkerFaceColor','r','MarkerSize',9)
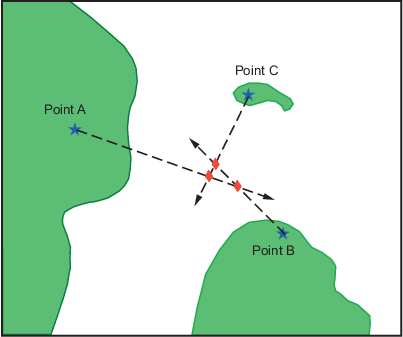
Переносящие линии были добавлены на карту в целях рисунка. Заметьте, что каждая пара результатов объектов только в одном пересечении, поскольку все - линии подшипника.
Что, если вместо этого, у вас были диапазоны от трех точек, A, B, и C, 13 морских миль, 9 морских миль и 7,5 морских миль, соответственно?
[newlat,newlong] = navfix([lata latb latc],[lona lonb lonc],...
[13 9 7.5],[0 0 0])newlat = 3.0739 2.9434 3.2413 3.0329 3.0443 3.0880 newlong = -55.9846 -56.0501 -56.0355 -55.9937 -56.0168 -55.8413
Вот то, на что похожи эти точки:
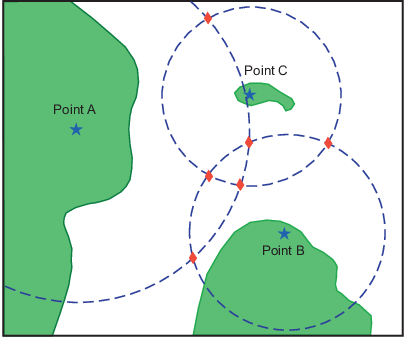
Три из этих точек выглядят разумными, три не делают.
Что, если вместо диапазона от Точки A у вас был подшипник к нему 284 °?
[newlat,newlong] = navfix([lata latb latc],[lona lonb lonc],...
[284 9 7.5],[1 0 0])newlat = 3.0526 2.9892 3.0592 3.0295 3.0443 3.0880 newlong = -56.0096 -55.7550 -56.0360 -55.9168 -56.0168 -55.8413
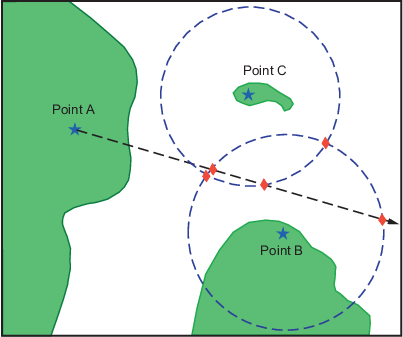
Снова, визуальный осмотр результатов указывает, который три из шести возможных точек походят на разумные положения.
При использовании положения точного расчета (3.05°N, 56.0°W), выбран более близкий, более разумный кандидат от каждой пары пересечения объектов:
drlat = 3.05; drlon = -56;
[newlat,newlong] = navfix([lata latb latc],[lona lonb lonc],...
[284 9 7.5],[1 0 0],drlat,drlon)newlat = 3.0526 3.0592 3.0443 newlong = -56.0096 -56.0360 -56.0168