fmincon РешательВ этом примере показано, как использовать Оптимизировать задачу Live Editor с fmincon решатель, чтобы минимизировать уравнение второй степени к линейным и нелинейным ограничениям и границам.
Считайте задачу нахождения [x 1, x 2], который решает
удовлетворяющее ограничениям
Начальная точка x0 поскольку этой проблемой является x 1 = 3 и x 2 = 1.
Создайте новый live скрипт путем нажатия кнопки New Live Script в разделе File по вкладке Home.
Вставьте Оптимизировать задачу Live Editor. Кликните по вкладке Insert и затем, в разделе Code, выберите Task > Optimize.
Для дальнейшего использования во вводе проблемных данных выберите Insert > Section Break. Новые разделы появляются выше и ниже задачи.
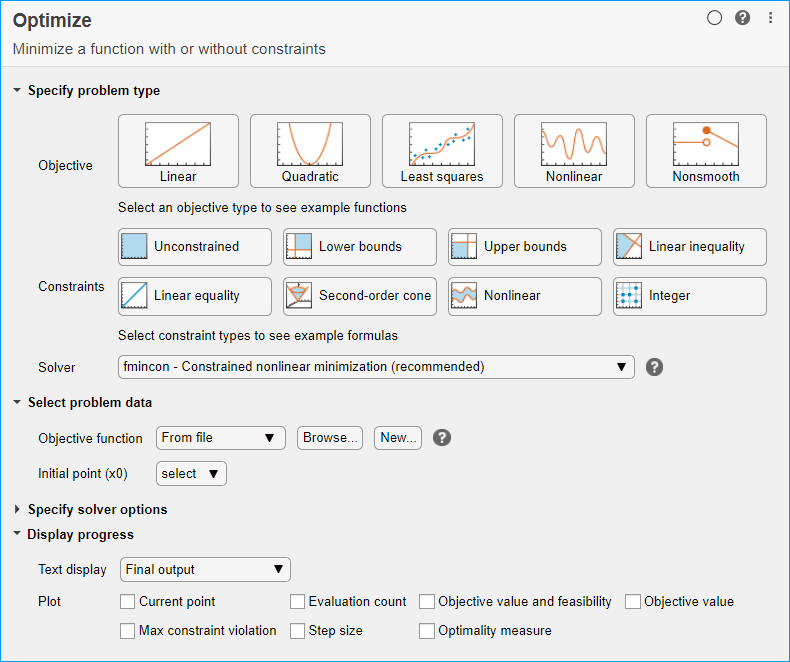
При запуске с верхней части задачи введите проблемный тип и типы ограничения. Нажмите кнопку Objective > Quadratic и Constraints > Lower bounds, Linear inequality и кнопки Nonlinear. Задача показывает, что рекомендуемый решатель fmincon.
Целевая функция
Целевая функция достаточно проста представлять как анонимная функция. Расположите курсор в раздел выше задачи и введите этот код.
fun = @(x)sum(x.^2);
Нижняя граница
Проблема содержит нижнюю границу x 1 ≥ 0.5. Опишите это связало как переменная lb. С курсором в конце линии, задающей целевую функцию, нажмите Enter и введите следующий код, чтобы задать нижнюю границу.
lb = [0.5 -Inf];
Начальная точка
С курсором в конце линии, задающей нижнюю границу, нажмите Enter и введите следующий код, чтобы установить начальную точку.
x0 = [3,1];
Линейное ограничение
С курсором в конце линии, задающей начальную точку, нажмите Enter и введите следующий код, чтобы установить линейное ограничение.
A = [-1,-1]; b = -1;
Запустите раздел
Главный раздел теперь включает пять параметров.
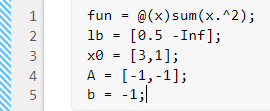
Затем необходимо запустить раздел, чтобы поместить параметры в рабочую область как переменные. Для этого кликните по крайней левой области раздела, который содержит панель диагональных дорожек. После того, как вы кликаете по этой области, панель становится твердой панелью, указывая, что переменные находятся теперь в рабочей области. (Примечание: можно также нажать Ctrl+Enter, чтобы запустить раздел.)
Установите проблемные данные
Введите переменные в раздел Select problem data задачи. Чтобы задать целевую функцию, выберите Objective function > Function handle и выберите fun.
Установите начальную точку x0.
Выберите Lower bounds > From workspace и выберите lb.
Установите линейные переменные A ограничения неравенства и b в области Linear inequality.
Теперь задайте нелинейные ограничения неравенства. В разделе Select problem data выберите Nonlinear > Local function, и затем нажмите кнопку New. Функция появляется в новом разделе ниже задачи. Отредактируйте получившийся код, чтобы содержать следующие непрокомментированные линии.
function [c,ceq] = constraintFcn(x) % You can include commented code lines or not. % Be sure that just these uncommented lines remain: c = [-x(1)^2 - x(2)^2 + 1; -9*x(1)^2 - x(2)^2 + 9; -x(1)^2 + x(2); -x(2)^2 + x(1)]; ceq = []; end
В разделе Select problem data выберите функцию constraintFcn.
Контролируйте прогресс
В разделе Display progress задачи выберите Text display > Each iteration, таким образом, можно контролировать прогресс решателя. Выберите Objective value для графика.
Ваша настройка выглядит так:
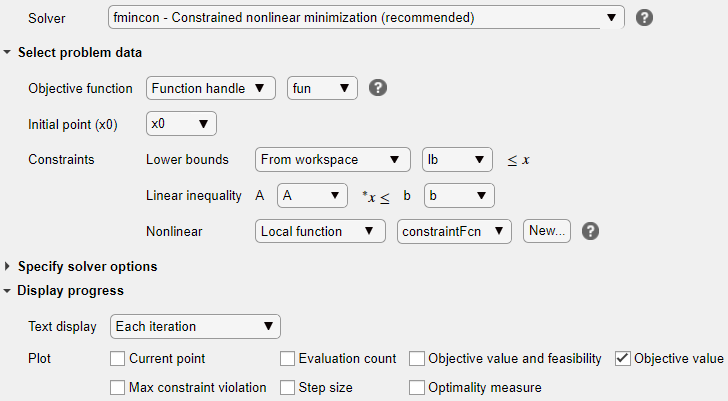
Чтобы запустить решатель, кликните по кнопке ⁝ опций в правом верхнем из окна задачи и выберите Run Section.
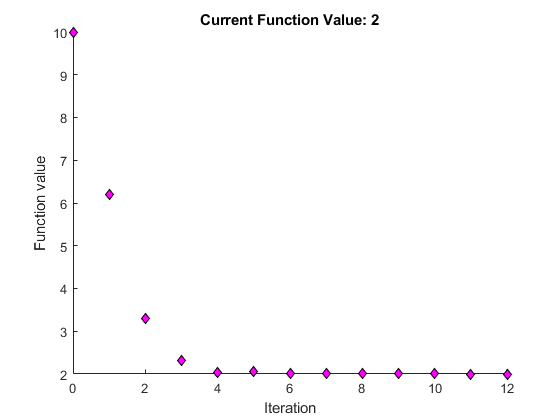
График появляется в отдельном окне рисунка и в области вывода задачи.
Чтобы видеть, куда переменные решения возвращены, посмотрите во главе задачи.
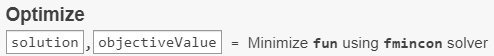
Конечная точка и ее связанное значение целевой функции появляются в solution и objectiveValue переменные в рабочей области. Просмотрите эти значения путем ввода этого кода в разделе Live Editor ниже задачи.
solution, objectiveValue
Нажмите Ctrl+Enter, чтобы запустить раздел.
![solution = [1 1], objectiveValue = 2](optimizelet_fmincon_answer.png)