Решите следующую задачу теплопередачи различными материальными параметрами. Этот пример использует приложение PDE Modeler. Для командной строки решения видят Теплопередачу Между Двумя Квадратами, Сделанными из Различных Материалов.
2D геометрия для этой проблемы является квадратом со встроенным ромбом (квадрат с 45 вращениями степеней). УЧП, управляющий этой проблемой, является параболическим уравнением тепла:
где ρ является плотностью, C является теплоемкостью, k является коэффициентом проводимости тепла, Q является источником тепла, h является конвективным коэффициентом теплопередачи, и расширение T является внешней температурой.
Чтобы решить эту задачу в приложении PDE Modeler, выполните эти шаги:
Смоделируйте геометрию: чертите квадратную область с углами в (0,0), (3,0), (3,3), и (0,3) и ромбовидную область с углами в (1.5 0.5), (2.5 1.5), (1.5 2.5), и (0.5 1.5).
pderect([0 3 0 3]) pdepoly([1.5 2.5 1.5 0.5],[0.5 1.5 2.5 1.5])
Установите x - предел по осям [-1.5 4.5] и y - предел по осям [-0.5 3.5]. Для этого выберите Options> Axes Limits и установите соответствующие области значений.
Установите режим приложения на Heat Transfer.
Температура сохранена в 0 на всех внешних границах, таким образом, вы не должны изменять значение по умолчанию граничное условие Дирихле T = 0.
Задайте коэффициенты. Для этого выберите PDE> PDE Mode. Затем кликните по каждой области и выберите PDE> PDE Specification или нажмите кнопку PDE на панели инструментов. Поскольку вы решаете параболическое уравнение тепла, выберите тип Parabolic УЧП для обеих областей. Для квадратной области задайте следующие коэффициенты:
Плотность, pho = 2
Теплоемкость, C = 0.1
Коэффициент проводимости тепла, k = 10
Источник тепла, Q = 0
Конвективный коэффициент теплопередачи, h = 0
Внешняя температура, Text = 0
Для ромбовидной области задайте следующие коэффициенты:
Плотность, pho = 1
Теплоемкость, C = 0.1
Коэффициент проводимости тепла, k = 2
Источник тепла, Q = 4
Конвективный коэффициент теплопередачи, h = 0
Внешняя температура, Text = 0
Инициализируйте mesh путем выбора Mesh> Initialize Mesh. Для более точного решения совершенствуйте mesh путем выбора Mesh> Refine Mesh.
Установите начальное значение и время решения. Для этого выберите Solve> Parameters.
Динамика для этой проблемы очень быстра — температура достигает устойчивого состояния приблизительно в 0,1 единицах измерения времени. Чтобы получить интересную часть динамики, установите время на logspace(-2,-1,10). Это дает 10 логарифмически расположенных с интервалами чисел между 0,01 и 0.1. Установите начальное значение температурного u (t 0) к 0.
Решите уравнение путем выбора Solve> Solve PDE или нажатия кнопки = на панели инструментов.
Постройте решение. По умолчанию приложение строит температурное распределение в прошлый раз. Лучший способ визуализировать динамическое поведение температуры состоит в том, чтобы анимировать решение. Для этого выберите Plot> Parameters и выберите Animation и опции Height (3-D plot), чтобы анимировать 3-D график. Кроме того, можно выбрать опцию Plot in x-y grid, чтобы использовать прямоугольную сетку вместо треугольной сетки по умолчанию. Используя прямоугольную сетку вместо треугольной сетки значительно ускоряет процесс анимации.
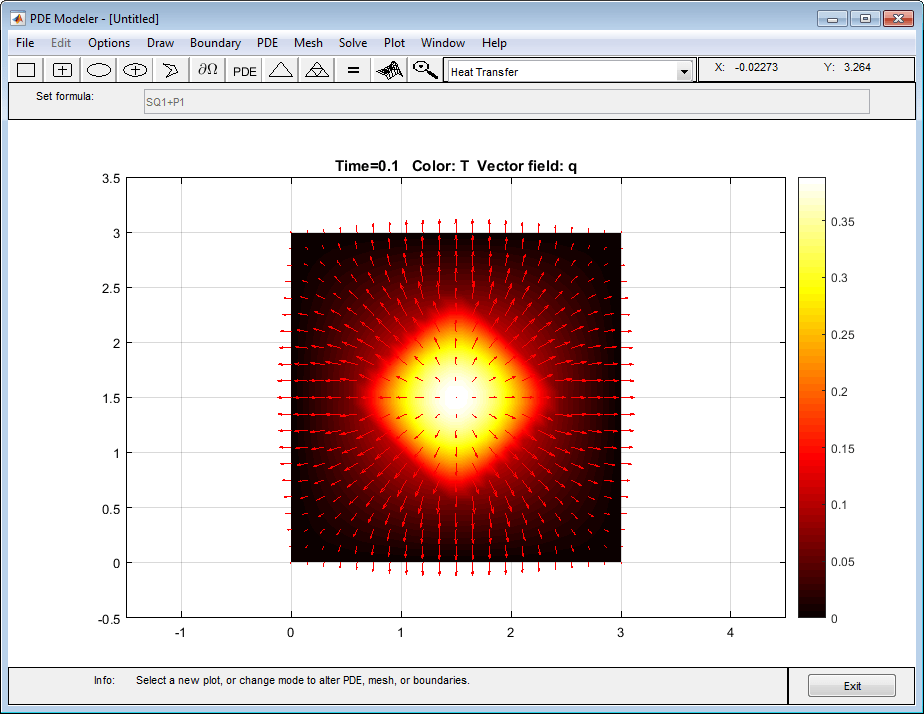
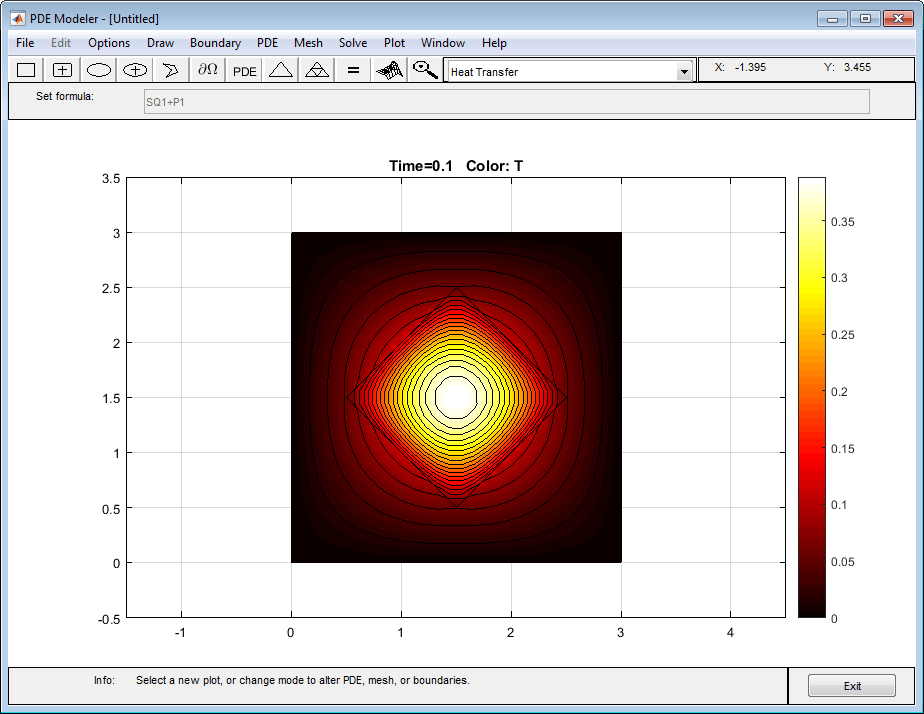
Можно также построить изотермические графики с помощью контурного графика и потока тепла векторное поле с помощью стрел.
Выберите Plot> Parameters.
В получившемся диалоговом окне отмените выбор Animation, и Height (3-D plot) и опций Plot in x-y grid.
Измените палитру в hot при помощи соответствующего выпадающего меню в том же диалоговом окне.
Чтобы получить первый график, выберите опции Contour и Color.
Для второго графика выберите Color и Arrows и установите их значения к temperature и heat flux, соответственно.
Изотермические линии
Температура и поток тепла