Номинальная стоимость обеспечивает способ задать ожидаемую величину переменной в модели, похожей на определение оценки трансформатора или установку области значений на вольтметре. В этом примере показано, как можно подстроить масштабирование отдельных переменных в модели, чтобы улучшать производительность решателя и увеличить сходимость моделирования.
Когда решатель выполняет числовую симуляцию и анализ, это использует переменные без модулей. Номинальная стоимость является способом преобразовать технические переменные с модулями в переменные без модулей и масштабировать их для оптимальной эффективности решателя. Номинальная стоимость имеет значение с модулем, и этот модуль используется, чтобы снять модуль для числовых вычислений. Номинальная стоимость затем определяет величину переменной, как замечено числовыми алгоритмами. Это обычно выгодно, чтобы иметь величины подобной шкалы.
Рассмотрите простую модель массового пружинного демпфера с большим коэффициентом упругости.
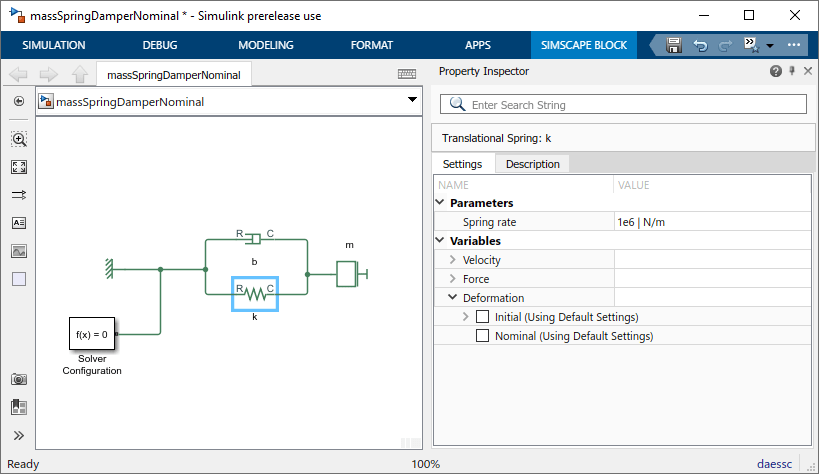
Модель использует настройки параметров блоков по умолчанию, за исключением коэффициента упругости:
Коэффициент упругости, k = 1e6 N/m
Коэффициент демпфирования, b = 100 Н / (m/s)
Масса, m = 1 кг
Начальная массовая скоростная переменная, v, имеет High приоритет и начальное целевое значение 0,1 м/с. Модель использует номинальную стоимость по умолчанию с m как единица длины.
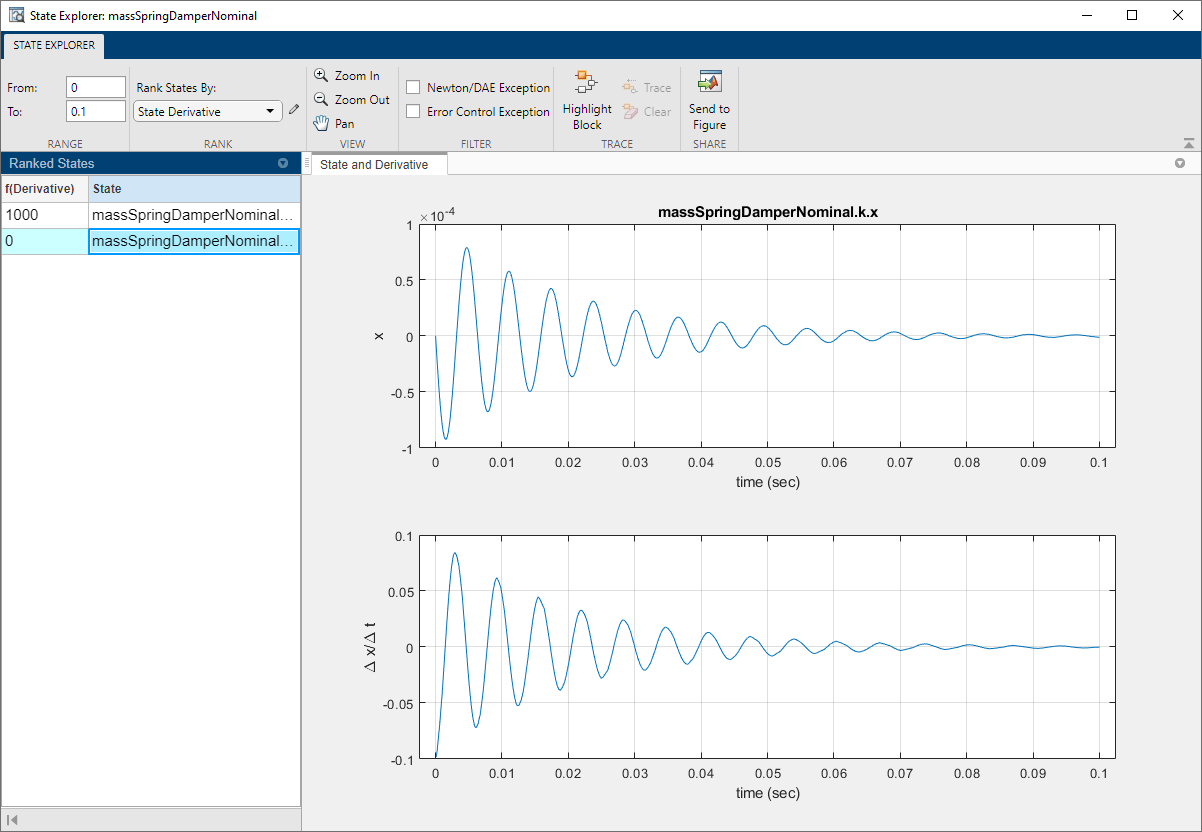
Когда вы симулируете эту модель, пружинный Deformation (положение), переменная x мала, в 10^-5 м области значений.
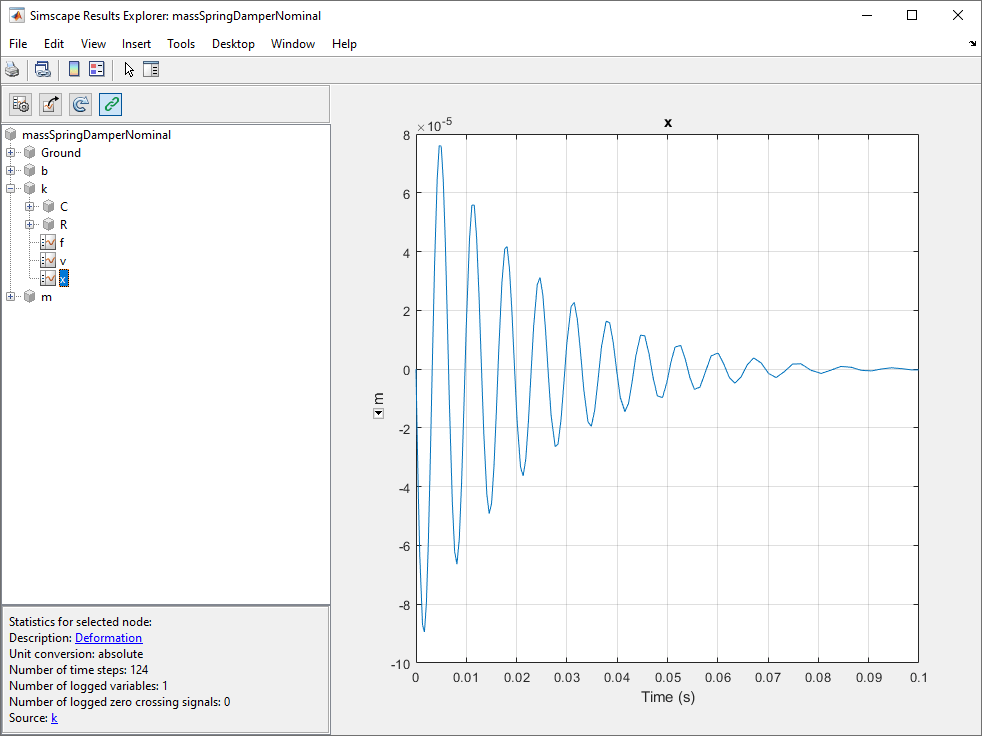
Откройте Solver Profiler путем нажатия на гиперссылку в нижнем правом углу окна модели.
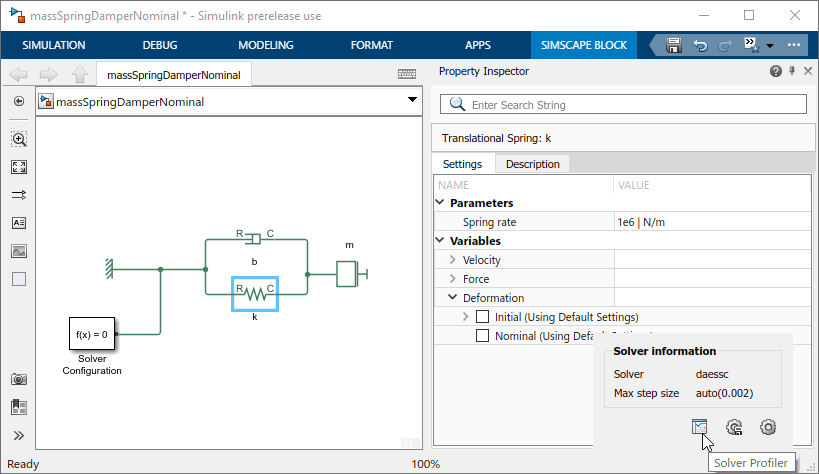
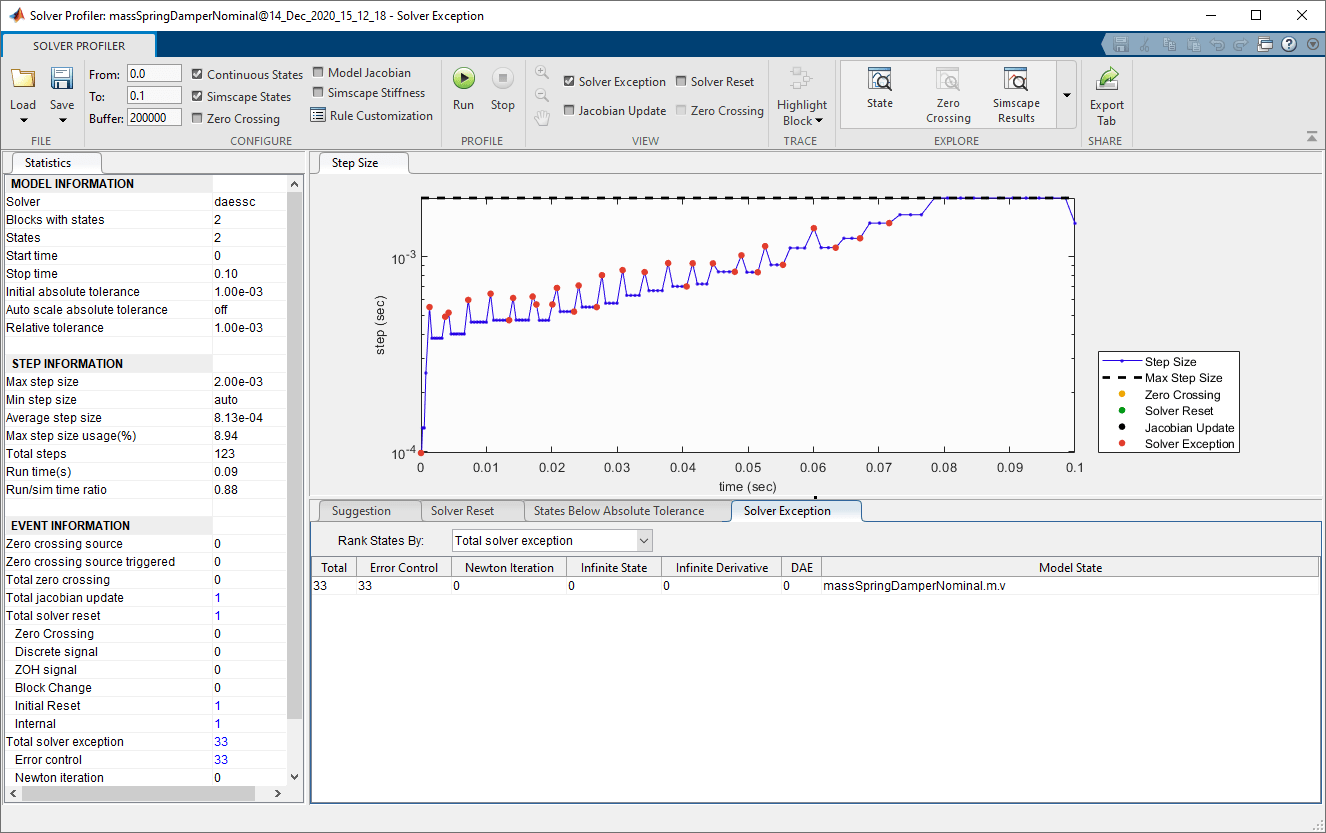
Решатель полностью игнорирует переменную положения и только смотрит на скоростную переменную. Числовая величина положения ниже допуска к той переменной.
Средство просмотра состояния, к которому получают доступ от панели инструментов Solver Profiler, показывает величину каждой переменной, как замечено решателями.
Ситуация ясна, если мы смотрим на уравнения модели:
Когда k является очень большим, по сравнению с m и b, затем x мал, так, чтобы продукт k *x имел разумный размер, по сравнению с другими условиями в уравнении. Чтобы исправить ситуацию, мы должны масштабировать x. Другими словами, мы должны выбрать номинальную стоимость для x, который мал, так, чтобы масштабированная переменная, x s, стала более довольно размерной:
где c является большим. Например, если номинальная стоимость является 1 μm, и исходный x находится в m, то c 1e6. Уравнения затем становятся:
и условия имеют величины подобной шкалы.
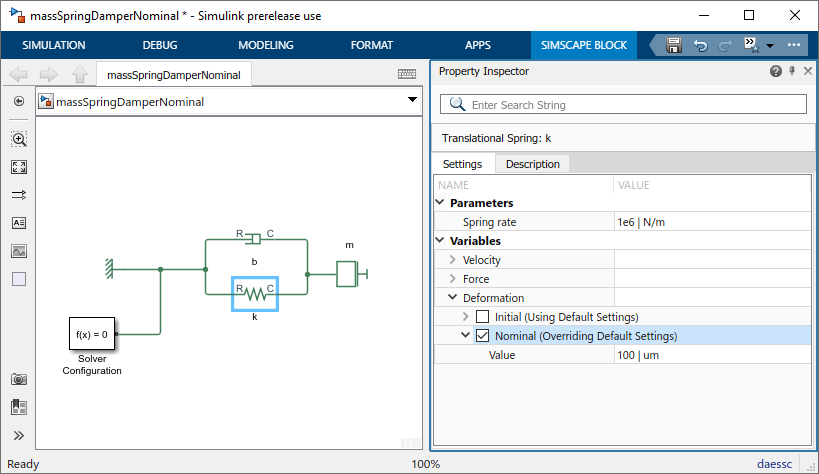
Давайте применим этот принцип масштабирования к переменным модели. Во-первых, используйте Property Inspector, чтобы изменить номинальную стоимость пружинной переменной Deformation, x, к 100 um (1e-4 m).
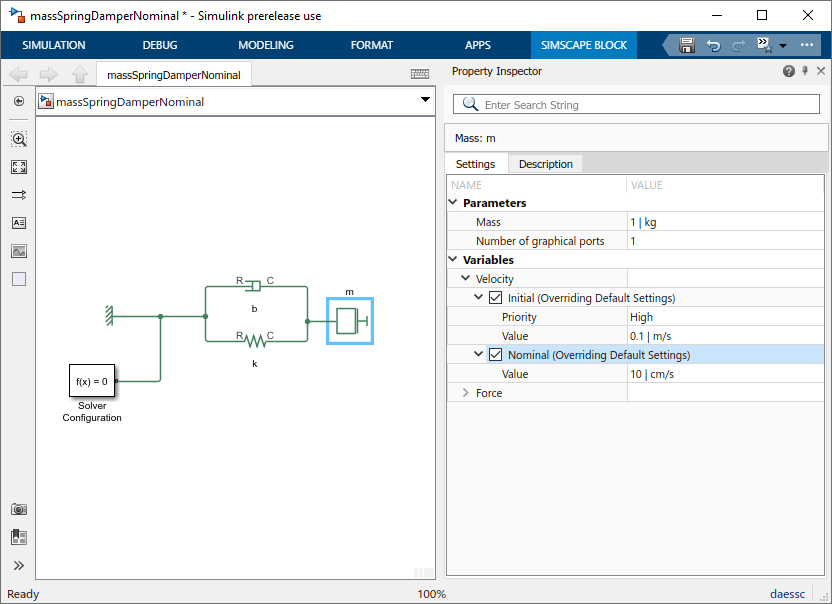
Точно так же измените номинальную стоимость массовой переменной Velocity к 10 см/с (0,1 м/с).
Это приносит шкалу величины обеих переменных, замеченных решателем к приблизительно 1.
Повторно выполните симуляцию.
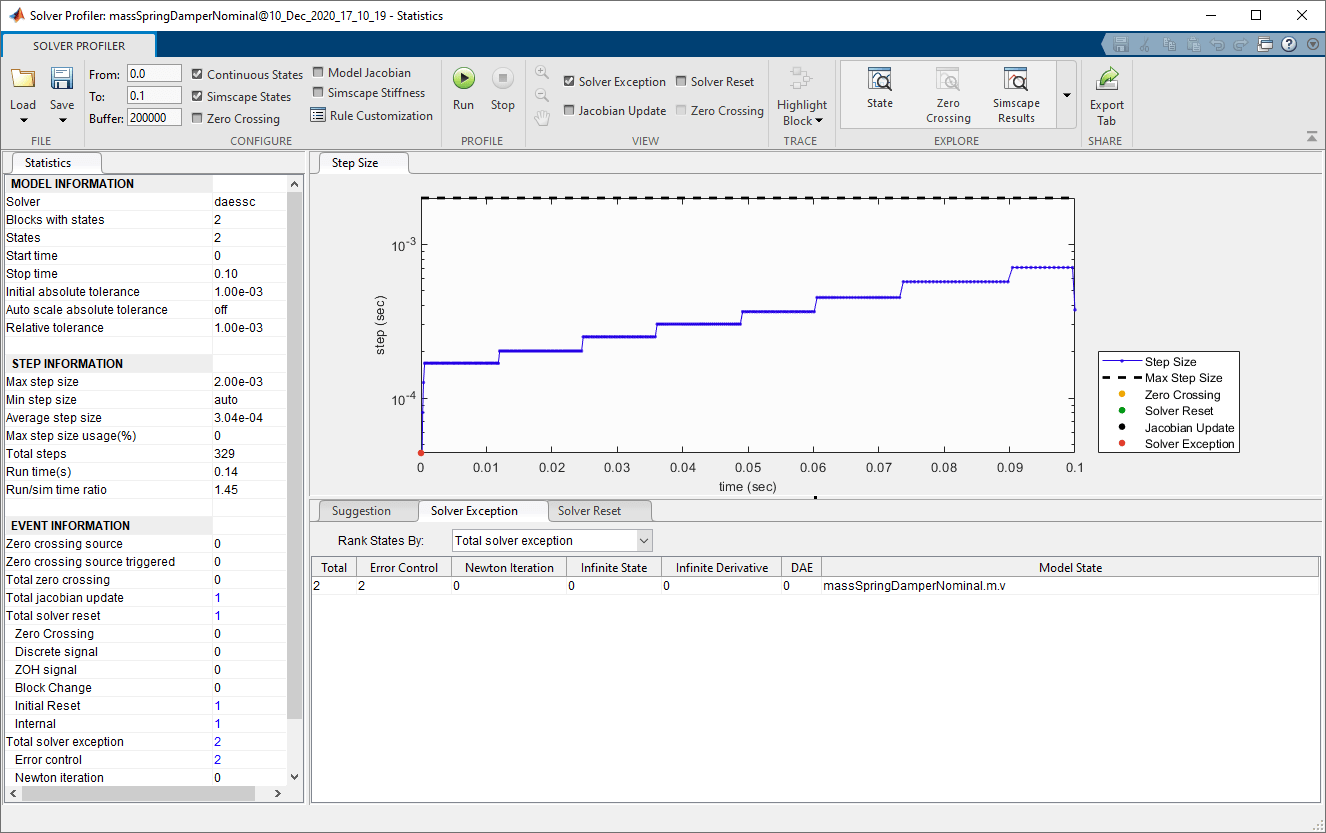
Существует теперь только два исключения решателя, в начале симуляции.
Обратите внимание на то, что эффективная абсолютная погрешность теперь более трудна для массовой скорости. Эффективная абсолютная погрешность для моделей Simscape™ имеет модуль и вычисляется как (номинальная стоимость * глобальный AbsTol без модулей). В первой симуляции запускается, эффективная абсолютная погрешность была 1e-3 м/с, и теперь это - 1e-4 м/с, потому что номинальная стоимость изменила величину и глобальный AbsTol все еще 1e-3. Однако скорость симуляции подобна, даже с увеличенным AbsTol на массовой скорости и увеличенных временных шагах.
Значения, как замечено решателем, подобны в величине и для переменных скорости и для положения.
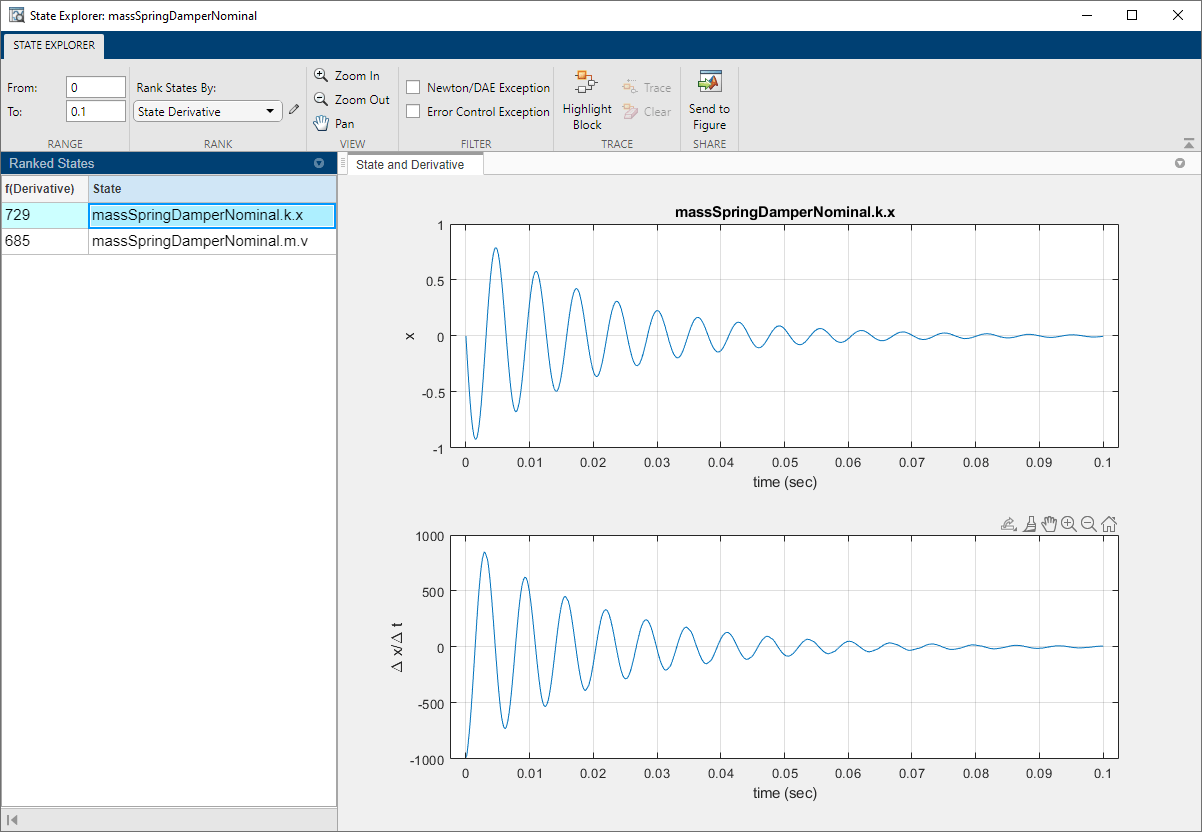
Теперь измените глобальный AbsTol к 1e-2, более тесно совпадать с точностью скоростной переменной во время первой запущенной симуляции.
Повторно выполните симуляцию.
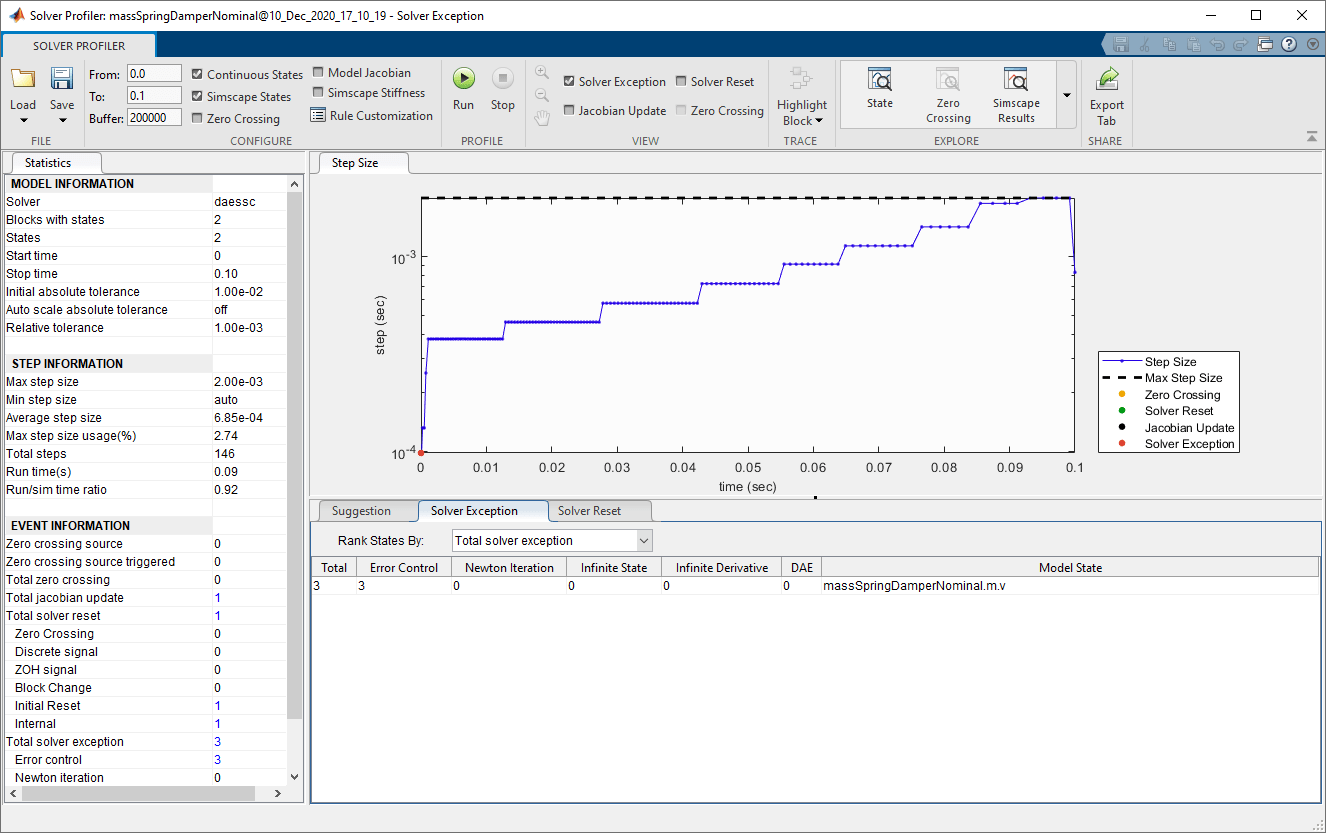
Такты подобны, и количество исключений равняется 3 также в начале моделирования.