Выбор системы координат измерения

Можно использовать блок Transform Sensor, чтобы измерить относительное отношение между двумя произвольными системами координат, которые соединяются с B и портами системы координат F блока. Отношение включает относительное вращение, перевод и их производные первого и второго раза. Эти измерения являются 3-D векторами или выше определенными размеры количествами, такими как матрицы вращения.

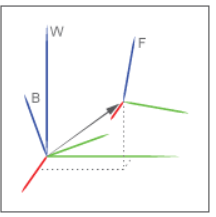
Чтобы сделать расчет с измеренными векторами, векторы должны быть разрешены в координатах. Установка параметра Measurement Frame определяет, где разрешить измеренные векторы; векторы разрешены в координатах выбранной системы координат. Например, на рисунке, потому что Measurement Frame был установлен в World, блок Transform Sensor разрешает вектор сдвига, показавший черной стрелой, в координатах мировой системы координат.

Примечание

Измерение вращения блока Transform Sensor независимо от параметра Measurement Frame.

Система координат измерения

Можно установить параметр Measurement Frame на World, Base, Follower, Non-Rotating Base, и Non-Rotating Follower.

`World`

Блок Transform Sensor разрешает измеренные векторы в координатах мировой системы координат.

Мировая система координат является инерционной системой координат.

`Base` или `Follower`

Блок Transform Sensor разрешает измеренные векторы в координатах выбранной системы координат, которая является системой координат последователя или основой.

Система координат основы или последователя является системой координат, которая соединяется с портом B или F блока, соответственно. База и последующая система координат является неинерционной. Поэтому векторы, разрешенные в основе или системе координат последователя, могут включить центростремительные и Кориолисовы условия.

`Non-Rotating Base` или `Non-Rotating Base`

Блок-диаграммы Transform Sensor векторы, разрешенные в мировой системе координат к выбранной системе координат, которая не вращает основу или не вращает систему координат последователя. Другими словами, блок вычисляет матрицу вращения от мировой системы координат до текущей основы, или система координат последователя затем умножает матрицу с векторами, разрешенными в мировой системе координат.

Не вращающаяся основа или не вращающаяся система координат последователя являются мгновенной системой координат, которая является совпадающей и выравнивается с соответствующей основой или системой координат последователя в текущее время. Измерения, разрешенные в невращающихся системах координат, не включают центростремительные и Кориолисовы условия.

Таблица сравнивает свойства измерений для различных настроек Measurement Frame.

Система координат измерения	Стандартное производное отношение
Мир	Да
Основа	Да
Последователь	Да
Невращение основы	Нет
Невращение последователя	Нет

Когда выбранная система координат удовлетворяет стандартному производному отношению, измерения, разрешенные в этой системе координат, связаны друг с другом. Например, когда вы выбираете World, разрешенный линейный ускоряющий вектор является производной времени разрешенного линейного вектора скорости, который является производной времени разрешенного линейного вектора сдвига.

Пример

Этот пример показывает измерения блока Transform Sensor с различными настройками параметра Measurement Frame. Изображение иллюстрирует одну систему степени свободы с четырьмя частями: поддержка, концентратор, стержень и автомобиль. Поддержка закрепляется на земле, и стержень соединяет концентратор и автомобиль. Основа, последователь и мировые системы координат системы расположены в центре концентратора, автомобиля и нижней части поддержки, соответственно.

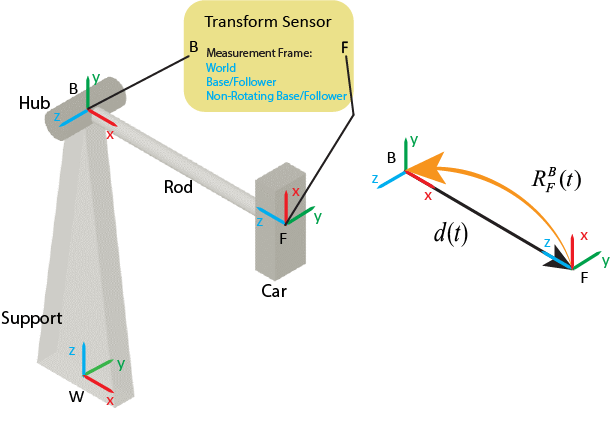
Single DoF System

Стержень имеет длину $r$ и вращается с постоянной угловой скоростью, $ω$ , вокруг Z- ось базовой системы координат. Блок Transform Sensor используется, чтобы измерить относительные движения между автомобилем и концентратором. Например, блок измеряет относительный перевод, $d (t)$ и вращение, $R_{F}^{B} (t)$ между автомобилем и концентратором.

Изображение показывает вид спереди системы. В целях простоты этот пример только показывает, как разрешить линейные измерения, такие как перевод, скорость и ускорение, в Декартовых координатах.

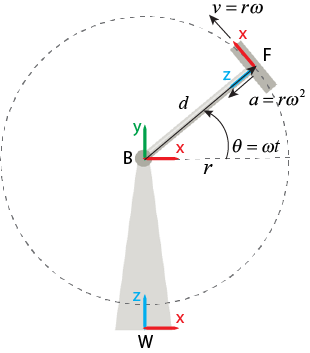
System Front View

`World`

Когда вы устанавливаете Measurement Frame на World, блок измеряется, движение системы координат последователя относительно базовой системы координат затем разрешает относительное движение в мировой системе координат.

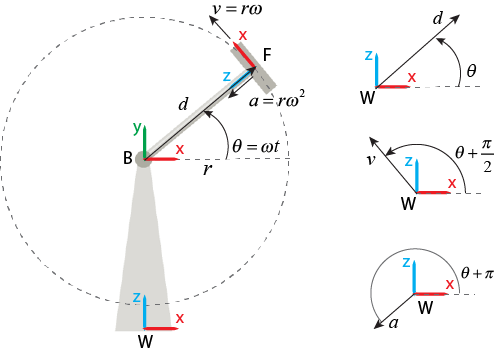
Example Word Frame

Перевод, скорость и ускоряющие векторы имеют постоянные величины, потому что длина стержня является постоянной. Однако они вращаются с постоянной вращательной скоростью, $ω$ , вокруг Y- ось мировой системы координат. Поэтому перевод, скорость и ускоряющие векторы могут быть описаны как:

$d_{w} (t) = r [\begin{matrix} \cos ω t \\ 0 \\ \sin ω t \end{matrix}]$

$v_{w} (t) = r ω [\begin{matrix} - \sin ω t \\ 0 \\ \cos ω t \end{matrix}]$

$a_{w} (t) = r ω^{2} [\begin{matrix} - \cos ω t \\ 0 \\ - \sin ω t \end{matrix}]$

Обратите внимание на то, что векторы, разрешенные в мировой системе координат всегда, удовлетворяют стандартному производному отношению. Например, $a_{w}$ равняется производной времени $v_{w}$ .

`Base` или `Follower`

Когда вы устанавливаете Measurement Frame на Base, блок измеряет относительное движение системы координат последователя относительно базовой системы координат и разрешает измерения в координатах базовой системы координат.

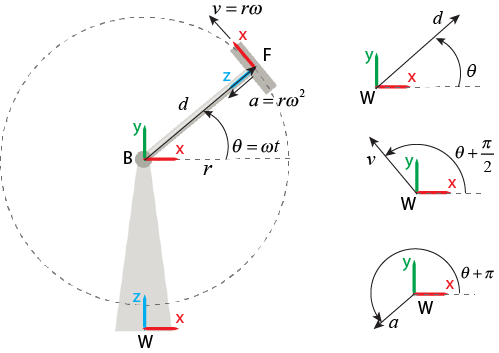
Example Base Frame

Поскольку базовая система координат фиксируется в этом примере, измерения могут быть описаны как:

$d_{b} (t) = r [\begin{matrix} \cos ω t \\ \sin ω t \\ 0 \end{matrix}]$

$v_{b} (t) = r ω [\begin{matrix} - \sin ω t \\ \cos ω t \\ 0 \end{matrix}]$

$a_{b} (t) = r ω^{2} [\begin{matrix} - \cos ω t \\ - \sin ω t \\ 0 \end{matrix}]$

Когда вы устанавливаете Measurement Frame на Follower, блок измеряется, относительное движение системы координат последователя к базовой системе координат затем разрешает измерения в координатах системы координат последователя. Разрешенные векторы включают центростремительные и Кориолисовы условия, потому что система координат последователя вращается в зависимости от времени. Наблюдателю, присоединенному к системе координат последователя, источник базовой системы координат никогда не перемещается. Поэтому линейная скорость и линейное ускорение являются нулем.

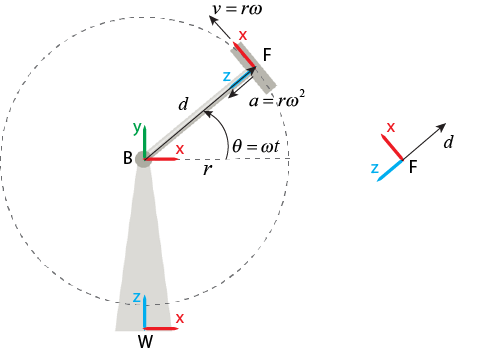
Example Follower

$d_{f} (t) = r [\begin{matrix} 0 \\ 0 \\ - 1 \end{matrix}]$

$v_{f} (t) = r ω [\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}]$

$a_{f} (t) = r ω^{2} [\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}]$

Обратите внимание на то, что векторы, разрешенные в базе и последующей системе координат всегда, удовлетворяют стандартному производному отношению. Например, $v_{b}$ равняется производной времени $d_{b}$ .

`Non-Rotating Base` или `Non-Rotating Follower`

Когда установленный Measurement Frame к Non-Rotating Base, блок-диаграммы векторы, разрешенные в мировой системе координат к мгновенной системе координат, которая является совпадающей и выравнивается с базовой системой координат в текущий момент.

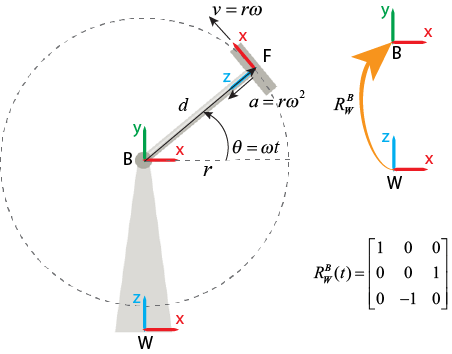
Example Non-Rotating Base

$d_{n b} (t) = R_{W}^{B} * d_{w} (t) = r [\begin{matrix} \cos ω t \\ \sin ω t \\ 0 \end{matrix}]$

$v_{n b} (t) = R_{W}^{B} * v_{w} (t) = r ω [\begin{matrix} - \sin ω t \\ \cos ω t \\ 0 \end{matrix}]$

$a_{n b} (t) = R_{W}^{B} * a_{w} (t) = r ω^{2} [\begin{matrix} - \cos ω t \\ - \sin ω t \\ 0 \end{matrix}]$

Когда вы устанавливаете Measurement Frame на Non-Rotating Follower, блок-диаграммы векторы, разрешенные в мировой системе координат к мгновенной системе координат, которая является совпадающей и выравнивается с системой координат последователя в текущий момент.

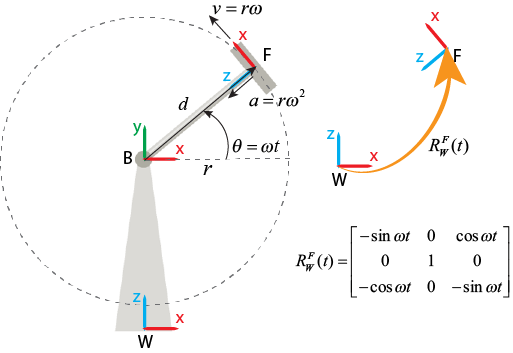
Example Non-Rotating Follower

$d_{n f} (t) = R_{W}^{F} * d_{w} (t) = r [\begin{matrix} 0 \\ 0 \\ - 1 \end{matrix}]$

$v_{n f} (t) = R_{W}^{F} * v_{w} (t) = r ω [\begin{matrix} 1 \\ 0 \\ 0 \end{matrix}]$

$a_{n f} (t) = R_{W}^{F} * a_{w} (t) = r ω^{2} [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}]$

Обратите внимание на то, что, если система координат основы или последователя не фиксируется, измерения в ее соответствующей системе координат невращения не удовлетворяют стандартному производному отношению. Например, потому что система координат последователя вращается, если вы устанавливаете Measurement Frame на Non-Rotating Follower, разрешенный вектор скорости не является производной времени разрешенного вектора сдвига.

Документация