RST Controller

Прогнозирующее управление с помощью полиномиального представления

Библиотека:
Simscape / Электрический / Управление / Общее Управление

Описание

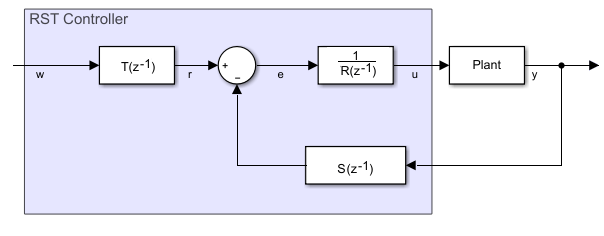
Блок RST Controller реализует обобщенный прогнозирующий контроллер, использующий опорный сигнал, отслеживающий полиномиальное представление. Схема показывает эквивалентную схему для алгоритма управления.

Уравнения

Модель управляемого авторегрессивного интегрированного скользящего среднего значения (CARIMA) описывает объект:

$A (z^{- 1}) y (k) = z^{- d} B (z^{- 1}) u (k - 1) + \frac{e (k) C (z^{- 1})}{D (z^{- 1})}$

$A (z^{- 1}) = 1 + a_{1} z^{- 1} + \dots + a_{n_{A}} z^{- n_{A}}$

$B (z^{- 1}) = b_{0} + b_{1} z^{- 1} + \dots + b_{n_{B}} z^{- n_{B}}$

$C (z^{- 1}) = 1$

$D (z^{- 1}) = 1 - z^{- 1},$

где:

d является системной потерей времени.
y(k) является объектом выход.
u(k) является контроллером выход.
e(k) является белым шумом с нулевым средним значением.
^A(z-1) и ^B(z-1) являются системными полиномами.
_nA и _nB являются степенями полиномов.
^C(z-1) и ^D(z-1) являются полиномами воздействия для получения установившейся ошибки.

Модель предсказания дана как

$\hat{y} (k + j | k) = G_{j - d} (z^{- 1}) D (z^{- 1}) z^{- d - 1} u (k + j) + \frac{H_{j - d} (z^{- 1}) D (z^{- 1})}{C (z^{- 1})} u (k - 1) + \frac{F_{j - d} (z^{- 1})}{C (z^{- 1})} y (k)$

$j = \bar{h i, h p}$

где:

hi является минимальным предсказанием.
hp является горизонтом предсказания.

Будущая управляющая последовательность, вычисленная во время k,

$u (k + j - 1 | k),$

где

$j = \bar{1, h c}$

и hc является горизонтом управления.

Ожидаемые значения выхода

$\hat{y} (k + j | k) .$

Определить системные полиномы, $F_{j - d} (z^{- 1})$ , $G_{j - d} (z^{- 1})$ , и $H_{j - d} (z^{- 1})$ , блок использует два диофантовых уравнения. Первое диофантовое уравнение

$\frac{C (z^{- 1})}{A (z^{- 1}) D (z^{- 1})} = E_{j - d} (z^{- 1}) + z^{- j + d} \frac{F_{j - d} (z^{- 1})}{A (z^{- 1}) D (z^{- 1})},$

где:

$E_{j - d} (z^{- 1}) = 1 + 1 + e_{1} z^{- 1} + \dots + e_{n_{E}} z^{- n_{E}}$

$F_{j - d} (z^{- 1}) = f_{0} + f_{1} z^{- 1} + \dots + f_{n_{F}} z^{- n_{F}}$

$n_{E} = j - d - 1$

$n_{F} = max (n_{A} + n_{D} - 1, n_{C} - j + d)$

Второе диофантовое уравнение

$E_{j - d} (z^{- 1}) B (z^{- 1}) = C (z^{- 1}) G_{j - d} (z^{- 1}) + z^{- j + d} H_{j - d} (z^{- 1}),$

где:

$G_{j - d} (z^{- 1}) = g_{0} + g_{1} z^{- 1} + \dots + g_{n_{G}} z^{- n_{G}}$

$H_{j - d} (z^{- 1}) = h_{0} + h_{1} z^{- 1} + \dots + h_{n_{H}} z^{- n_{H}}$

$n_{G} = j - d - 1$

$n_{H} = max (n_{C}, n_{B} + d) - 1$

Получившаяся модель предсказания

$\hat{y} (k + j | k) = G_{j - d} (z^{- 1}) D (z^{- 1}) z^{- d - 1} u (k + j) + {\hat{y}}_{0} (k + j | k),$

где

${\hat{y}}_{0} (k + j | k) = \frac{H_{j - d} (z^{- 1}) D (z^{- 1})}{C (z^{- 1})} u (k - 1) + \frac{F_{j - d} (z^{- 1})}{C (z^{- 1})} y (k)$

представляет свободный ответ системы.

Используя матричное обозначение, модель предсказания может быть записана как

$\hat{y} = {Gu}_{d} + {\hat{y}}_{0},$

где:

$\hat{y} = {[\hat{y} (k + h i | k), \hat{y} (k + h i + 1 | k), \dots, \hat{y} (k + h p | k)]}^{T}$

$G = [\begin{matrix} g_{h i - d - 1} & \dots & g_{0} & 0 & \dots & 0 \\ g_{h i - d} & \dots & g_{1} & g_{0} & \dots & 0 \\ \dots & \dots & \dots & \dots & \dots & \dots \\ g_{h c - 1} & \dots & \dots & \dots & \dots & g_{0} \\ g_{h p - d - 1} & \dots & \dots & \dots & \dots & g_{h p - h c - 1} \end{matrix}]$

$u_{d} = {[D (z^{- 1}) u (k), \dots, D (z^{- 1}) u (k + h c - 1)]}^{T}$

${\hat{y}}_{0} = {[{\hat{y}}_{0} (k + h i | k), {\hat{y}}_{0} (k + h i + 1 | k), \dots, {\hat{y}}_{0} (k + h p | k)]}^{T}$

Чтобы минимизировать ошибку отслеживания и контроллер выход, блок использует функцию стоимости. Чтобы обменять между минимизацией ошибки отслеживания и минимизацией контроллера выход, блок использует фактор взвешивания, λ, такой что

$J = {({Gu}_{d} + {\hat{y}}_{0} - w)}^{T} ({Gu}_{d} + {\hat{y}}_{0} - w) + λ u_{d}^{T} u_{d}$

для

$D (z^{- 1}) u (k + i) = 0$

$i \in [h c, h p - d - 1],$

где w является ссылочным вектором траектории. При минимизации функции стоимости, дает к уравнению для последовательности оптимального управления:

$u_{d}^{*} = (G^{T} G + λ I_{h c}) G^{T} [w - {\hat{y}}_{0}] .$

Как _γj и $j = \bar{h i, h p}$ элементы в первой строке матрицы ${(G^{T} G + λ I_{h c})}^{- 1} G^{T}$ , применение отступающего принципа горизонта дает к уравнению алгоритма управления как

$D (z^{- 1}) u (k) = \sum_{j = h i}^{h p} γ_{j} [w (k + j | k) - {\hat{y}}_{0} (k + j | k)] .$

Использование замены ${\hat{y}}_{0} (k + j | k) = \frac{H_{j - d} (z^{- 1}) D (z^{- 1})}{C (z^{- 1})} u (k - 1) + \frac{F_{j - d} (z^{- 1})}{C (z^{- 1})} y (k)$ выражения эта форма уравнения алгоритма управления:

$C (z^{- 1}) D (z^{- 1}) u (k) = - \sum_{j = h i}^{h p} γ_{j} H_{j - d} (z^{- 1}) D (z^{- 1}) u (k - 1) - \sum_{j = h i}^{h p} γ_{j} F_{j - d} (z^{- 1}) y (k) + \sum_{j = h i}^{h p} γ_{j} C (z^{- 1}) w (k + j) .$

Полиномиальная форма алгоритма управления следует как

$R (z^{- 1}) u (k) + S (z^{- 1}) y (k) = T (z^{- 1}) w (k + h p),$

где:

$R (z^{- 1}) = (C (z^{- 1}) + \sum_{j = h i}^{h p} γ_{j} z^{- 1} H_{j - d} (z^{- 1})) D (z^{- 1}),$

$S (z^{- 1}) = \sum_{j = h i}^{h p} γ_{j} F_{j - d} (z^{- 1}),$

$T (z^{- 1}) = C (z^{- 1}) \sum_{j = h i}^{h p} γ_{j} z^{- h p + j} .$

Ограничения

Чтобы получить R, R и полиномы T, используют дискретное время вместо передаточной функции непрерывного времени.

Порты

Входной параметр

развернуть все

`r` — Ссылка объекта
скаляр

Системный опорный сигнал объекта.

Типы данных: single | double

`y` — Plant выход
скаляр

Системный выходной сигнал объекта.

Типы данных: single | double

Вывод

развернуть все

`u` — Контроллер выход
скаляр

Выходной сигнал системы управления.

Типы данных: single | double

Параметры

развернуть все

`Controller parameterization` — Метод параметризации
`Controller polynomials` (значение по умолчанию) | `Generate polynomials`

Метод для параметризации контроллера. Если вы знаете дискретное время R, S и значения полинома T, выбирают Controller polynomials. В противном случае выберите Generate polynomials.

Зависимости

Выбор метода параметризации включает другие параметры.

`R polynomial` — значения полинома R
1 (значение по умолчанию) | положительный, скалярный или векторный

Вектор из полиномов R для управления RST.

Зависимости

Выбор Controller polynomials для Controller parameterization параметр включает этот параметр.

`S polynomial` — значения полинома S
1 (значение по умолчанию) | положительный, скалярный или векторный

Вектор из полиномов S для управления RST.

Зависимости

Выбор Controller polynomials для Controller parameterization параметр включает этот параметр.

`T polynomial` — значения полинома T
1 (значение по умолчанию) | положительный, скалярный или векторный

Вектор из полиномов T для управления RST.

Зависимости

Выбор Controller polynomials для Controller parameterization параметр включает этот параметр.

`Model discrete transfer function numerator` — Числитель передаточной функции
1 (значение по умолчанию) | скаляр или вектор

Числитель системы дискретизировал передаточную функцию. Определить дискретную передаточную функцию, если у вас есть лицензия на Control System Toolbox™, использование c2d функция.