Частотная характеристика

Цифровая область

freqz использует основанный на БПФ алгоритм, чтобы вычислить частотную характеристику Z-преобразования цифрового фильтра. А именно, оператор

[h,w] = freqz(b,a,p)

возвращает частотную характеристику комплекса p-точки, H (e ^{j ω}), цифрового фильтра.

$H (e^{j ω}) = \frac{b (1) + b (2) e^{- j ω} + ... + b (n + 1) e^{- j ω n}}{a (1) + a (2) e^{- j ω} + ... + a (m + 1) e^{- j ω m}}$

В его самой простой форме, freqz принимает векторы коэффициентов фильтра b и a, и целочисленный p определение числа точек, в котором можно вычислить частотную характеристику. freqz возвращает комплексную частотную характеристику в векторном h, и фактическая частота указывает в векторном w в rad/s.

freqz может принять другие параметры, такие как частота дискретизации или вектор из произвольных точек частоты. Пример ниже находок частотная характеристика с 256 точками для фильтра Чебышевский Тип 1 12-го порядка. Вызов freqz задает частоту дискретизации fs из 1 000 Гц:

[b,a] = cheby1(12,0.5,200/500);
[h,f] = freqz(b,a,256,1000);

Поскольку список параметров включает частоту дискретизации, freqz возвращает векторный f это содержит 256 точек частоты между 0 и fs/2 используемый в вычислении частотной характеристики.

Примечание

Этот тулбокс использует соглашение, что модульная частота является частотой Найквиста, заданной как половина частоты дискретизации. Параметр частоты среза для всех основных функций создания фильтра нормирован на частоту Найквиста. Для системы с частотой дискретизации на 1 000 Гц, например, 300 Гц являются 300/500 = 0.6. Чтобы преобразовать нормированную частоту в угловую частоту вокруг модульного круга, умножьтесь π. Чтобы преобразовать нормированную частоту назад в герц, умножьте наполовину демонстрационную частоту.

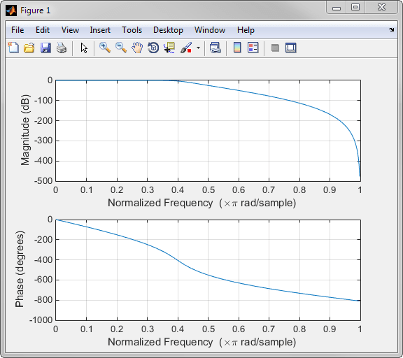
Если вы вызываете freqz без выходных аргументов это строит и величину по сравнению с частотой и фазу по сравнению с частотой. Например, девятый порядок Баттерворт фильтр lowpass с частотой среза 400 Гц, на основе частоты дискретизации на 2 000 Гц,

[b,a] = butter(9,400/1000);

Вычислить комплексную частотную характеристику с 256 точками для этого фильтра и построить величину и фазу с freqzИспользование

freqz(b,a,256,2000)

freqz может также принять вектор из произвольных точек частоты для использования в вычислении частотной характеристики. Например,

w = linspace(0,pi);
h = freqz(b,a,w);

вычисляет комплексную частотную характеристику в точках частоты в w для фильтра, заданного векторами b и a. Точки частоты могут лежать в диапазоне от 0 до 2π. Чтобы задать вектор частоты, который лежит в диапазоне от нуля до вашей частоты дискретизации, включайте и вектор частоты и значение частоты дискретизации в списке параметров.

Эти примеры показывают, как вычислить и отобразить цифровые частотные характеристики.

Частотная характеристика от передаточной функции

Скрипт Open Live Script

Вычислите и отобразите ответ величины БИХ третьего порядка фильтр lowpass, описанный следующей передаточной функцией:

$H (z) = \frac{0.05634 (1 + z^{- 1}) (1 - 1.0166 z^{- 1} + z^{- 2})}{(1 - 0.683 z^{- 1}) (1 - 1.4461 z^{- 1} + 0.7957 z^{- 2})} .$

Опишите числитель и знаменатель как полиномиальные свертки. Найдите частотную характеристику в 2 001 точке, охватывающей полный модульный круг.

b0 = 0.05634;
b1 = [1  1];
b2 = [1 -1.0166 1];
a1 = [1 -0.683];
a2 = [1 -1.4461 0.7957];

b = b0*conv(b1,b2);
a = conv(a1,a2);

[h,w] = freqz(b,a,'whole',2001);

Постройте ответ величины, описанный в децибелах.

plot(w/pi,20*log10(abs(h)))
ax = gca;
ax.YLim = [-100 20];
ax.XTick = 0:.5:2;
xlabel('Normalized Frequency (\times\pi rad/sample)')
ylabel('Magnitude (dB)')

Figure contains an axes. The axes contains an object of type line.

Частотная характеристика КИХ-полосового фильтра

Скрипт Open Live Script

Спроектируйте КИХ-полосовой фильтр с полосой пропускания между $0.35 π$ и $0.8 π$ рад/отсчет и 3 дБ пульсации. Первая полоса задерживания идет от $0$ к $0.1 π$ рад/отсчет и имеет затухание 40 дБ. Вторая полоса задерживания идет от $0.9 π$ рад/отсчет к частоте Найквиста и имеет затухание 30 дБ. Вычислите частотную характеристику. Постройте его величину и в линейных модулях и в децибелах. Подсветите полосу пропускания.

sf1 = 0.1;
pf1 = 0.35;
pf2 = 0.8;
sf2 = 0.9;
pb = linspace(pf1,pf2,1e3)*pi;

bp = designfilt('bandpassfir', ...
    'StopbandAttenuation1',40, 'StopbandFrequency1',sf1,...
    'PassbandFrequency1',pf1,'PassbandRipple',3,'PassbandFrequency2',pf2, ...
    'StopbandFrequency2',sf2,'StopbandAttenuation2',30);

[h,w] = freqz(bp,1024);
hpb = freqz(bp,pb);

subplot(2,1,1)
plot(w/pi,abs(h),pb/pi,abs(hpb),'.-')
axis([0 1 -1 2])
legend('Response','Passband','Location','South')
ylabel('Magnitude')

subplot(2,1,2)
plot(w/pi,db(h),pb/pi,db(hpb),'.-')
axis([0 1 -60 10])
xlabel('Normalized Frequency (\times\pi rad/sample)')
ylabel('Magnitude (dB)')

Figure contains 2 axes. Axes 1 contains 2 objects of type line. These objects represent Response, Passband. Axes 2 contains 2 objects of type line.

Ответ величины фильтра Highpass

Скрипт Open Live Script

Спроектируйте 3-й порядок highpass Фильтр Баттерворта, имеющий нормированную частоту на 3 дБ $0.5 π$ рад/отсчет. Вычислите его частотную характеристику. Опишите ответ величины в децибелах и постройте его.

[b,a] = butter(3,0.5,'high');
[h,w] = freqz(b,a);

dB = mag2db(abs(h));

plot(w/pi,dB)
xlabel('\omega / \pi')
ylabel('Magnitude (dB)')
ylim([-82 5])

Figure contains an axes. The axes contains an object of type line.

Повторите расчет с помощью fvtool.

fvtool(b,a)

Figure Filter Visualization Tool - Magnitude Response (dB) contains an axes and other objects of type uitoolbar, uimenu. The axes with title Magnitude Response (dB) contains an object of type line.

Аналоговая область

freqs оценивает частотную характеристику для аналогового фильтра, заданного двумя входными векторами коэффициентов, b и a. Его операция похожа на тот из freqz; можно задать много точек частоты, чтобы использовать, предоставить вектор из произвольных точек частоты и построить величину и фазовый отклик фильтра. В этом примере показано, как вычислить и отобразить аналоговые частотные характеристики.

Сравнение аналогового БИХ фильтры Lowpass

Скрипт Open Live Script

Спроектируйте аналог 5-го порядка Баттерворт фильтр lowpass с частотой среза 2 ГГц. Умножьтесь $2 π$ преобразовывать частоту в радианы в секунду. Вычислите частотную характеристику фильтра в 4 096 точках.

n = 5;
f = 2e9;

[zb,pb,kb] = butter(n,2*pi*f,'s');
[bb,ab] = zp2tf(zb,pb,kb);
[hb,wb] = freqs(bb,ab,4096);

Спроектируйте фильтр Чебышевский Тип 1 5-го порядка с той же частотой ребра и 3 дБ неравномерности в полосе пропускания. Вычислите его частотную характеристику.

[z1,p1,k1] = cheby1(n,3,2*pi*f,'s');
[b1,a1] = zp2tf(z1,p1,k1);
[h1,w1] = freqs(b1,a1,4096);

Спроектируйте 5-й порядок фильтр Типа II Чебышева с той же частотой ребра и 30 дБ затухания в полосе задерживания. Вычислите его частотную характеристику.

[z2,p2,k2] = cheby2(n,30,2*pi*f,'s');
[b2,a2] = zp2tf(z2,p2,k2);
[h2,w2] = freqs(b2,a2,4096);

Спроектируйте 5-й порядок эллиптический фильтр с той же частотой ребра, 3 дБ неравномерности в полосе пропускания и 30 дБ затухания в полосе задерживания. Вычислите его частотную характеристику.

[ze,pe,ke] = ellip(n,3,30,2*pi*f,'s');
[be,ae] = zp2tf(ze,pe,ke);
[he,we] = freqs(be,ae,4096);

Постройте затухание в децибелах. Опишите частоту в гигагерце. Сравните фильтры.

plot(wb/(2e9*pi),mag2db(abs(hb)))
hold on
plot(w1/(2e9*pi),mag2db(abs(h1)))
plot(w2/(2e9*pi),mag2db(abs(h2)))
plot(we/(2e9*pi),mag2db(abs(he)))
axis([0 4 -40 5])
grid
xlabel('Frequency (GHz)')
ylabel('Attenuation (dB)')
legend('butter','cheby1','cheby2','ellip')

Figure contains an axes. The axes contains 4 objects of type line. These objects represent butter, cheby1, cheby2, ellip.

У Баттерворта и Чебышевских фильтров Типа II есть плоские полосы пропускания и широкие полосы перехода. Чебышевский Тип I и эллиптические фильтры прокручиваются прочь быстрее, но имеют неравномерность в полосе пропускания. Вход частоты к Чебышевской функции проекта Типа II устанавливает начало полосы задерживания, а не конец полосы пропускания.

Документация