Симуляция модели динамической системы позволяет вам вникать о поведении предложенной разработки системы без трудоемкого процесса фактического создания системы. Концепции в этой теме обеспечивают контекст для понимания, как управлять симуляцией модели с программными инструментами Simulink®.
Компиляция является процессом Simulink, где block diagram переводится во внутреннее представление, которое взаимодействует с механизмом Simulink.
Нет никаких наборов уровня модели дифференциальных уравнений, которые решены численно в целом. Вместо этого уравнения уровня модели соответствуют отдельным уравнениям блока, которые решены численно в определенном порядке.
Функциональность одного блока задана несколькими уравнениями. Эти уравнения представлены как методы блока. Эти методы блока оценены (выполняемые) во время выполнения блок-схемы. Оценка этих методов блока выполняется в цикле симуляции, где каждый цикл через цикл симуляции представляет оценку блок-схемы в определенный момент времени. Общие методы блока включают:
Производная – Вычисляет производные непрерывных состояний блока на шаге текущего времени, учитывая входные параметры блока и значения состояний на предыдущем временном шаге.
Обновление – Вычисляет значение дискретных состояний блока на шаге текущего времени, учитывая его входные параметры на шаге текущего времени и его дискретные состояния на предыдущем временном шаге.
Вывод Вычисляет выходные параметры блока, учитывая его входные параметры на шаге текущего времени и его состояния на предыдущем временном шаге.

Кроме того, чтобы блокировать методы, набор методов - то, при условии, что вычисляют свойства модели и его выходные параметры. Программное обеспечение Simulink так же вызывает эти методы в процессе моделирования, чтобы определить свойства модели и ее выходные параметры. Методы модели обычно выполняют свои задачи путем вызова методов блока того же типа. Например, метод модели Outputs вызывает Выходные методы блоков, которые он содержит в порядке, заданном моделью, чтобы вычислить ее выходные параметры. Метод модели Derivatives так же вызывает методы Производных блоков, которые он содержит, чтобы определить производные его состояний.
Смотрите также: Фазы Симуляции в Динамических системах.
Коллбэки являются выражениями MATLAB, которые выполняются в ответ на определенное действие моделирования. Simulink обеспечивает параметры коллбэка модели, блока и порта, которые идентифицируют определенные виды моделирования действий. Вы предоставляете код для параметров коллбэка. Simulink выполняет код коллбэка, когда связанное действие моделирования происходит.
Параметры коллбэка модели включают:
PreloadFcn – Выполняется, прежде чем модель загружает. Например, можно предоставить код, который загружает значения переменных, которые модель использует в рабочее пространство MATLAB.
Смотрите коллбэки модели.
Блокируйтесь параметры коллбэка включают:
OpenFcn – Выполнитесь, когда вы откроете блок Subsystem.
LoadFcn – Выполнитесь после того, как схема загружается. Для Subsystem блоки также выполните параметры коллбэка блока для блоков в блоке Subsystem.
Параметр коллбэка порта:
ConnectionCallback - Выполните код каждый раз, когда возможность соединения порта изменяется.
Смотрите коллбэки порта.
Порядок выполнения является последовательностью, в котором блоке выходные методы называются после оценки прямого сквозного соединения каждого входного порта. Чтобы отобразить порядок выполнения, во вкладке Debug, выбирают Information Overlays> Execution Order.
В следующей модели блок Integrator вывел запуски сначала, и затем цикл блоков, соединенных с входом блока Integrator. Недостающие числа выполнения в последовательности обычно происходят из-за скрытых буферных блоков.
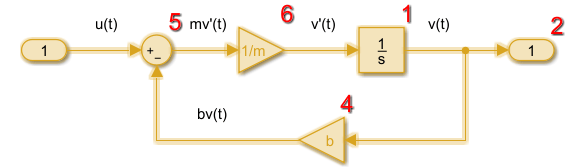
Смотрите также: Управляйте и Порядок выполнения Отображения, Фазы Симуляции в Динамических системах.
Simulation является процессом после компиляции модели, где метод блока выходные параметры и состояния вычисляется на последовательных временных шагах в области значений требуемого времени с помощью числового решателя.
Во время каждого цикла симуляции Simulink вычисляет Δt определить временной шаг t(k+1) = t(k) + Δt. Размер Δt основан на предполагаемой ошибке между симулированным решением и фактическим решением. В конце симуляции результаты данных даны как векторы [t, X, Y] в течение времени, состояния и выхода на каждом временном шаге.
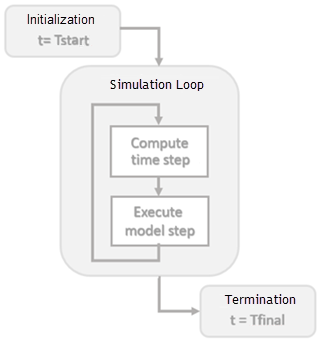
Смотрите также: Фазы Симуляции в Динамических системах, Симулируйте Модель В интерактивном режиме, Ускорьте Симуляцию.
Решатель находит приближенное решение для набора уравнений модели. Использование Simulink установило числовые решатели для этой задачи.
Размер шага решателя может быть зафиксирован или переменная:
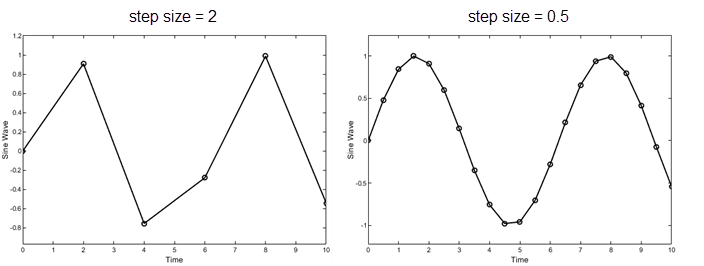
Фиксированный шаг – Временной шаг T(k+1) = T(k) + Δt где Δt является постоянным. Если размер шага является слишком большим, результаты симуляции могут иметь большую ошибку. В следующем примере, размере шага 2 искажает форму синусоидального сигнала. Можно задать размер временного шага в случае решателей фиксированного шага, или решатель может автоматически определить размер шага в случае решателей переменного шага.
Переменный шаг – Переменные решатели шага выполняют итерации, чтобы достигнуть решения на основе ошибочного допуска. Временной шаг T(k+1) = T(k) + Δtₖ где Δtₖ изменения от одного шага симуляции до следующего в зависимости от предполагаемой ошибки. Меньшие временные шаги увеличивают точность результатов симуляции. Чтобы минимизировать рабочую нагрузку расчета, решатель переменного шага выбирает самый большой размер шага, сопоставимый с достижением общего уровня точности, заданной ошибочным допуском и наблюдением нулевых пересечений. Это гарантирует, что все состояния модели вычисляются с точностью, заданной пользователем.
Выбор метода решателя зависит от природы уравнений модели. Метод Эйлера является простым числовым решателем, который вычисляет следующее значение y при помощи наклона (y') из линии касательной к y. Если y функция, которая интегрирует функцию пандуса x с наклоном 1, y' = x, и числовой решатель использовал бы следующие уравнения.
x[n+1] = x[n] + Δt*1 y[n+1] = y[n] + Δt*x[n+1]
Уменьшение размера шага увеличивает точность результатов. но это увеличивает время, чтобы завершить симуляцию. В следующем примере, размере шага 2 показывает ошибку приблизительно 20 процентов после 10 секунд в то время как размер шага 0.5 приводит к результату, который ближе к фактическому решению.