Как правило, запланированные на усиление системы управления в Simulink® используют интерполяционные таблицы или блоки MATLAB Function, чтобы задать значения усиления в зависимости от переменных планирования. Для настройки вы заменяете эти блоки параметрическими поверхностями усиления. parametric gain surface является расширением основной функции, коэффициенты которого являются настраиваемыми. Например, можно смоделировать изменяющееся во времени усиление k (t) как кубический полином в t:
k (t) = k 0 + k 1t + k 2t2 + k 3t3.
Здесь, k 0..., k 3 является настраиваемыми коэффициентами. Когда вы параметрируете запланированные усиления таким образом, systune может настроить поверхностные усилением коэффициенты, чтобы достигнуть ваших целей управления в представительном наборе условий работы. Для приложений, где усиления варьируются гладко с переменными планирования, этот подход обеспечивает явные формулы для усилений, которые программное обеспечение может записать непосредственно в блоки MATLAB Function. Когда вы используете интерполяционные таблицы, этот подход позволяет вам настроить несколько коэффициентов, а не много отдельных записей интерполяционной таблицы, решительно сокращая количество параметров и гарантируя плавные переходы между рабочими точками.
В запланированном на усиление контроллере запланированные усиления являются функциями переменных планирования, σ. Например, запланированный на усиление ПИ-контроллер имеет форму:
Настройка этого контроллера требует определения функциональных форм Kp (σ) и Ki (σ), которые дают к лучшей производительности системы в рабочем диапазоне значений σ. Однако настройка произвольных функций затрудняет. Поэтому необходимо или рассмотреть значения функции только в конечном множестве точек или ограничить общность самих функций.
В первом подходе вы выбираете набор точек проекта, σ, и настраиваете усиления Kp и Ki независимо в каждой точке проекта. Получившийся набор значений усиления хранится в интерполяционной таблице, управляемой переменными планирования, σ. Недостаток этого подхода - то, что настройка может дать к существенно различным значениям для граничения с точками проекта, вызвав нежелательные скачки при переходе от одной рабочей точки до другого.
В качестве альтернативы можно смоделировать усиления как сглаженные функции σ, но ограничить общность таких функций при помощи определенных расширений основной функции. Например, предположите, что σ является скалярной переменной. Можно смоделировать Kp (σ) как квадратичная функция σ:
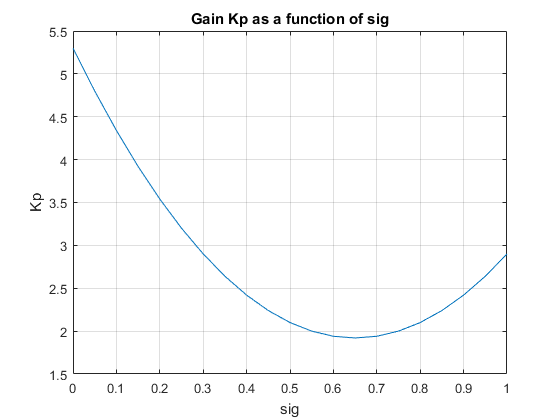
После настройки это параметрическое усиление может иметь профиль, такой как следующее (определенная форма кривой зависит от настроенных содействующих значений и области значений σ):
Или, предположите, что σ состоит из двух переменных планирования, α и V. Затем можно смоделировать Kp (σ) как билинейная функция α и V:
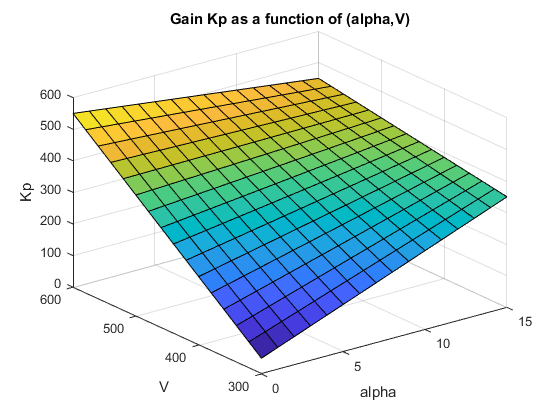
После настройки это параметрическое усиление может иметь профиль, такой как следующее. Здесь также, определенная форма кривой зависит от настроенных содействующих значений и областей значений значений σ:
Для настройки усиления планирует с systune, вы используете parametric gain surface, который является конкретным расширением усиления в основных функциях σ:
Основные функции F 1..., FM выбран пользователями и зафиксирован. Эти функции работают с n (σ), где n является функцией, которая масштабирует и нормирует переменные планирования к интервалу [–1,1] (или интервал, который вы задаете). Коэффициенты расширения, K 0..., KM, являются настраиваемыми параметрами поверхности усиления. K 0..., KM может быть скаляром или с матричным знаком, в зависимости от размера ввода-вывода усиления K (σ). Выбор основной функции зависим проблемой, но в целом, попробуйте полиномиальные расширения младшего разряда сначала.
Используйте tunableSurface команда, чтобы создать настраиваемую модель поверхности усиления, произведенной по сетке точек проекта (значения σ). Например, рассмотрите усиление с билинейной зависимостью от двух переменных планирования, α и V:
Предположим, что α является углом падения, который лежит в диапазоне от 0 ° до 15 °, и V является скоростью, которая лежит в диапазоне от 300 м/с до 700 м/с. Создайте сетку точек проекта, которые порождают эти линейные оболочки столбцов. Эти точки проекта должны совпадать со значениями параметров, в которых вы производите свое варьирование или нелинейный объект. (См. Модели объекта управления для Запланированного на усиление Контроллера, Настраивающегося.)
[alpha,V] = ndgrid(0:5:15,300:100:700); domain = struct('alpha',alpha,'V',V);
Задайте основные функции для параметризации этой поверхности, α, V и αV. tunableSurface команда ожидает, что основные функции будут расположены как вектор из функций двух входных переменных. Можно использовать анонимную функцию, чтобы описать основные функции.
shapefcn = @(alpha,V)[alpha,V,alpha*V];
В качестве альтернативы используйте polyBasis, fourierBasis, или ndBasis сгенерировать основные функции стольких переменных планирования, сколько вам нужно.
Создайте настраиваемую поверхность с помощью точек проекта и основных функций.
Kp = tunableSurface('Kp',1,domain,shapefcn);Kp настраиваемая модель поверхности усиления. tunableSurface параметрирует поверхность как:
где
Поверхность описывается в терминах нормированных переменных, вместо в терминах α и V. Эта нормализация, который tunableSurface выполняет по умолчанию, улучшает создание условий оптимизации, выполняемой systune. В случае необходимости можно изменить масштабирование по умолчанию и нормализацию. (См. tunableSurface).
Второй входной параметр к tunableSurface задает начальное значение постоянного коэффициента, K 0. По умолчанию K 0 является усилением, когда все переменные планирования находятся в центре своих областей значений. tunableSurface берет размерности ввода-вывода поверхности усиления от K 0. Поэтому можно создать настраиваемые усиления со знаком массива путем обеспечения массива для того входа.
Karr = tunableSurface('Karr',ones(2),domain,shapefcn);Karr матрица 2 на 2, в которой каждая запись является билинейной функцией переменных планирования с независимыми коэффициентами.
В этом примере показано, как смоделировать скалярное усиление K с билинейной зависимостью от двух переменных планирования. Вы делаете так путем создания сетки точек проекта, представляющих независимую зависимость этих двух переменных.
Предположим, что первая переменная α является углом падения, который лежит в диапазоне от 0 до 15 градусов, и вторая переменная V является скоростью, которая лежит в диапазоне от 300 до 600 м/с. По умолчанию нормированные переменные:
Поверхность усиления моделируется как:
где настраиваемые параметры.
Создайте сетку точек проекта, (α, V), которые линейно расположены с интервалами в α и V. Эти точки проекта являются значениями переменных планирования, используемыми для настройки поверхностных усилением коэффициентов. Они должны соответствовать значениям параметров, в которых вы произвели объект.
[alpha,V] = ndgrid(0:3:15,300:50:600);
Эти массивы, alpha и V, представляйте независимое изменение двух переменных планирования, каждого через его полный спектр. Поместите их в структуру, чтобы задать точки проекта для настраиваемой поверхности.
domain = struct('alpha',alpha,'V',V);
Создайте основные функции, которые описывают билинейное расширение.
shapefcn = @(x,y) [x,y,x*y]; % or use polyBasis('canonical',1,2)В массиве, возвращенном shapefcn, основные функции:
Создайте настраиваемую поверхность усиления.
K = tunableSurface('K',1,domain,shapefcn);Можно использовать настраиваемую поверхность в качестве параметризации для блока интерполяционной таблицы или блока MATLAB function в модели Simulink. Или, используйте команды соединения моделей, чтобы включить его как настраиваемый элемент в системе управления, смоделированной в MATLAB. После того, как вы настроите коэффициенты, можно исследовать получившуюся поверхность усиления использование viewSurf команда. В данном примере вместо настройки, вручную устанавливает коэффициенты на ненулевые значения и просматривают получившееся усиление.
Ktuned = setData(K,[100,28,40,10]); viewSurf(Ktuned)

viewSurf отображает поверхность усиления в зависимости от переменных планирования, для областей значений значений, заданных domain и сохраненный в SamplingGrid свойство поверхности усиления.
В вашей модели Simulink вы моделируете расписания усиления с помощью блоков интерполяционной таблицы, блоков MATLAB Function или блоков Matrix Interpolation, как описано в Запланированных на усиление Системах управления Модели в Simulink. Чтобы настроить эти поверхности усиления, использовать tunableSurface чтобы создать усиление появляются для каждого блока. В slTuner взаимодействуйте через интерфейс к модели, определяйте каждое расписание усиления как блок настраивать, и устанавливать свою параметризацию на соответствующую поверхность усиления. Например, rct_CSTR модель включает запланированный на усиление ПИ-контроллер, Concentration controller подсистема, в который усиления Kp и Ki меняйтесь в зависимости от переменной Cr планирования.
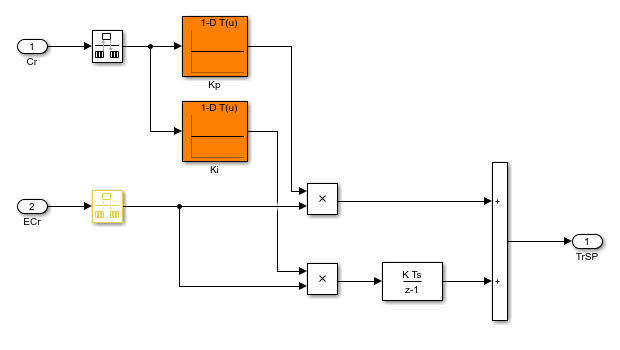
Настроить интерполяционные таблицы Kp и Ki, создайте настраиваемую поверхность для каждого. Предположим тот CrEQ вектор из точек проекта, и что вы ожидаете, что усиления будут варьироваться квадратично с Cr.
TuningGrid = struct('Cr',CrEQ); ShapeFcn = @(Cr) [Cr , Cr^2]; Kp = tunableSurface('Kp',0,TuningGrid,ShapeFcn); Ki = tunableSurface('Ki',-2,TuningGrid,ShapeFcn);
Предположим, что у вас есть массив Gd из линеаризации подсистемы объекта, CSTR, в каждом проекте указывает в CrEQ. (См. модели объекта управления для запланированного на усиление контроллера, настраивающегося). Создайте slTuner интерфейс, который заменяет этим массивом подсистему объекта и определяет два блока интерполяционной таблицы для настройки.
BlockSubs = struct('Name','rct_CSTR/CSTR','Value',Gd); ST0 = slTuner('rct_CSTR',{'Kp','Ki'},BlockSubs);
Наконец, используйте настраиваемые поверхности, чтобы параметрировать интерполяционные таблицы.
ST0.setBlockParam('Kp',Kp); ST0.setBlockParam('Ki',Ki);
Когда вы настраиваете STO, systune настраивает коэффициенты настраиваемых поверхностей Kp и Ki, так, чтобы каждая настраиваемая поверхность представляла настроенное отношение между Cr и усиление. Когда вы записываете настроенные значения обратно с блоком для валидации, setBlockParam автоматически генерирует настроенные данные интерполяционной таблицы путем оценки настраиваемых поверхностей в точках останова, которые вы задаете в соответствующих блоках.
Для получения дополнительной информации об этом примере, смотрите Запланированное на усиление Управление Химического Реактора.
Для системы управления, смоделированной в MATLAB®, используйте настраиваемые поверхности, чтобы создать более комплексные запланированные на усиление элементы управления, такие как запланированные на усиление ПИД-регуляторы, фильтры или контроллеры пространства состояний. Например, предположите, что вы создаете две поверхности усиления Kp и Ki использование tunableSurface. Следующая команда создает настраиваемый запланированный на усиление ПИ-контроллер.
C0 = pid(Kp,Ki);
Точно так же предположите, что вы создаете четыре поверхности усиления с матричным знаком ABCD. Следующая команда создает настраиваемый запланированный на усиление контроллер пространства состояний.
C1 = ss(A,B,C,D);
Вы затем включаете запланированный на усиление контроллер в обобщенную модель вашей целой системы управления. Например, предположите G массив моделей вашего объекта, произведенного в точках проекта, которые заданы в Kp и Ki. Затем следующая команда создает настраиваемую модель запланированной на усиление одноконтурной системы управления ПИДа.
T0 = feedback(G*C0,1);
Когда вы соединяете настраиваемую поверхность с другими моделями LTI, получившаяся модель является массивом обобщенных настраиваемых genss модели. Точки проекта на настраиваемой поверхности определяют размерности массива. Таким образом каждая запись в массиве представляет систему в соответствующем значении переменных планирования. SamplingGrid свойство массива хранит те точки проекта.
T0 = feedback(G*Kp,1)
T0 =
4x5 array of generalized continuous-time state-space models.
Each model has 1 outputs, 1 inputs, 3 states, and the following blocks:
Kp: Parametric 1x4 matrix, 1 occurrences.
Type "ss(T0)" to see the current value, "get(T0)" to see all properties, and
"T0.Blocks" to interact with the blocks.Получившаяся обобщенная модель имеет настраиваемые блоки, соответствующие поверхностям усиления, используемым, чтобы создать модель. В этом примере система имеет одну поверхность усиления, Kp, который имеет четыре настраиваемых коэффициента, соответствующие K 0, K 1, K 2, и K 3. Поэтому настраиваемый блок является с векторным знаком realp параметр с четырьмя записями.
Когда вы настраиваете систему управления с systune, программное обеспечение настраивает коэффициенты для каждой из точек проекта, заданных на настраиваемой поверхности.
Для примера, иллюстрирующего целый рабочий процесс в MATLAB, смотрите раздел "Controller Tuning in MATLAB" в Запланированном на усиление Управлении Химического Реактора.