Этот раздел объясняет, как Statistics and Machine Learning Toolbox™ функционирует quantile и prctile вычислите квантили и процентили.
prctile функция вычисляет процентили похожим способом как quantile вычисляет квантили. Следующие шаги в расчете квантилей также верны для процентилей, учитывая тот факт, что для той же выборки данных квантиль в значении Q совпадает с процентилью в значении P = 100*Q.
quantile первоначально присваивает отсортированные значения в X к (0.5/n), (1.5/n)..., ([n – 0.5]/n) квантили. Например:
Для вектора данных шести элементов такой как {6, 3, 2, 10, 8, 1}, отсортированные элементы {1, 2, 3, 6, 8, 10} соответственно соответствуют (0.5/6), (1.5/6), (2.5/6), (3.5/6), (4.5/6), и (5.5/6) квантили.
Для вектора данных пяти элементов такой как {2, 10, 5, 9, 13}, отсортированные элементы {2, 5, 9, 10, 13} соответственно соответствуют 0.1, 0.3, 0.5, 0.7, и 0,9 квантиля.
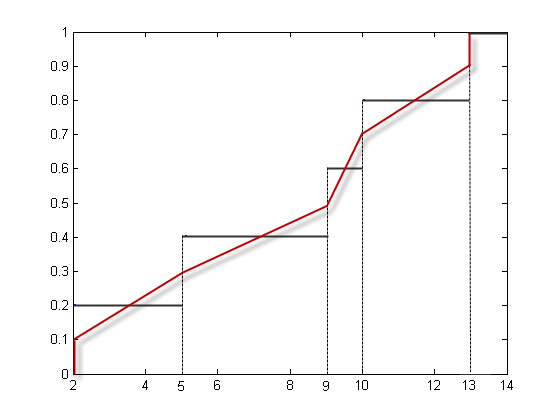
Следующая фигура иллюстрирует этот подход для вектора данных X = {2, 10, 5, 9, 13}. Первое наблюдение соответствует интегральной вероятности 1/5 = 0.2, второе наблюдение соответствует интегральной вероятности 2/5 = 0.4 и так далее. Ступенчатая функция в этом рисунке показывает эти интегральные вероятности. quantile вместо этого помещает наблюдения в средние точки, такие, что первое соответствует 0.5/5 = 0.1, второе соответствует 1.5/5 = 0.3, и так далее, и затем соединяет эти средние точки. Красные линии в следующем рисунке соединяют средние точки.
Присвоение наблюдений к квантилям
p квантили. Квантили X
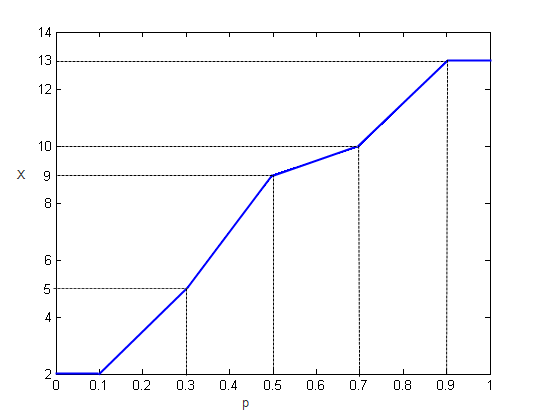
quantile находит любые квантили между значениями данных с помощью линейной интерполяции.
Линейная интерполяция использует линейные полиномы, чтобы аппроксимировать функцию f (x) и создать новые точки данных в области значений известного набора точек данных. Алгебраически, учитывая точки данных (x 1, y 1) и (x 2, y 2), где y 1 = f (x 1) и y 2 = f (x 2), линейная интерполяция находит y = f (x) для данного x между x 1 и x 2 можно следующим образом:
Точно так же, если 1.5/n квантилем является y 1.5/n, и 2.5/n квантилем является y 2.5/n, то линейная интерполяция находит 2.3/n квантиль y 2.3/n как
quantile присваивает первые и последние значения X к квантилям для вероятностей меньше, чем (0.5/n) и больше, чем ([n –0.5]/n), соответственно.
[1] Лэнгфорд, E. “Квартили в элементарной статистике”, журнал образования статистики. Издание 14, № 3, 2006.