Непрерывный вейвлет преобразовывает как полосовой фильтр

CWT как метод фильтрации

Непрерывный вейвлет преобразовывает (CWT) вычисляет скалярное произведение сигнала, $f (t)$ , с переведенными и расширенными версиями вейвлета анализа, $ψ (t) .$ Определение CWT:

$C (a, b; f (t), ψ (t)) = \int_{- \infty}^{\infty} f (t) \frac{1}{a} ψ^{*} (\frac{t - b}{a}) d t$

Можно также интерпретировать CWT как основанную на частоте фильтрацию сигнала путем перезаписи CWT как обратного преобразования Фурье.

$C (a, b; f (t), ψ (t)) = \frac{1}{2 π} \int_{- \infty}^{\infty} \hat{f} (ω) \bar{\hat{ψ}} (a ω) e^{i ω b} d ω$

где $\hat{f} (ω)$ и $\hat{ψ} (ω)$ преобразования Фурье сигнала и вейвлета.

От предыдущих уравнений вы видите, что протяжение вейвлета во время заставляет свою поддержку в частотном диапазоне уменьшаться. В дополнение к уменьшению поддержки частоты центральная частота вейвлета переключает к более низким частотам. Следующая фигура демонстрирует этот эффект для гипотетического вейвлета и шкалы (расширение) факторы 1,2, и 4.

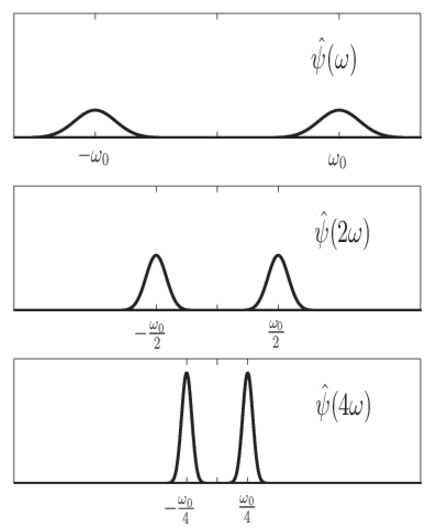
Это изображает CWT как полосовую фильтрацию входного сигнала. Коэффициенты CWT в более низких шкалах представляют энергию во входном сигнале на более высоких частотах, в то время как коэффициенты CWT в более высоких шкалах представляют энергию во входном сигнале на более низких частотах. Однако различающаяся полосовая фильтрация Фурье, ширина полосового фильтра в CWT обратно пропорциональна шкале. Ширина CWT фильтрует уменьшения с увеличивающейся шкалой. Это следует из отношений неопределенности между временем и поддержкой частоты сигнала: чем более широкий поддержка сигнала вовремя, тем более узкий его поддержка в частоте. Обратное отношение также содержит.

В вейвлете преобразовывают, шкала, или операция расширения задана, чтобы сохранить энергию. Сохранить энергию при уменьшении поддержки частоты требует, чтобы пиковый энергетический уровень увеличился. Реализация cwt в Wavelet Toolbox™ использует нормализацию L1. Добротностью или фактором Q фильтра является отношение своей пиковой энергии к пропускной способности. Поскольку уменьшение или протяжение поддержки частоты вейвлета приводят к соразмерным увеличениям или уменьшениям в его пиковой энергии, вейвлеты часто упоминаются как постоянные-Q фильтры.

Основанный на ДПФ непрерывный вейвлет преобразовывает

Уравнение в предыдущем разделе задало CWT как обратное преобразование Фурье продукта преобразований Фурье.

$C (a, b; f (t), ψ (t)) = \frac{1}{2 π} \int_{- \infty}^{\infty} \overset{\land}{f} (ω) {\hat{ψ}}^{*} (a ω) e^{j ω b} d ω$

Переменная времени в обратном преобразовании Фурье является параметром перевода, b.

Это предполагает, что можно вычислить CWT с обратным преобразованием Фурье. Поскольку существуют эффективные алгоритмы для расчета дискретного преобразования Фурье и его инверсии, можно часто достигать значительных сбережений при помощи fft и ifft если это возможно.

Чтобы получить изображение CWT в области Фурье, начните с определения вейвлета, преобразуйте:

$< f (t), ψ_{a, b} (t) > = \frac{1}{a} \int_{- \infty}^{\infty} f (t) ψ^{*} (\frac{t - b}{a}) d t$

Если вы задаете:

${\tilde{ψ}}_{a} (t) = \frac{1}{a} ψ^{*} (- t / a)$

можно переписать вейвлет, преобразовывают как

$(f * {\tilde{ψ}}_{a}) (b) = \int_{- \infty}^{\infty} f (t) {\tilde{ψ}}_{a} (b - t) d t$

который явным образом описывает CWT как свертку.

Чтобы реализовать дискретизированную версию CWT, примите, что входная последовательность является длиной N вектор, x[n]. Дискретная версия предыдущей свертки:

$W_{a} [b] = \sum_{n = 0}^{N - 1} x [n] {\tilde{ψ}}_{a} [b - n]$

Чтобы получить CWT, кажется, что необходимо вычислить свертку для каждого значения параметра сдвига, b, и повторить этот процесс для каждой шкалы, a.

Однако, если эти две последовательности циркулярно расширены (periodized к длине N), можно описать круговую свертку как продукт дискретных преобразований Фурье. CWT является обратным преобразованием Фурье продукта

$W_{a} (b) = \frac{1}{N} \sqrt{\frac{2 π}{Δ t}} \sum_{k = 0}^{N - 1} \overset{\land}{X} (2 π k / N Δ t) \overset{\land}{ψ} * (a 2 π k / N Δ t) e^{j 2 π k b / N}$

где Δt является интервалом выборки (период).

При выражении CWT, когда обратное преобразование Фурье позволяет вам использовать в вычислительном отношении эффективное fft и ifft алгоритмы, чтобы уменьшать стоимость вычислительных сверток.

cwt функционируйте реализует CWT.

Документация