Системы координат позволяют отслеживать положение и ориентацию самолета или космического аппарата в пространстве. Системы координат аэрокосмической Blockset™ основаны на этих основных концепциях геодезии, астрономии и физики.
В блоке используются правые (правые) декартовы системы координат. Правое правило устанавливает последовательность x-y-z координатных осей.
Инерционный кадр - это не ускоряющийся опорный кадр движения. В инерционном кадре второй закон Ньютона держится: сила = масса x ускорение. Нечетко говоря, ускорение определяется относительно дальнего космоса, и часто говорят, что инерционный кадр не ускоряется относительно неподвижных звезд. Поскольку Земля и звезды движутся так медленно относительно друг друга, это предположение является очень точным приближением.
Строго определяемый инерционный кадр является элементом набора всех кадров, не ускоряющихся относительно друг друга. Неинерциальный кадр - это любой кадр, ускоряющийся относительно инерционного кадра. Его ускорение, в общем, включает в себя как поступательные, так и вращательные компоненты, приводящие к псевдосилам (псевдогравитации, а также кориолисовским и центробежным силам).
Блоксет моделирует форму Земли (геоид) как сплюснутый сфероид, особый тип эллипсоида с двумя более длинными осями, равными (определяющими экваториальную плоскость) и третьей, немного более короткой (геополитической) осью симметрии. Экватор - пересечение экваториальной плоскости и поверхности Земли. Географические полюса являются пересечением земной поверхности и геополитической оси. В целом геополяры Земли и оси вращения не идентичны.
Широты параллельны экватору. Долготы параллельны геополитической оси. Нулевая долгота или простой меридиан проходит через Гринвич, Англия.
Блок делает три стандартных аппроксимации при определении систем координат относительно Земли.
Земная поверхность или геоид представляет собой сплюснутый сфероид, определяемый его более длинными экваториальными и более короткими геополитическими осями. В реальности Земля слегка деформирована по отношению к стандартному геоиду.
Ось вращения Земли и экваториальная плоскость перпендикулярны, так что оси вращения и геополитические оси идентичны. На самом деле эти оси слегка смещены, и экваториальная плоскость колеблется по мере вращения Земли. Этот эффект незначителен в большинстве применений.
Единственный неинерциальный эффект в фиксированных на Земле координатах обусловлен вращением Земли вокруг своей оси. Это вращающаяся геоцентрическая система. Блоксет игнорирует ускорение Земли вокруг Солнца, ускорение Солнца в Галактике и ускорение Галактики через космос. В большинстве применений имеет значение только вращение Земли.
Эта аппроксимация должна быть изменена для космических аппаратов, отправляемых в глубокий космос, например, вне системы Земля-Луна, и предпочтительна гелиоцентрическая система.
Блок использует стандартный геоид WGS-84 для моделирования Земли. Можно изменить длину экваториальной оси, сведение и скорость вращения.
Можно представить движение космического аппарата относительно любого небесного тела, которое хорошо аппроксимируется сплюснутым сфероидом, изменяя размер сфероида, сплющивание и скорость вращения. Если небесное тело вращается на запад (ретроградно), сделайте скорость вращения отрицательной.
Моделировать самолеты и космические аппараты проще всего, если использовать систему координат, закрепленную в самом корпусе. В случае летательных аппаратов направление движения вперед изменяется наличием ветра, и движение летательного аппарата по воздуху не совпадает с его движением относительно земли.
Дополнительные сведения о том, как блоксеть реализует координаты корпуса и ветра, см. в разделе Уравнения движения.
Неинерциальная система координат тела фиксируется как по началу, так и по ориентации к движущемуся судну. Предполагается, что судно является жестким.
Ориентация координатных осей тела фиксируется в форме тела.
Ось X указывает через нос судна.
Ось Y указывает вправо от оси X (обращенной в направлении взгляда пилота), перпендикулярно оси X.
Ось Z указывает вниз через дно судна, перпендикулярное плоскости xy и удовлетворяющее правилу RH.
Перемещения определяются перемещением по этим осям на расстояния x, y и z от начала координат.
Вращения определены угловым P Эйлера, Q, R или Φ, Θ, Ψ. Это:
| P или | Поворот вокруг оси X |
| Q или Λ | Шаг вокруг оси y |
| R или | Рыскание вокруг оси z |
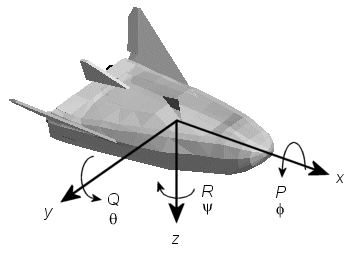
Если не указано иное, по умолчанию программа использует порядок поворота ZYX для углов Эйлера.
Неинерциальная система координат ветра имеет свое начало, зафиксированное в жестком самолете. Ориентация системы координат определяется относительно скорости V судна.
Ориентация осей координат ветра фиксируется скоростью V.
Ось X указывает в направлении V.
Ось Y указывает вправо от оси X (обращенной в направлении V), перпендикулярной оси X.
Ось Z указывает перпендикулярно плоскости xy любым способом, необходимым для выполнения правила RH относительно осей x и y.
Перемещения определяются перемещением по этим осям на расстояния x, y и z от начала координат.
Повороты определяются углами Эйлера
| Φ | Угол наклона вокруг оси X |
| γ | Траектория полета вокруг оси y |
| χ | Угол курса вокруг оси Z |
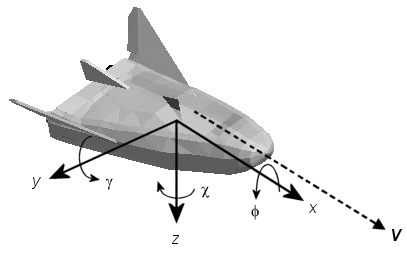
Если не указано иное, по умолчанию программа использует порядок поворота ZYX для углов Эйлера.
Моделирование аэрокосмических траекторий требует позиционирования и ориентации самолета или космического аппарата относительно вращающейся Земли. Определяют навигационные координаты относительно центра и поверхности Земли.
Геоцентрическая широта λ на поверхности Земли определяется углом, усеченным вектором радиуса от центра Земли до точки поверхности с экваториальной плоскостью.
Геодезическая широта на поверхности Земли определяется углом, усеченным вектором нормали поверхности n и экваториальной плоскостью.
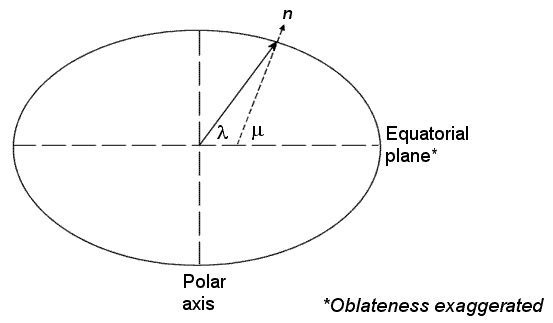
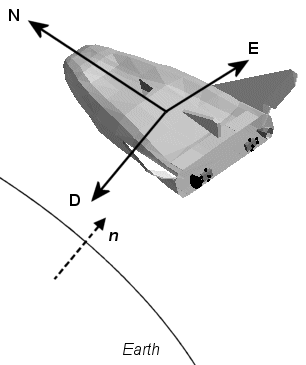
Система «север-восток-вниз» (NED) представляет собой неинерциальную систему, начало которой закреплено в центре тяжести летательного аппарата или космического аппарата. Его оси ориентированы вдоль геодезических направлений, определяемых поверхностью Земли.
Ось X указывает на север, параллельный геоидной поверхности, в полярном направлении.
Ось Y указывает на восток, параллельный поверхности геоида, вдоль кривой широты.
Ось Z указывает вниз, к поверхности Земли, антипараллельно поверхности наружу нормали n.
Полёт на постоянной высоте означает полёт на постоянной z над поверхностью Земли.
Инерционная система с центром Земли (ECI) не вращается. Для большинства применений предположим, что этот кадр является инерционным, хотя равноденствие и экваториальная плоскость с течением времени движутся очень незначительно. Система ECI считается действительно инерционной для высокоточных расчетов орбиты, когда экватор и равноденствие определяются в определенную эпоху (например, J2000). Аэрокосмические функции и блоки, использующие конкретную реализацию системы координат ECI, содержат эту информацию в своей документации. Начало координат системы ECI фиксируется в центре Земли (см. рисунок).
Ось X указывает на весеннее равноденствие (Первая точка Овна ♈).
Ось Y указывает на 90 градусов к востоку от оси X в экваториальной плоскости.
Ось Z указывает на север вдоль оси вращения Земли.
Координаты, ориентированные на Землю
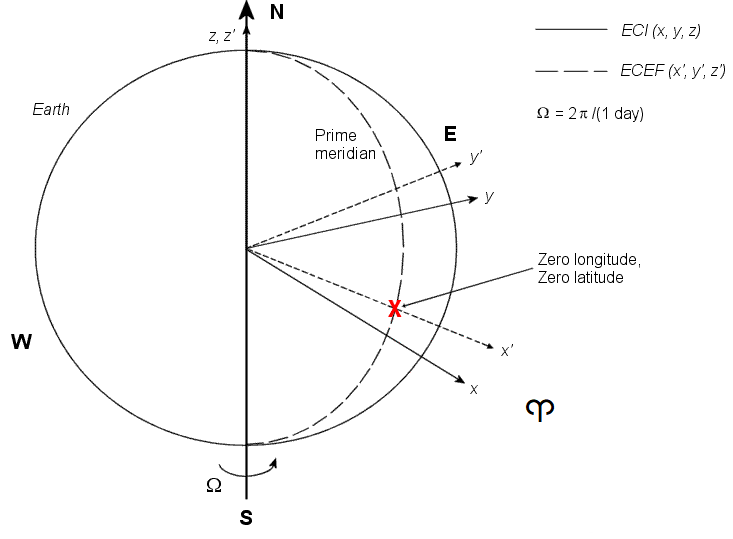
Система Земля-центр, Земля-фиксированная (ECEF) неинерционна и вращается вместе с Землей. Его начало зафиксировано в центре Земли (см. предыдущий рисунок).
Ось x ′ - указывает на пересечение экваториальной плоскости Земли и Гринвичского меридиана.
Ось y ′ - указывает на 90 градусов к востоку от оси x "- в экваториальной плоскости.
Ось Z ′ - указывает на север вдоль оси вращения Земли.
Для использования с продуктом Aerospace Blockset доступно несколько инструментов отображения. Каждая из них имеет определенную систему координат для визуализации движения.
Дополнительные сведения о координатных осях MATLAB ® Graphics см. в разделе Внешний вид осей (Axes Appearance).
MATLAB Graphics использует ориентацию оси координат по умолчанию:
Ось X указывает за пределы экрана.
Ось Y указывает вправо.
Ось Z указывает вверх.
FleyGear - симулятор полётов сторонних производителей с открытым исходным кодом с интерфейсом, поддерживаемым блоксетью.
Работа с интерфейсом симулятора полетов обсуждает интерфейс блоксети с FlireGear.
См. документацию по FleyGear по адресу www.flightgear.org для получения полной информации об этом имитаторе полета.
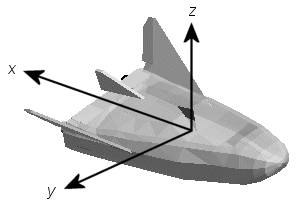
Координаты FlireGear образуют специальную систему фиксации тела, повернутую от стандартной системы координат тела вокруг оси y на -180 градусов:
Ось Х положительна к задней части транспортного средства.
Ось Y положительна справа от транспортного средства.
Ось Z положительна вверх, например, колеса обычно имеют самые низкие значения z.
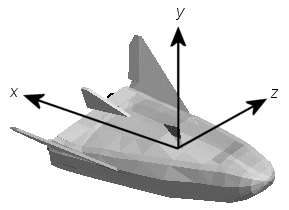
AC3D - недорогой, широко используемый редактор геометрии, доступный из https://www.inivis.com/. Его фиксированные координаты формируются инвертированием трех стандартных координатных осей тела:
Ось Х положительна к задней части транспортного средства.
Ось Y положительна вверх, например, колеса обычно имеют самые низкие значения y.
Ось Z положительна слева от транспортного средства.
[1] Рекомендуемая практика для систем координат летательных аппаратов в атмосфере и космосе, R-004-1992, ANSI/AIAA, февраль 1992 года.
[2] Роджерс, Р. М., Прикладная математика в интегрированных навигационных системах, AIAA, Рестон, Вирджиния, 2000.
[3] Собел, Д., Долгота, Уокер & Компани, Нью-Йорк, 1995.
[4] Стивенс, Б. Л., и Ф. Л. Льюис, управление и моделирование летательных аппаратов, 2-е изд., управление и моделирование летательных аппаратов, Wiley-Interscience, Нью-Йорк, 2003.
[5] Томсон, В. Т., Введение в космическую динамику, Джон Уайли и сыновья, Нью-Йорк, 1961/Dover Publications, Минеола, Нью-Йорк, 1986.