Антенна Toolbox™ использует два типа системы координат: прямоугольную систему координат и сферическую систему координат.
Панель инструментов антенны использует прямоугольную систему координат для визуализации геометрии антенны или решетки. Панель инструментов использует сферическую систему координат для визуализации диаграмм направленности антенны.
Визуализация геометрии по умолчанию monopoleTopHat антенна из антенной библиотеки.
m = monopoleTopHat; show(m);
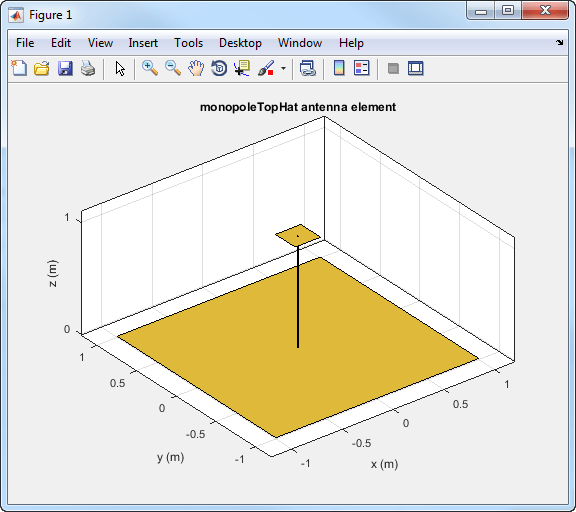
Панель инструментов отображает монопольную антенну с верхней шляпкой в прямоугольной или декартовой системе координат.
Прямоугольная система координат, также называемая декартовой системой координат, определяет положение в пространстве как упорядоченный 3-кортеж вещественных чисел, (x,y,z), в отношении происхождения (0,0,0).
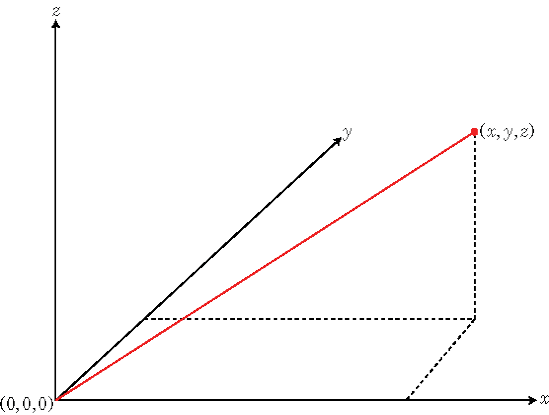
3-кортеж можно рассматривать как точку в пространстве или эквивалентно как вектор в трехмерном евклидовом пространстве. При рассмотрении в качестве вектора в пространстве координатные оси являются базисными векторами, и вектор дает направление в точку в пространстве от начала координат. Каждый вектор в пространстве однозначно определяется линейной комбинацией базисных векторов. Наиболее распространенным набором базисных векторов для трёхмерного евклидова пространства являются стандартные единичные базисные векторы:
.
Любые три линейно независимых вектора определяют основу для трехмерного пространства. Однако панель инструментов антенны предполагает, что используемые базисные векторы являются ортогональными.
Стандартной мерой расстояния в пространстве является норма l2, или евклидова норма. Евклидова норма вектора [x y z] определяется следующим образом:
Евклидова норма даёт длину вектора, измеренную от начала координат, как гипотенузу прямого треугольника. Расстояние между двумя векторами [x0 y0 z0] и [x1 y1 z1] составляет:
Визуализация диаграммы направленности по умолчанию monopoleTopHat антенна.
m = monopoleTopHat; pattern(m,75e6);
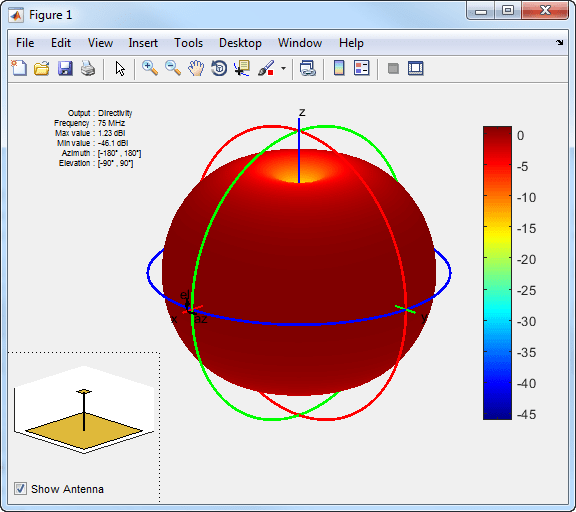
Панель инструментов отображает картину излучения верхнего шляпочного монополя с использованием сферической системы координат, представляемой углами азимута и отметки.
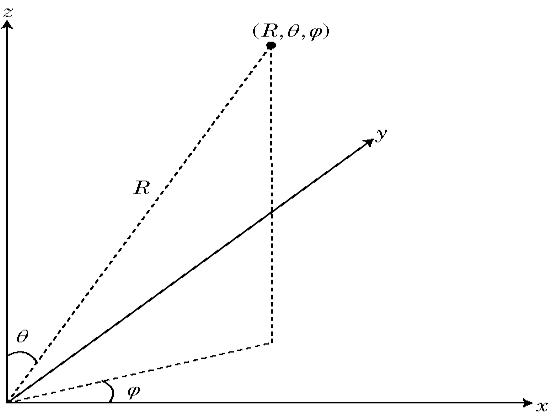
Сферическая система координат определяет вектор или точку в пространстве с расстоянием R и двумя углами. Можно представить углы в этой системе координат:
Азимут и углы места
Углы Phi (Start) и theta (start)
Координаты u и v
Азимутальный угол - это угол от положительной оси x к ортогональной проекции вектора на плоскость xy, перемещающийся в направлении к оси y. Угол азимута находится в диапазоне от -180 до 180 градусов.
Угол возвышения - это угол от ортогональной проекции вектора на плоскости xy к положительной оси z к вектору. Угол возвышения находится в диапазоне от -90 до 90 градусов.
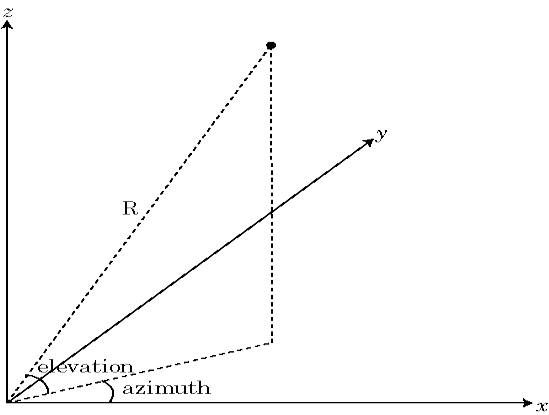
α - угол от положительной оси x к ортогональной проекции вектора на плоскость xy, движущуюся в направлении к оси y. Угол азимута находится в диапазоне от -180 до 180 градусов.
В качестве угла λ используется угол от положительной оси z до самого вектора. Этот угол находится в диапазоне от 0 до 180 градусов.
Эти углы являются альтернативой использованию азимутальных и высотных углов для выражения местоположения точки в единичной сфере.
Вы можете определить u и v в терминах
sinstart
По азимуту и углам места координаты u и v:
sinel
Значения u и v удовлетворяют неравенствам:
Углы, выраженные в u и v:
u2 + v2
Азимут и углы возвышения в пересчете на u и v составляют:
u2 − v2
Преобразуйте прямоугольные координаты в сферические (az, el, R), используя:
tan (zx2 + y2) − 1
Преобразуйте сферические координаты (az, el, R) в прямоугольные с помощью:
) z = Rsin (el)
где:
R - расстояние от антенны
el и az - азимут и углы места
[1] Баланис, С.А. Теория антенн: анализ и дизайн. 3-й эд. Нью-Йорк: Уайли, 2005.