Взаимное соединение

Взаимная связь - электромагнитное взаимодействие между антенными элементами в решетке. Ток, развиваемый в каждом антенном элементе решетки, зависит от их собственного возбуждения, а также от вклада смежных антенных элементов. Взаимная связь обратно пропорциональна расстоянию между различными антенными элементами в решетке. Взаимное соединение в массиве вызывает:

Изменение диаграммы направленности массива
Изменения входного импеданса отдельных антенных элементов в решетке

Для характеристики взаимной связи можно использовать взаимный импеданс, S-параметры, матрицу связи или шаблон встроенного элемента.

Активный импеданс или импеданс сканирования

Активный импеданс, или полное сопротивление сканирования, является входным импедансом каждого антенного элемента в решетке, когда все элементы возбуждены.

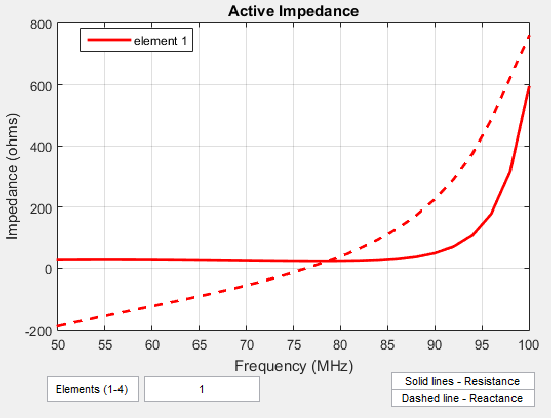
Активный импеданс матрицы зависит от:

Конфигурация массива
Интервал между элементами
Фазовый сдвиг, применяемый к каждому элементу

Взаимный импеданс

Эффект взаимной связи наблюдается или моделируется изменением пространства между антенными элементами в решетке. Любое изменение межэлементных расстояний изменяет взаимный импеданс между антенными элементами. Например, график показывает взаимный импеданс двухэлементной дипольной матрицы как функцию межэлементного интервала.

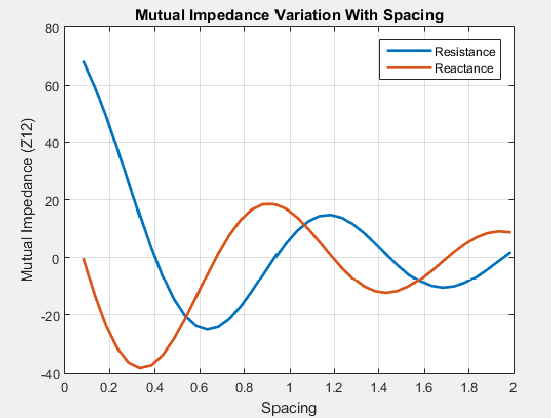
График показывает, что по мере увеличения расстояния между элементами уменьшается взаимный импеданс и, следовательно, взаимная связь.

Матрица муфты

Матрица связи используется для характеристики взаимной связи между антенными элементами на уровне порта. Эта матрица вычисляется с использованием S-параметров или Z-параметров и используется для разъединения массива.

Матрица S-параметров

Для вычисления матрицы сопряжения можно использовать матрицу S-параметров. Вы рассчитываете каждый столбец матрицы S-параметров, питая антенну в этом столбце 1V. Рассмотрим массив элементов, расположенный в сетке 2x2. Визуализация сетки и номеров элементов с помощью layout.

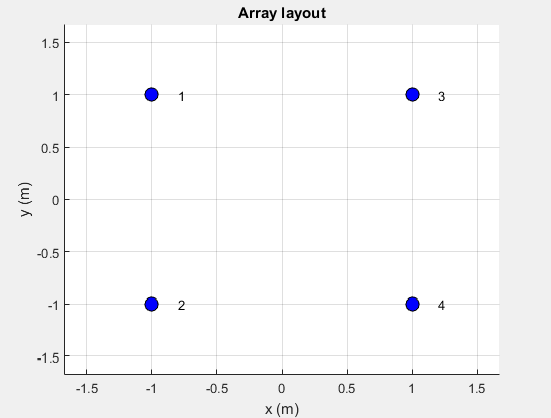
В этом массиве имеется четыре порта. Соответствующая матрица S-параметров будет иметь размер 4 x 4:

$S = \begin{matrix} _{(} & _{} & _{} & _{} \\ _{} & _{} & _{} & _{} \\ _{} & _{} & _{} & _{} \\ _{} & _{} & _{} & _{} \end{matrix}$ s11s12s13s14s21s22s23s24s31s32s33s34s41s42s43s44)

Во время этого измерения завершайте работу остальных антенных элементов, используя опорное сопротивление 50 Ом. Сопротивление окончания устанавливается по умолчанию равным 50 Ом и может быть опущено во время расчета. Если концевая заделка отличается, укажите значение сопротивления при использовании этой функции. Диагональные члены в показанной матрице представляют собой самопереключение, которое также обычно называют коэффициентом отражения. Не диагональные члены захватывают взаимную связь между портами антенны.

Использовать sparameters для вычисления матрицы связи S-параметра решетки в Toolbox™ антенны.

Коэффициент массива и умножение шаблона

Основой теории массива является теорема умножения массива. Эта теорема утверждает, что комбинированный шаблон из N идентичных элементов массива выражается как шаблон элемента, умноженный на коэффициент массива.

Коэффициент массива вычисляется по формуле:

$_{}^{} AF=∑i=0NV (i) \cdot^{ej (ksinü cosstart \cdot x (i) + ksinü sinü · y (i) +}$ kcosü· z (i))

где:

N - количество элементов в массиве.
V - приложенное напряжение (амплитуда и фаза) на каждом элементе матрицы.
k - волновое число.
тета и фи - углы возвышения и азимута.
x, y и z - декартовы координаты местоположений питания для каждого антенного элемента решетки.

Как только коэффициент решетки вычисляется с помощью вышеприведенного уравнения, можно вычислить диаграмму направленности решетки как произведение коэффициента решетки и диаграммы направленности отдельного антенного элемента решетки.

Диаграмма направленности = AF * диаграмма направленности отдельных антенных элементов

Анализ предполагает, что элементы массива разъединены. Это означает, что ток в одном элементе не возбуждает токи в других элементах или отсутствует взаимная связь между различными элементами матрицы. Это самое серьёзное ограничение теоремы умножения шаблонов, ограничивающее её использование массивами с большим интервалом элементов.

Например:

Вычислите массив прямоугольного массива диполей в плоскости x-y с интервалом в половину лямбды

fc = 1e9;
lambda = physconst('lightspeed')/fc;
az = -180:0.1:180;
el = -90:0.1:90;

%% Element
d = design(dipole,1e9);
d.Tilt = 90;
d.TiltAxis = [0 1 0];
 
%% Array
r = rectangularArray;
r.Element       = d;
r.RowSpacing    = lambda/2;
r.ColumnSpacing = lambda/2;
figure; show(r) ;
figure; patternMultiply(r, fc, az, el);

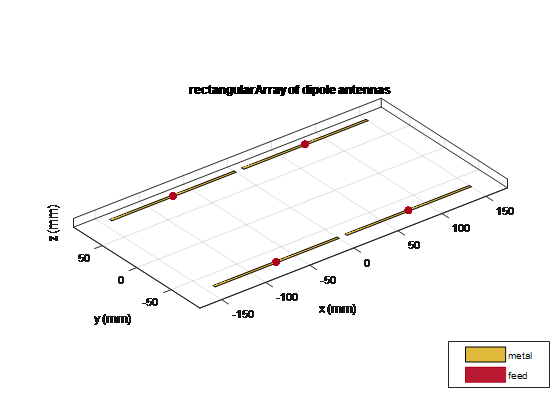
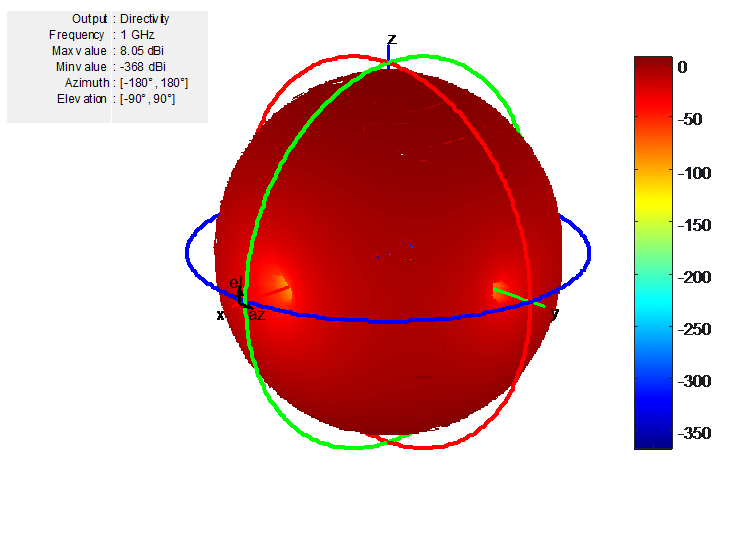
Увеличьте размер прямоугольного массива до 200 тыс. элементов. Ниже приведено время, затраченное на вычисление и вычисленную направленность.

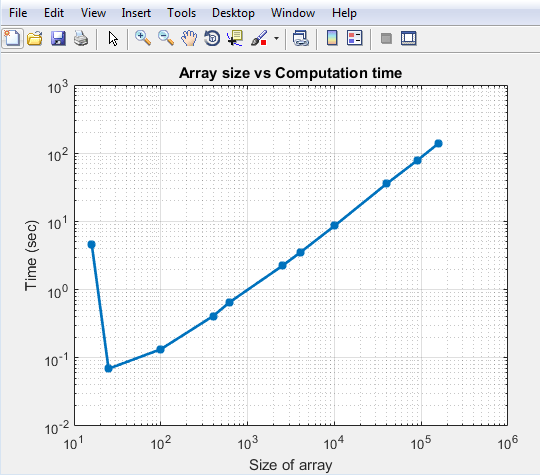
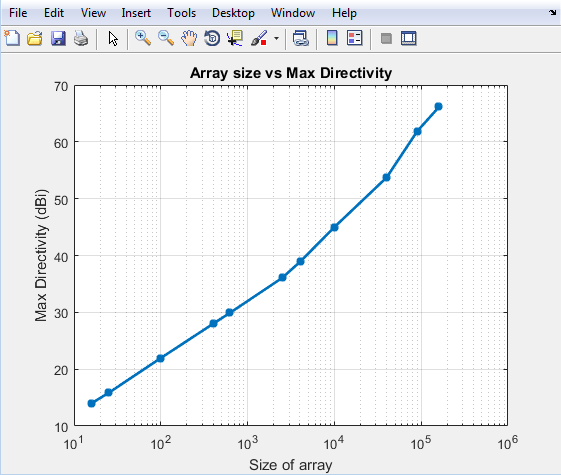
Вы видите, что время, необходимое для решения массива 100k, составляет менее 100 секунд. Начальный удар по времени для малого массива связан с тем, что выполняется анализ EM для вычисления шаблона отдельного дипольного элемента в массиве. После выполнения этого анализа результаты кэшируются, и последовательные вызовы не выполняют анализа EM. В результате увеличение времени является довольно линейным. Это самое большое преимущество использования умножения шаблонов. Она позволяет быстро решать большие массивы с ограниченными требованиями к памяти.

Образец изолированного элемента

Узоры отдельных элементов в небольших массивах значительно различаются. Поэтому нельзя использовать умножение массива для полного массива, так как шаблон изолированного элемента предполагает, что все элементы имеют один и тот же массив.

Можно рассчитать полный массив малых массивов путем печати массива всех элементов отдельно в малом массиве. Для получения этого шаблона каждый элемент возбуждается индивидуально, а остальные элементы матрицы заканчиваются с использованием опорного импеданса. На графике показана картина излучения отдельных элементов массива 4- элементов.

Образец встроенного элемента

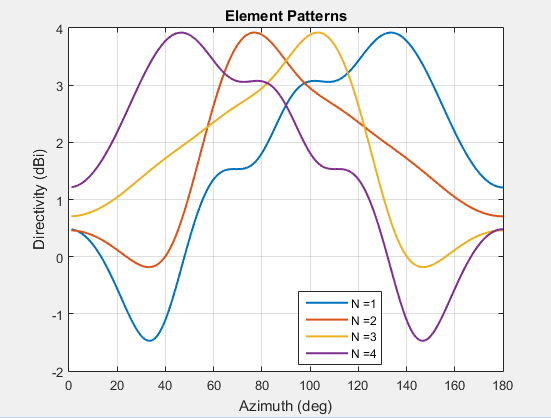
Шаблон внедренного элемента - это шаблон одного элемента, внедренного в конечный массив, рассчитанный путем управления определенным (обычно центральным) элементом в массиве. Остальные элементы матрицы заканчиваются с использованием опорного импеданса. Этот метод полезен для большого массива, поскольку эффект взаимной связи на отдельный элемент зафиксирован. Важно отметить, что граничные эффекты можно игнорировать, поскольку предполагается, что размер массива очень велик. Для этого расчета обычно используется центральный антенный элемент. Из-за размера матрицы диаграммы направленности элементов в матрице могут быть аппроксимированы шаблоном встроенных элементов вместо шаблона изолированных элементов. Наконец, для вычисления полного массива используется умножение массива.

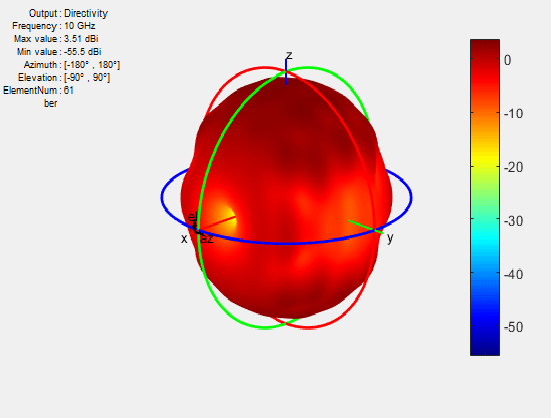
На рисунке показан образец вложенного элемента центрального элемента в 11x11 массив. Можно также вычислить образец внедренного элемента как величину электрического поля.

Шаблон изолированных элементов не рекомендуется для больших массивов, так как этот метод не учитывает эффекты соединения элементов вокруг него.

Сканирование слепоты

В больших массивах возможно резкое уменьшение направленности массива при определенных углах сканирования. При этих углах сканирования, называемых глухими углами, матрица не излучает питание, подаваемое на ее входные выводы [3]. Слепота сканирования может возникнуть при использовании этих общих механизмов:

Возбуждение поверхностных волн
Возбуждение лепестка решетки

Чтобы обнаружить слепоту сканирования в больших конечных массивах, изучите шаблон встроенного элемента. В бесконечном анализе массива этот массив известен как массив элементов массива.

Ссылки

[1] Штуцман, В. Л. Тиле, Г.А. Теория и дизайн антенн, 3-е издание. Нью-Йорк: Уайли, 2013, с. 307.

Документация