Серое кодирование - это метод, который схемы многоуровневой модуляции часто используют для минимизации частоты битовых ошибок. Он состоит из упорядочения символов модуляции таким образом, что двоичные представления соседних символов различаются только на один бит. В этом разделе показана система связи с серо-кодированной 8-арной модуляцией фазовой манипуляции (8-PSK) для сравнения характеристик частоты ошибок серого и естественного двоично-кодированного упорядочения битов.
Пример в этом разделе модулирует кадры данных с серым и натуральным двоичным кодированием с использованием метода 8-PSK. Кадры данных проходят через канал AWGN и демодулируются с использованием демодулятора 8-PSK. Вычислитель частоты ошибок Системные объекты измеряют частоту ошибок символов и битов.
В этой системе связи система модуляторов PSK возражает:
Примите двоичные входные значения, представляющие целые числа от 0 до M - 1. M - порядок модуляции и равен 8 для 8-PSK модуляции.
Отображение двоичных представлений в точки созвездия с использованием последовательности с серым и естественным двоичным кодированием.
Производить комплексные фазорные выходы единичной величины с равномерно разнесенными фазами от 0 до 2δ (M-1 )/M.
Эта таблица показывает взаимосвязь между двоичными представлениями с серым кодированием на входе и фазорами на выходе. Второй столбец таблицы является промежуточным представлением, которое объект System использует при вычислениях.
| Вход модулятора | Порядок с серым кодированием | Выход модулятора |
|---|---|---|
000 | 0 | exp(0) |
001 | 1 | exp(jδ/4) |
010 | 3 | exp(j3π/4) |
011 | 2 | exp(jδ/2) = exp(j2π/4) |
100 | 7 | exp(j7π/4) |
101 | 6 | exp(j3π/2) = exp(j6π/4) |
110 | 4 | exp(jδ) = exp(j4π/4) |
111 | 5 | exp(j5π/4) |
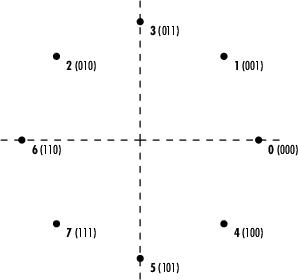
В этой таблице сортируются первые два столбца из предыдущей таблицы в соответствии с выходными значениями. Эта сортировка делает более ясным, что между соседними символами имеется только 1 битовая разница. На следующем рисунке обратите внимание, что числа во втором столбце таблицы отображаются в порядке против часовой стрелки.
| Выход модулятора | Вход модулятора |
|---|---|
exp(0) | 000 |
exp(jδ/4) | 001 |
exp(jδ/2) = exp(j2π/4) | 011 |
exp(j3π/4) | 010 |
exp(jδ) = exp(j4π/4) | 110 |
exp(j5π/4) | 111 |
exp(j3π/2) = exp(j6π/4) | 101 |
exp(j7π/4) | 100 |
Сравнение кодирования Грея с естественным двоичным кодированием с использованием соответствующим образом сконфигурированных модулятора PSK и системных объектов демодулятора PSK. Это моделирование выполняет итерацию в диапазоне от битовой энергии до спектральной плотности мощности шума, , значений и выполняется до заданного максимального количества битовых ошибок (maxNumErrs) или максимальное количество битов (maxNumBits) достигается для кодирования Грея для каждой точки Eb/N0.
Инициализация
Инициализируйте системные переменные и создайте системные объекты для операций модуляции, демодуляции, канала AWGN и частоты ошибок. С момента comm.AWGNChannel object™ системы и randi функция использует поток случайных чисел по умолчанию, задает начальное число генератора случайных чисел для обеспечения воспроизводимых результатов. Состояние генератора случайных чисел сохраняется перед установкой начального числа случайного потока и восстанавливается в конце примера.
M = 8; % Modulation order for 8-PSK
SamplesPerFrame = 10000;
maxNumErrs=100;
maxNumBits=1e8;
prevState = rng;
rng(529558);Создайте модулятор PSK, и Система демодулятора возражает, чтобы нанести на карту данные о двоичном входе к 8-PSK Серо-и закодированным набором из двух предметов созвездиям.
pskmod = comm.PSKModulator('ModulationOrder',M,'SymbolMapping','Gray', ... 'PhaseOffset',0,'BitInput',true); pskdemod = comm.PSKDemodulator('ModulationOrder',M,'SymbolMapping','Gray', ... 'PhaseOffset',0,'BitOutput',true,'OutputDataType','uint8', ... 'DecisionMethod','Hard decision'); pskmodb = comm.PSKModulator('ModulationOrder',M,'SymbolMapping','Binary', ... 'PhaseOffset',0,'BitInput',true); pskdemodb = comm.PSKDemodulator('ModulationOrder',M,'SymbolMapping','Binary', ... 'PhaseOffset',0,'BitOutput',true,'OutputDataType','uint8', ... 'DecisionMethod','Hard decision');
Создание системного объекта канала AWGN для добавления шума к модулированному сигналу. Способ шума сконфигурирован для для цикла обработки. Модулятор PSK генерирует символы с мощностью 1 Вт, поэтому свойство мощности сигнала объекта канала AWGN также устанавливается равным 1 Вт.
awgnchan = comm.AWGNChannel('NoiseMethod','Signal to noise ratio (Eb/No)', ... 'BitsPerSymbol',log2(M),'SignalPower',1);
Создайте вычислитель частоты ошибок символов и частоты ошибок битов Системные объекты для сравнения демодулированных целочисленных и битовых данных с исходными исходными данными. Это сравнение дает статистику ошибок символов и битовых ошибок. Вывод системного объекта калькулятора частоты ошибок представляет собой трехэлементный вектор, содержащий вычисленную частоту ошибок, количество обнаруженных ошибок и количество обработанных данных. Для определения времени остановки моделирования используется трехэлементный вектор.
symerror = comm.ErrorRate; biterror = comm.ErrorRate; biterrorb = comm.ErrorRate;
Цикл обработки кадров
Сконфигурируйте контур обработки кадров, в котором данные кодируются, модулируются и демодулируются с использованием 8-PSK модуляции. Контур моделирует систему связи для значений в диапазоне от 0 дБ до 12 дБ с шагом 2 дБ.
Для каждого значения Eb/N0 моделирование останавливается, если максимальное количество ошибок (maxNumErrs) или максимальное количество битов (maxNumBits), обрабатываемый вычислителем частоты битовых ошибок, достигается системный объект для битов, кодированных серым цветом.
EbNoVec = 0:2:12; % Eb/No values to simulate SERVec = zeros(size(EbNoVec)); % Initialize SER history BERVec = zeros(size(EbNoVec)); % Initialize BER history for Gray ordered BERVecb = zeros(size(EbNoVec)); % Initialize BER history for binary ordered for p = 1:length(EbNoVec) % Reset System objects reset(symerror); reset(biterror); reset(biterrorb); awgnchan.EbNo = EbNoVec(p); % Reset SER / BER for the current Eb/No value SER = zeros(3,1); BER = zeros(3,1); while (BER(2)<maxNumErrs) && (BER(3)<maxNumBits) % Generate random data txSym = randi([0 M-1],SamplesPerFrame,1,'uint8'); txBits = reshape(de2bi(txSym,log2(M),'left-msb')',[],1); % Convert symbols to bits tx = pskmod(txBits); txb = pskmodb(txBits); rx = awgnchan(tx); rxb = awgnchan(txb); rxBits = pskdemod(rx); rxBitsb = pskdemodb(rxb); rxSym = bi2de(reshape(rxBits,log2(M),[])','left-msb'); SER = symerror(txSym,rxSym); % Symbol error rate for Gray-coded data BER = biterror(txBits,rxBits); % Bit error rate for Gray-coded data BERb = biterrorb(txBits,rxBitsb); % Bit error rate for natural binary-coded data end % Save history of SER and BER values SERVec(p) = SER(1); BERVec(p) = BER(1); BERVecb(p) = BERb(1); end
Восстановите поток по умолчанию.
rng(prevState)
Анализ результатов
Проанализируйте данные из примера и сравните теоретическую производительность с производительностью моделирования. Теоретическая вероятность ошибки символа MPSK равна
(øM))
где erfc - комплементарная функция ошибки, - отношение энергии в символе к спектральной плотности мощности шума, и M - количество символов.
Чтобы определить вероятность битовой ошибки, преобразуйте вероятность символьной ошибки в ее эквивалент битовой ошибки. Нет общей формулы для преобразования символов в битовые ошибки. Тем не менее, верхний и нижний пределы легко установить. Фактическая вероятность битовых ошибок, , может быть ограничена
(M)
Нижний предел соответствует случаю, когда символы подверглись кодированию Грея. Верхний предел соответствует случаю чистого двоичного кодирования.
Рассчитайте теоретические вероятности ошибок с помощью berawgn функция. Постройте график моделируемой частоты ошибок символов для кодирования Грея, частоты битовых ошибок для кодирования Грея и естественного двоичного кодирования, а также теоретических вероятностей ошибок символов и битовых ошибок для кодирования Грея.
[theorBER,theorSER] = berawgn(EbNoVec,'psk',M,'nondiff'); figure; semilogy(EbNoVec,SERVec,'o',EbNoVec,BERVecb,'x',EbNoVec,BERVec,'*', ... EbNoVec,theorSER,'-',EbNoVec,theorBER,'-'); legend('Symbol error rate','Bit error rate (Binary)','Bit error rate (Gray)', ... 'Theoretical Symbol error rate','Theoretical Bit error rate', ... 'Location','SouthWest'); xlabel('Eb/No (dB)'); ylabel('Error Probability'); title('Symbol and Bit Error Probability'); grid on;
