Программа Toolbox™ аппроксимации кривой (Curve Fitting) позволяет рассчитать доверительные границы для подгоняемых коэффициентов и прогнозные границы для новых наблюдений или для подгоняемой функции. Кроме того, для пределов прогнозирования можно рассчитать одновременные границы, которые учитывают все предикторные значения, или можно рассчитать несимманентные границы, которые учитывают только отдельные предикторные значения. Доверительные границы коэффициентов представлены численно, в то время как прогнозируемые границы отображены графически и также доступны численно.
Доступные пределы достоверности и прогнозирования суммированы ниже.
Типы границ достоверности и прогнозирования
Тип интервала | Описание |
|---|---|
Установленные коэффициенты | Доверительные границы для соответствующих коэффициентов |
Новое наблюдение | Пределы прогнозирования для нового наблюдения (значение отклика) |
Новая функция | Пределы прогнозирования для нового значения функции |
Примечание
Границы прогнозирования также часто описываются как доверительные границы, поскольку вычисляется доверительный интервал для прогнозируемого ответа.
Пределы достоверности и прогнозирования определяют нижние и верхние значения соответствующего интервала и определяют ширину интервала. Ширина интервала указывает, насколько вы не уверены в подходящих коэффициентах, прогнозируемом наблюдении или прогнозируемом приближении. Например, очень широкий интервал для подгоняемых коэффициентов может указывать на то, что при подгонке следует использовать больше данных, прежде чем говорить что-либо очень определенное о коэффициентах.
Границы определяются с определенным уровнем достоверности. Уровень определенности часто составляет 95%, но это может быть любое значение, такое как 90%, 99%, 99,9% и так далее. Например, при прогнозировании нового наблюдения может потребоваться 5% -ная вероятность ошибки. Поэтому следует рассчитать 95% -ный интервал прогнозирования. Этот интервал указывает на 95% вероятность того, что новое наблюдение действительно содержится в пределах нижней и верхней границ прогнозирования.
Доверительные границы для установленных коэффициентов задаются
± tS
где b - коэффициенты, создаваемые аппроксимацией, t зависит от доверительного уровня и вычисляется с использованием инверсии t кумулятивной функции распределения Стьюдента, а S - вектор диагональных элементов из матрицы оцененной ковариации оценок коэффициентов, (XTX) -1s2. В линейной аппроксимации X является конструктивной матрицей, в то время как для нелинейной аппроксимации X является якобианом аппроксимированных значений относительно коэффициентов. XT - транспонирование X, а s2 - среднеквадратичная ошибка .
Доверительные границы отображаются на панели Результаты (Results) в приложении Фитинг кривой (Curve Fitting) в следующем формате.
p1 = 1.275 (1.113, 1.437)
Соответствующее значение коэффициента p1 1,275, нижняя граница 1,113, верхняя граница 1,437, ширина интервала 0,324. По умолчанию уровень достоверности для границ составляет 95%.
Можно вычислить доверительные интервалы в командной строке с помощью confint функция.
Как упоминалось выше, можно рассчитать границы прогнозирования для подогнанной кривой. Прогноз основан на существующем соответствии данным. Кроме того, границы могут быть одновременными и измерять доверие для всех значений предиктора, или они могут быть несимметричными и измерять доверие только для одного заданного значения предиктора. Если вы прогнозируете новое наблюдение, несимволические границы измеряют уверенность в том, что новое наблюдение находится в пределах интервала, заданного одним предикторным значением. Одновременные границы измеряют уверенность в том, что новое наблюдение лежит в пределах интервала независимо от значения предиктора.
| Тип привязки | Наблюдение | Функциональный |
|---|---|---|
| Одновременный |
xSxT |
fxSxT |
| Неодновременный |
xSxT |
txSxT |
Где:
s2 - среднеквадратичная ошибка
t зависит от доверительного уровня и вычисляется с использованием обратной t кумулятивной функции распределения Стьюдента
f зависит от доверительного уровня и вычисляется с использованием обратной F кумулятивной функции распределения.
S - ковариационная матрица оценок коэффициентов, (XTX) -1s2.
x - вектор строки матрицы конструкции или якобиана, вычисленный при заданном значении предиктора.
С помощью приложения «Фитинг кривой» можно графически отображать границы прогнозирования для новых наблюдений с помощью меню «Инструменты» > «Границы прогнозирования». По умолчанию уровень достоверности для границ составляет 95%. Этот уровень можно изменить на любое значение с помощью меню «Инструменты» > «Границы прогнозирования» > «Пользовательские».
Численные границы прогнозирования любого типа можно отобразить в командной строке с помощью команды predint функция.
Чтобы понять величины, связанные с каждым типом интервала прогнозирования, помните, что данные, подгонка и остатки связаны через формулу
data = аппроксимация + остатки
где члены аппроксимации и остатков являются оценками членов в формуле
data = модель + случайная ошибка
Предположим, что вы планируете сделать новое наблюдение при предикторном значении xn + 1. Вызовите новое наблюдение yn + 1 (xn + 1) и связанную с ним ошибку αn + 1. Тогда
yn + 1 (xn + 1) = f (xn + 1) + αn + 1
где f (xn + 1) - истинная, но неизвестная функция, которую нужно оценить при xn + 1. Вероятные значения для нового наблюдения или для оценочной функции обеспечиваются несимметричными границами прогнозирования.
Если вместо этого вы хотите, чтобы вероятное значение нового наблюдения было связано с любым предикторным значением, предыдущее уравнение становится
yn + 1 (x) = f (x) +
Вероятные значения для этого нового наблюдения или для оценочной функции обеспечиваются границами одновременного прогнозирования.
Типы границ прогнозирования суммированы ниже.
Типы прогнозируемых границ
Тип привязки | Одновременное или несимметричное | Связанное уравнение |
|---|---|---|
Наблюдение | Несимметричный | yn + 1 (xn + 1) |
Одновременный | yn + 1 (x), для всех x | |
Функция | Несимметричный | f (xn + 1) |
Одновременный | f (x), для всех x |
Ниже показаны несимволические и одновременные границы прогнозирования для нового наблюдения и подогнанной функции. Каждый граф содержит три кривые: подгонку, нижние доверительные границы и верхние доверительные границы. Аппроксимация является единичной экспоненциальной по отношению к сгенерированным данным, и границы отражают 95% доверительный уровень. Следует отметить, что интервалы, связанные с новым наблюдением, шире, чем соответствующие интервалы функций, из-за дополнительной неопределенности в прогнозировании нового значения отклика (кривая плюс случайные ошибки).
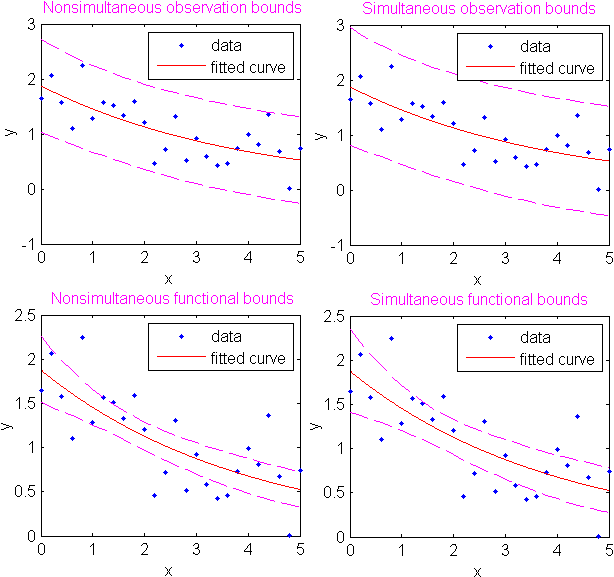
Вычислите и запишите интервалы наблюдения и функционального прогнозирования для соответствия шумным данным.
Создание шумных данных с экспоненциальным трендом.
x = (0:0.2:5)'; y = 2*exp(-0.2*x) + 0.5*randn(size(x));
Поместите кривую в данные с использованием одной экспоненциальной точки.
fitresult = fit(x,y,'exp1');Вычислите 95% интервалы наблюдения и функционального прогнозирования, как одновременные, так и несимметричные. Несимметричные границы для отдельных элементов x; одновременные границы для всех элементов x.
p11 = predint(fitresult,x,0.95,'observation','off'); p12 = predint(fitresult,x,0.95,'observation','on'); p21 = predint(fitresult,x,0.95,'functional','off'); p22 = predint(fitresult,x,0.95,'functional','on');
Постройте график интервалов данных, аппроксимации и прогнозирования. Границы наблюдения шире, чем функциональные границы, потому что они измеряют неопределенность прогнозирования подогнанной кривой плюс случайное изменение в новом наблюдении.
subplot(2,2,1) plot(fitresult,x,y), hold on, plot(x,p11,'m--'), xlim([0 5]), ylim([-1 5]) title('Nonsimultaneous Observation Bounds','FontSize',9) legend off subplot(2,2,2) plot(fitresult,x,y), hold on, plot(x,p12,'m--'), xlim([0 5]), ylim([-1 5]) title('Simultaneous Observation Bounds','FontSize',9) legend off subplot(2,2,3) plot(fitresult,x,y), hold on, plot(x,p21,'m--'), xlim([0 5]), ylim([-1 5]) title('Nonsimultaneous Functional Bounds','FontSize',9) legend off subplot(2,2,4) plot(fitresult,x,y), hold on, plot(x,p22,'m--'), xlim([0 5]), ylim([-1 5]) title('Simultaneous Functional Bounds','FontSize',9) legend({'Data','Fitted curve', 'Prediction intervals'},... 'FontSize',8,'Location','northeast')
