Остатки от подогнанной модели определяются как различия между данными ответа и соответствием данным ответа при каждом значении предиктора.
остаточный = данные - подгонка
Для отображения остатков в приложении «Фитинг кривой» выберите кнопку панели инструментов или пункт меню «Вид» > «Печать остатков».
Математически остаточное значение для конкретного значения предиктора представляет собой разность между значением y отклика и предсказанным значением ŷ отклика.
r = y - ŷ
Предполагая, что модель, вписываемая в данные, верна, остатки аппроксимируют случайные ошибки. Поэтому, если остатки, по-видимому, ведут себя случайно, это предполагает, что модель хорошо подходит для данных. Однако, если остатки отображают систематический шаблон, это явный признак того, что модель плохо подходит к данным. Всегда имейте в виду, что многие результаты подгонки модели, такие как доверительные границы, будут недействительными, если модель будет крайне неподходящей для данных.
Ниже показано графическое отображение остатков для аппроксимации полинома первой степени. Верхний график показывает, что остатки вычисляются как расстояние по вертикали от точки данных до подогнанной кривой. Нижний график отображает остатки относительно посадки, которая является нулевой линией.
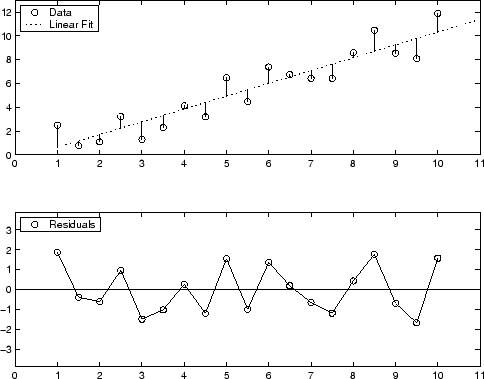
Остатки кажутся случайно разбросанными вокруг нуля, что указывает на то, что модель хорошо описывает данные.
Ниже показано графическое отображение остатков для аппроксимации полинома второй степени. Модель включает только квадратичный член и не включает линейный или постоянный член.
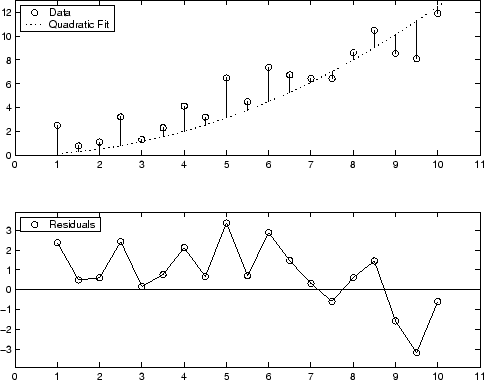
Остатки систематически являются положительными для большей части диапазона данных, указывая, что эта модель плохо подходит для данных.
Этот пример подгоняет несколько полиномиальных моделей к сформированным данным и оценивает, насколько хорошо эти модели подходят к данным и насколько точно они могут предсказать. Данные генерируются из кубической кривой, и в диапазоне переменной x имеется большой промежуток, в котором данные отсутствуют.
x = [1:0.1:3 9:0.1:10]'; c = [2.5 -0.5 1.3 -0.1]; y = c(1) + c(2)*x + c(3)*x.^2 + c(4)*x.^3 + (rand(size(x))-0.5);
Подгоните данные в приложении «Фитинг кривой» с помощью кубического многочлена и многочлена пятой степени. Данные, посадки и остатки показаны ниже. Отобразите остатки в приложении «Фитинг кривой», выбрав меню «Вид» > «Остатки» «Печать».
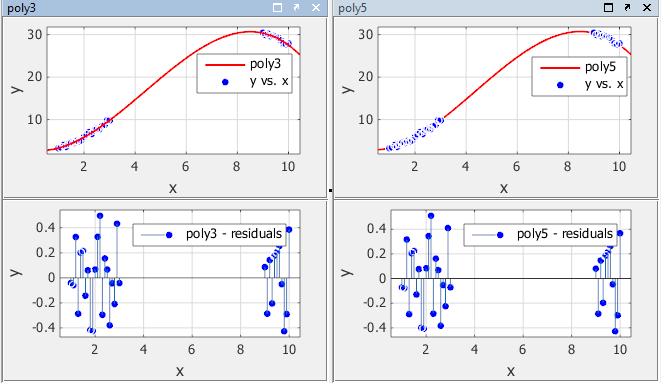
Обе модели, по-видимому, хорошо подходят к данным, и остатки, по-видимому, случайным образом распределены вокруг нуля. Поэтому графическая оценка посадок не обнаруживает никаких явных различий между двумя уравнениями.
Просмотрите результаты численного вписывания на панели Результаты (Results) и сравните доверительные границы коэффициентов.
Результаты показывают, что кубические коэффициенты подгонки точно известны (границы малы), в то время как квинтические коэффициенты подгонки точно не известны. Как и ожидалось, результаты соответствия для poly3 являются разумными, поскольку сгенерированные данные следуют кубической кривой. Доверительные границы 95% по установленным коэффициентам указывают на то, что они являются приемлемо точными. Тем не менее, 95% доверительные границы для poly5 указывают, что установленные коэффициенты точно неизвестны.
Статистические данные о пригодности приведены в таблице посадок. По умолчанию в таблице отображаются скорректированные статистические данные R-квадрата и RMSE. Статистика не показывает существенной разницы между двумя уравнениями. Чтобы выбрать статистику для отображения или скрытия, щелкните правой кнопкой мыши заголовки столбцов.
95% несимволических границ прогнозирования для новых наблюдений показаны ниже. Чтобы отобразить границы прогнозирования в приложении «Фитинг кривой», выберите «Инструменты» > «Границы прогнозирования» > 95%.
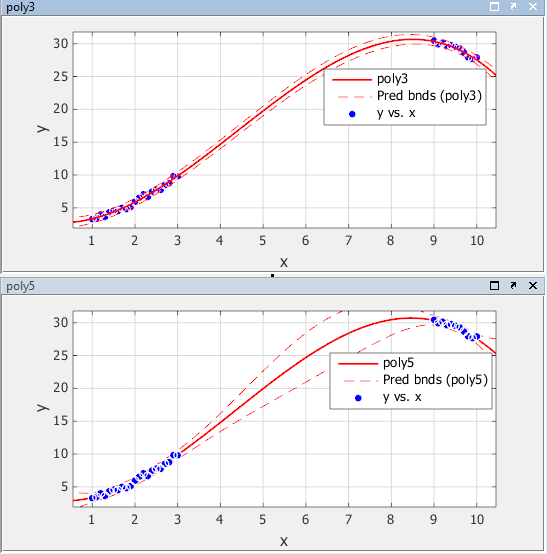
Пределы прогнозирования для poly3 указывают, что новые наблюдения могут быть предсказаны с небольшой неопределенностью во всем диапазоне данных. Это не так для poly5. Он имеет более широкие пределы прогнозирования в области, где нет данных, очевидно, потому, что данные не содержат достаточно информации для точной оценки полиномиальных членов более высокой степени. Другими словами, полином пятой степени переопределяет данные.
95% прогнозные границы для подогнанной функции с использованием poly5 показаны ниже. Как видно, неопределенность в прогнозировании функции велика в центре данных. Поэтому вы бы пришли к выводу, что необходимо собрать больше данных, прежде чем вы сможете сделать точные прогнозы с помощью полинома пятой степени.
В заключение вы должны изучить все доступные меры благости, прежде чем принимать решение о пригодности, которая лучше всего подходит для ваших целей. Графический анализ соответствия и остатков всегда должен быть вашим первоначальным подходом. Однако некоторые характеристики соответствия обнаруживаются только через численные результаты соответствия, статистику и пределы прогнозирования.