В этом разделе приведен пример создания фильтра с целочисленными коэффициентами. В этом примере создается фильтр с увеличенным косинусом с коэффициентами с плавающей запятой, а затем коэффициенты фильтра преобразуются в целые числа.
Чтобы проиллюстрировать концепции использования целых чисел с фильтрами с фиксированной точкой, в этом примере будет использован фильтр с повышенной косинусностью:
b = rcosdesign(.25, 12.5, 8, 'sqrt');
b нормализованы таким образом, что коэффициент усиления полосы пропускания равен 1 и все меньше 1. Для того, чтобы сделать их целыми числами, они должны быть масштабированы. Если вы хотите масштабировать их, чтобы использовать 18 битов для каждого коэффициента, диапазон возможных значений для коэффициентов становится следующим:
Потому что наибольший коэффициент b является положительным, его необходимо масштабировать как можно ближе к 131071 (без переполнения), чтобы минимизировать ошибку квантования. Степень масштабного коэффициента можно определить, выполнив следующие действия:
B = 18; % Number of bits L = floor(log2((2^(B-1)-1)/max(b))); % Round towards zero to avoid overflow bsc = b*2^L;
Кроме того, можно использовать инструмент автоматического масштабирования чисел с фиксированной точкой следующим образом:
bq = fi(b, true, B); % signed = true, B = 18 bits L = bq.FractionLength;
Это совпадение, что B и L оба 18 в этом случае, из-за значения наибольшего коэффициента b. Если, например, максимальное значение b были 0,124, L будет 20, пока B (количество битов) останется 18.
Сначала создайте фильтр, используя прямую форму, структуру линии задержки:
h = dfilt.dffir(bsc);
Для установки требуемых параметров арифметика должна быть установлена в фиксированную точку:
h.Arithmetic = 'fixed'; h.CoeffWordLength = 18;
Вы можете проверить, что коэффициенты h все целые числа:
all(h.Numerator == round(h.Numerator)) ans = 1
Теперь можно проверить амплитудную характеристику фильтра с помощью fvtool:
fvtool(h, 'Color', 'white')
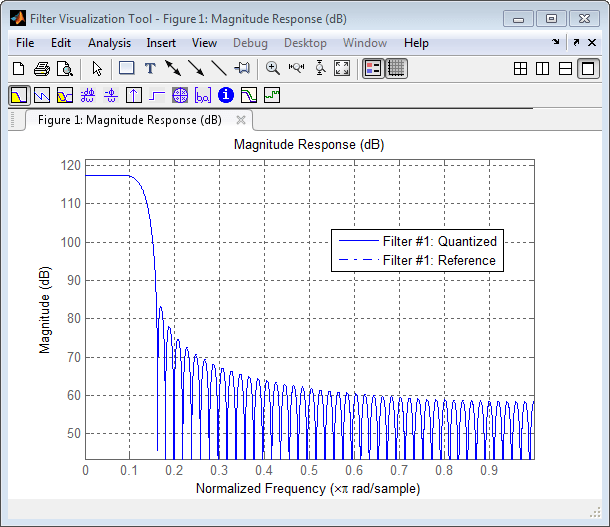
Это показывает большой коэффициент усиления 117 дБ в полосе пропускания, что обусловлено большими значениями коэффициентов - это приведет к тому, что выходной сигнал фильтра будет намного больше входного. Метод решения этой проблемы будет рассмотрен в следующих разделах.
Необходимо задать для входных параметров фильтра соответствующие значения для работы с целыми числами. Например, если вход в фильтр поступает от АЦП с 12-битовым разрешением, необходимо установить вход следующим образом:
h.InputWordLength = 12; h.InputFracLength = 0;
info возвращает сводку параметров фильтра.
info(h)
Discrete-Time FIR Filter (real) ------------------------------- Filter Structure : Direct-Form FIR Filter Length : 101 Stable : Yes Linear Phase : Yes (Type 1) Arithmetic : fixed Numerator : s18,0 -> [-131072 131072) Input : s12,0 -> [-2048 2048) Filter Internals : Full Precision Output : s31,0 -> [-1073741824 1073741824) (auto determined) Product : s29,0 -> [-268435456 268435456) (auto determined) Accumulator : s31,0 -> [-1073741824 1073741824) (auto determined) Round Mode : No rounding Overflow Mode : No overflow
В этом случае все длины дробей теперь равны нулю, что означает, что фильтр h настраивается для обработки целых чисел.
Можно создать входной сигнал для фильтра путем квантования до 12 битов с помощью функции автоматического масштабирования или выполнить ту же процедуру, которая использовалась для коэффициентов, как описано выше. В этом примере создайте сигнал с двумя синусоидами:
n = 0:999; f1 = 0.1*pi; % Normalized frequency of first sinusoid f2 = 0.8*pi; % Normalized frequency of second sinusoid x = 0.9*sin(0.1*pi*n) + 0.9*sin(0.8*pi*n); xq = fi(x, true, 12); % signed = true, B = 12 xsc = fi(xq.int, true, 12, 0);
Для фильтрации входного сигнала, сформированного выше, введите следующее:
ysc = filter(h, xsc);
Здесь ysc является выводом полной точности, означающим, что никакие биты не были отброшены в вычислениях. Это делает ysc наилучший выход, который можно получить, учитывая 12-разрядный вход и 18-разрядные коэффициенты. Это можно проверить с помощью фильтрации с двойной точностью с плавающей запятой и сравнения результатов двух операций фильтрации:
hd = double(h);
xd = double(xsc);
yd = filter(hd, xd);
norm(yd-double(ysc))
ans =
0
Теперь можно проверить выходные данные по сравнению с входными данными. В этом примере для минимизации влияния переходных процессов на график выводятся только последние несколько выборок:
idx = 800:950;
xscext = double(xsc(idx)');
gd = grpdelay(h, [f1 f2]);
yidx = idx + gd(1);
yscext = double(ysc(yidx)');
stem(n(idx)', [xscext, yscext]);
axis([800 950 -2.5e8 2.5e8]);
legend('input', 'output');
set(gcf, 'color', 'white');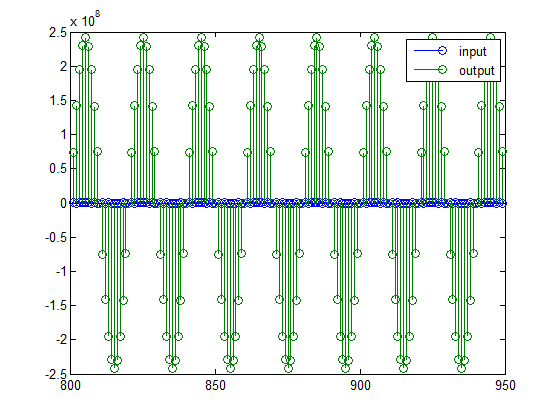
Сравнивать два сигнала на этом рисунке трудно из-за большой разницы в масштабах. Это связано с большим усилением фильтра, поэтому потребуется компенсировать усиление фильтра:
stem(n(idx)', [2^18*xscext, yscext]);
axis([800 950 -5e8 5e8]);
legend('scaled input', 'output');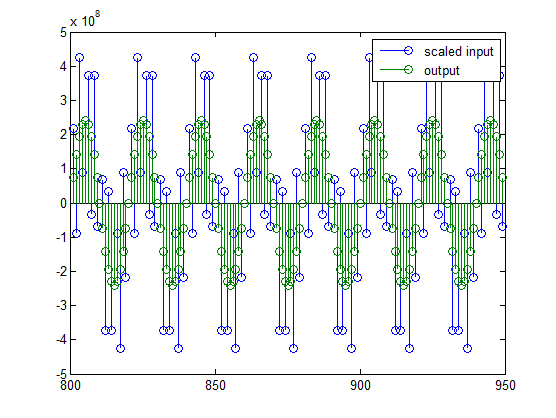
Вы можете видеть, как сигналы гораздо легче сравниваются после масштабирования, как видно на приведенном выше рисунке.
Если изучить выходную длину слова,
ysc.WordLength
ans =
31
вы заметите, что количество битов на выходе значительно больше, чем на входе. Поскольку такое увеличение числа битов, представляющих данные, может быть нежелательным, может потребоваться усечение длины слова выходного сигнала. Лучший способ сделать это - отбросить младшие биты, чтобы минимизировать ошибку. Однако, если вы знаете, что есть неиспользуемые биты высшего порядка, вы также должны отбросить эти биты.
Чтобы определить, есть ли неиспользуемые наиболее важные биты (MSB), можно посмотреть, где в вычислениях возникает рост WordLength. В этом случае увеличение битов происходит для учета результатов сложения произведений входного сигнала (12 битов) и коэффициентов (18 битов). Длина каждого из этих продуктов составляет 29 бит (проверить это можно с помощью info(h)). Рост битов, обусловленный накоплением произведения, зависит от длины фильтра и значений коэффициентов, однако это худшее определение в том смысле, что не делается никаких предположений относительно входного сигнала, и в результате могут быть неиспользуемые MSB. Тем не менее, вы должны быть осторожны, так как MSB, которые считаются неправильно использованными, вызовут переполнение.
Предположим, вы хотите сохранить 16 бит для вывода. В этом случае нет увеличения битов из-за сложений, поэтому установка выходного бита будет 16 для длины слова и -14 для длины дроби.
Поскольку фильтрация уже выполнена, можно отменить некоторые биты из ysc:
yout = fi(ysc, true, 16, -14);
Кроме того, можно задать длину выходного бита фильтра напрямую (это полезно, если планируется фильтрация многих сигналов):
specifyall(h); h.OutputWordLength = 16; h.OutputFracLength = -14; yout2 = filter(h, xsc);
Можно проверить, что результаты совпадают в любом случае:
norm(double(yout) - double(yout2))
ans =
0
Однако если сравнить это с выводом полной точности, вы заметите ошибку округления из-за отброшенных битов:
norm(double(yout)-double(ysc))
ans =
1.446323386867543e+005
В этом случае различия трудно выявить при построении графика данных, как показано ниже:
stem(n(yidx), [double(yout(yidx)'), double(ysc(yidx)')]);
axis([850 950 -2.5e8 2.5e8]);
legend('Scaled Input', 'Output');
set(gcf, 'color', 'white');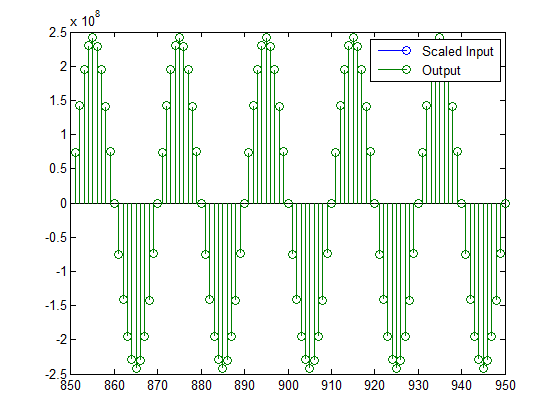
Поскольку фильтр в этом примере имеет такой большой коэффициент усиления, выходной сигнал имеет другой масштаб, чем входной сигнал. Однако это масштабирование является чисто теоретическим, и можно масштабировать данные по своему усмотрению. В этом случае у вас есть 16 бит для вывода, но вы можете присоединить любое выбранное масштабирование. Было бы естественно переосмыслить выход, чтобы иметь вес 2 ^ 0 (или L = 0) для LSB. Это эквивалентно уменьшению выходного сигнала на коэффициент 2 ^ (-14). Однако при вычислении или округлении ошибок не возникает. Для этого выполните следующие действия:
yri = fi(yout.int, true, 16, 0);
stem(n(idx)', [xscext, double(yri(yidx)')]);
axis([800 950 -1.5e4 1.5e4]);
legend('input', 'rescaled output');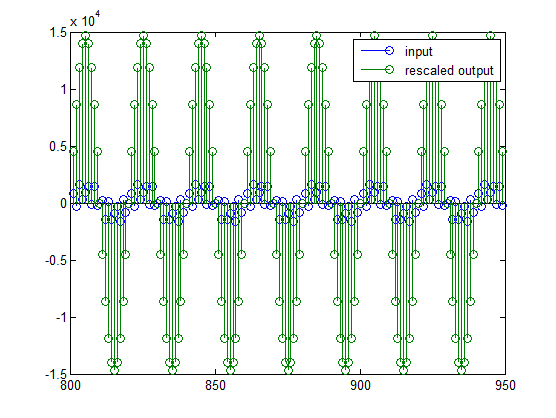
Этот график показывает, что выходной сигнал по-прежнему больше входного. Если бы вы сделали фильтрацию с двойной точностью с плавающей запятой, это было бы не так - потому что здесь для выхода используется больше битов, чем для входа, поэтому MSB взвешиваются по-разному. Вы можете увидеть этот другой способ, глядя на амплитудную характеристику масштабированного фильтра:
[H,w] = freqz(h); plot(w/pi, 20*log10(2^(-14)*abs(H)));
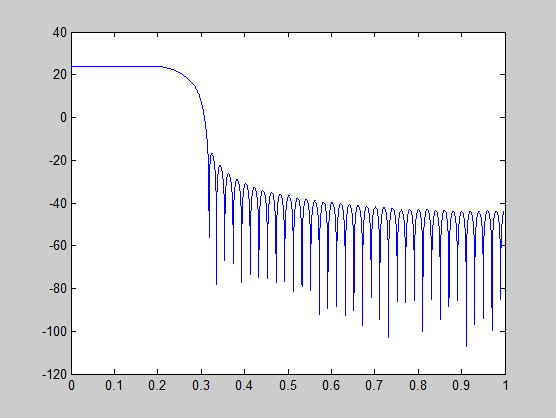
Этот график показывает, что усиление полосы пропускания все еще выше 0 дБ.
Чтобы перевести входные и выходные данные в одну шкалу, MSB должны быть взвешены одинаково. Входной MSB имеет вес 2 ^ 11, тогда как масштабированный выходной MSB имеет вес 2 ^ (29-14) = 2 ^ 15. Необходимо присвоить выходному MSB вес 2 ^ 11 следующим образом:
yf = fi(zeros(size(yri)), true, 16, 4);
yf.bin = yri.bin;
stem(n(idx)', [xscext, double(yf(yidx)')]);
legend('input', 'rescaled output');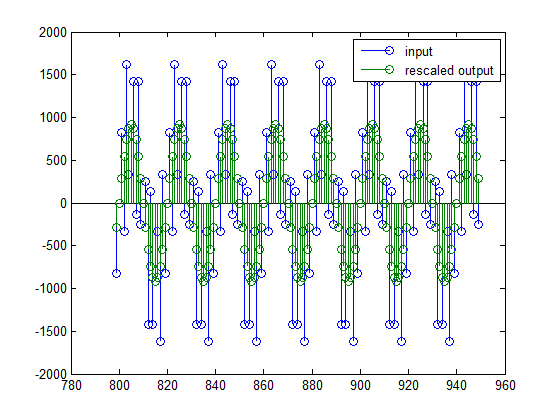
Эта операция эквивалентна уменьшению коэффициента усиления фильтра на 2 ^ (-18).
[H,w] = freqz(h); plot(w/pi, 20*log10(2^(-18)*abs(H)));
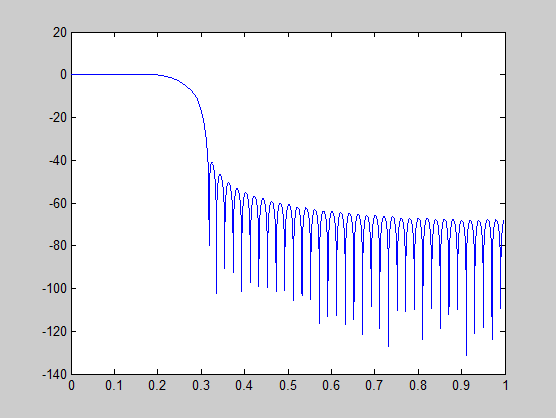
Приведенный выше график показывает коэффициент усиления 0 дБ в полосе пропускания, при необходимости.
С этой окончательной версией выходных данных, yf больше не является целым числом. Однако это связано только с интерпретацией - целые числа, представленные битами в yf идентичны тем, которые представлены битами в yri. Вы можете проверить это, сравнивая их:
max(abs(yf.int - yri.int))
ans =
0
Настройка параметров фильтра для работы с целыми числами
set2int способ обеспечивает удобный способ настройки параметров фильтра для работы с целыми числами. Метод работает путем масштабирования коэффициентов до целых чисел и установки коэффициентов и длины входной дроби на ноль. Это позволяет использовать коэффициенты с плавающей запятой непосредственно.
h = dfilt.dffir(b); h.Arithmetic = 'fixed';
Коэффициенты представлены 18 битами, а входной сигнал представлен 12 битами:
g = set2int(h, 18, 12);
g_dB = 20*log10(g)
g_dB =
1.083707984390332e+002
set2int метод возвращает коэффициент усиления фильтра путем масштабирования коэффициентов до целых чисел, поэтому коэффициент усиления всегда равен степени 2. Вы можете убедиться, что коэффициент усиления, который мы получаем здесь, соответствует коэффициенту усиления фильтра ранее. Теперь можно также проверить, что фильтр h правильно настроен для работы с целыми числами:
info(h) Discrete-Time FIR Filter (real) ------------------------------- Filter Structure : Direct-Form FIR Filter Length : 101 Stable : Yes Linear Phase : Yes (Type 1) Arithmetic : fixed Numerator : s18,0 -> [-131072 131072) Input : s12,0 -> [-2048 2048) Filter Internals : Full Precision Output : s31,0 -> [-1073741824 1073741824) (auto determined) Product : s29,0 -> [-268435456 268435456) (auto determined) Accumulator: s31,0 -> [-1073741824 1073741824) (auto determined) Round Mode : No rounding Overflow Mode : No overflow
Здесь можно увидеть, что все долевые длины теперь установлены на ноль, поэтому этот фильтр настроен правильно для работы с целыми числами.
Перетолкуйте выходные данные
Можно сравнить выходные данные с исходными данными с плавающей запятой двойной точности и проверить, что вычисления выполняются фильтром. h выполняется с полной точностью.
yint = filter(h, xsc);
norm(yd - double(yint))
ans =
0
Затем можно усечь выходной сигнал до 16 битов:
yout = fi(yint, true, 16);
stem(n(yidx), [xscext, double(yout(yidx)')]);
axis([850 950 -2.5e8 2.5e8]);
legend('input', 'output');
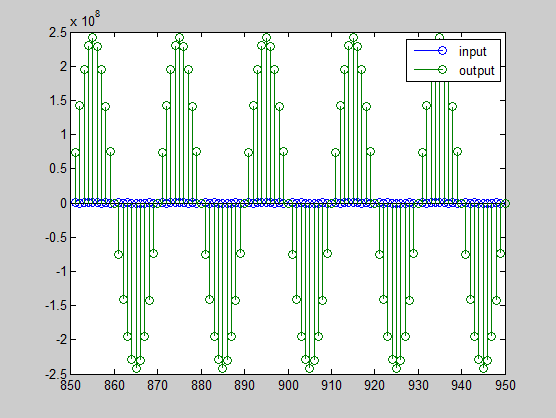
На графике также показано, что входные и выходные данные находятся в разных масштабах. Чтобы масштабировать выходной сигнал так, чтобы можно было легче сравнивать сигналы на графике, необходимо соответствующим образом взвесить MSB. Можно вычислить новую длину дроби, используя коэффициент усиления фильтра, когда коэффициенты были целыми числами:
WL = yout.WordLength;
FL = yout.FractionLength + log2(g);
yf2 = fi(zeros(size(yout)), true, WL, FL);
yf2.bin = yout.bin;
stem(n(idx)', [xscext, double(yf2(yidx)')]);
axis([800 950 -2e3 2e3]);
legend('input', 'rescaled output');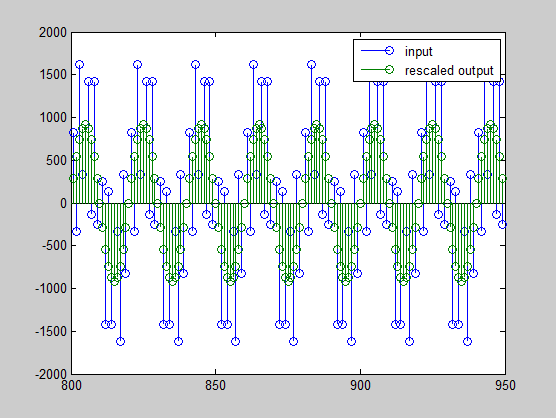
На последнем графике показаны отфильтрованные данные, повторно масштабированные в соответствии с масштабом ввода.