Фильтры FIR с фиксированной точкой обычно реализуются на процессорах цифровых сигналов, FPGA и ASIC. Фильтр с фиксированной точкой использует арифметику с фиксированной точкой и представляется уравнением с коэффициентами с фиксированной точкой. Если накопитель и выход КИХ-фильтра не имеют достаточного количества битов для представления их данных, происходит переполнение и искажает сигнал. Эти два правила используются для автоматического определения параметров точности КИХ-фильтра. Цель состоит в том, чтобы минимизировать использование ресурсов (память/память и элементы обработки), избегая переполнения. Поскольку правила оптимизированы на основе входной точности, точности коэффициентов и значений коэффициентов, фильтр FIR должен иметь неперестраиваемые коэффициенты.
Правила точности определяют минимальное и максимальное значения выходного сигнала фильтра FIR. Чтобы определить эти значения, выполните анализ min/max коэффициентов КИХ-фильтра.
Фильтр FIR определяется следующим образом:
x [n] - входной сигнал.
y [n] - выходной сигнал.
hk - коэффициент k-го фильтра.
N - длина фильтра.
Пределы выхода для фильтров FIR с реальными входными и реальными коэффициентами
Пусть минимальное значение входного сигнала - Xmin, где Xmin ≤ 0, а максимальное значение - Xmax, где Xmax ≥ 0. Минимальный выходной сигнал возникает при умножении положительных коэффициентов на Xmin и отрицательных коэффициентов на Xmax. Аналогично, максимальный выход возникает при умножении положительных коэффициентов на Xmax и отрицательных коэффициентов на Xmin.
Если сумма всех положительных коэффициентов равна
и сумма всех отрицательных коэффициентов обозначается как
затем можно выразить минимальный выходной сигнал фильтра как
G − Xmax
и максимальный выходной сигнал фильтра как
G − Xmin
Поэтому выход фильтра лежит в интервале [Ymin, Ymax].
Сложные уравнения свертки фильтра
Можно определить комплексный фильтр (комплексные входы и комплексные коэффициенты) в терминах действительной и мнимой частей его сигналов и коэффициентов:
]) +∑k=0N−1Im (hk) Re (x [n − k])
Комплексный фильтр разлагается на четыре реальных фильтра, как показано на схеме потока сигналов. Каждый сигнал аннотируется с интервалом, обозначающим его диапазон.
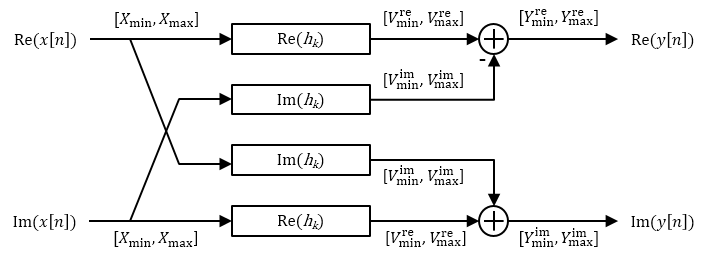
Пределы выхода для фильтров FIR с комплексными входными и комплексными коэффициентами
Анализ real filter min/max можно распространить на сложные фильтры. Предположим, что и действительная, и мнимая части входного сигнала лежат в интервале [Xmin, Xmax].
Комплексный фильтр содержит два экземпляра фильтра Re (hk). Оба фильтра имеют одинаковый диапазон ввода и, следовательно, одинаковый диапазон вывода в интервале [Vremin, Vremax]. Аналогично, комплексный фильтр содержит два экземпляра фильтра Im (hk). Оба фильтра имеют одинаковый выходной диапазон в интервале [Vimmin, Vimmax ].
На основе анализа min/max реальных фильтров можно выразить Vremin, Vremax, Vimmin и Vimmax как:
XmaxVmaxim = Gim + Xmax + Gim − Xmin
G + re - сумма положительных вещественных частей hk,
1Re (hk)
G-re - сумма отрицательных вещественных частей hk,
1Re (hk)
G + im - сумма положительных мнимых частей hk,
1Im (hk)
G-im - сумма отрицательных мнимых частей hk,
1Im (hk)
Минимальное и максимальное значения действительной и мнимой частей выходного сигнала:
Vmaxre + Vmaxim
Наихудший минимум и максимум на действительной или мнимой части выходного сигнала задается как
, Ymaxim)
Правила точности с фиксированной точкой определяют длину выходного слова и длину дроби фильтра в терминах длины слова накопителя и длины дроби.
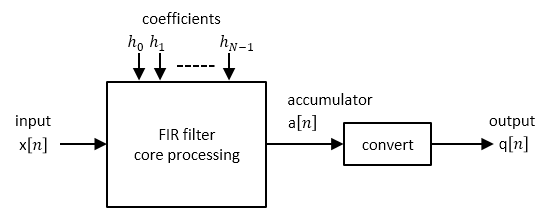
Правило накопителя полной точности
Предположим, что вход представляет собой сигнал с запятой или без знака с фиксированной точкой с длиной слова Wx и длиной дроби Fx. Также предположим, что коэффициенты являются подписанными или неподписанными значениями фиксированной точки с длиной Fh дроби. Теперь можно определить полную точность как параметры фиксированной точки, которые минимизируют длину слова накопителя, избегая переполнения или потери точности.
Длина фракции аккумулятора равна длине фракции произведения, которая является суммой длин фракции ввода и коэффициента.
+ Fh
Если Ymin = 0, то аккумулятор не подписывается длиной слова
1) ⌉
Если Ymin < 0, то накопитель подписывается длиной слова
1)) ⌉ + 1
Оператор ceil округляет до ближайшего целого числа по направлению к +∞.
Выводить ту же длину слова, что и правило ввода
Это правило устанавливает длину выходного слова равной длине входного слова. Затем он корректирует длину фракции, чтобы избежать переполнения. Wq - длина выходного слова, Fq - длина выходной дроби.
Выполните усечение накопителя, чтобы длина выходного слова совпадала с длиной входного слова.
Wx
.
Установите длину выходной фракции Fq в значение
− Wx)
.
Эти правила можно распространить на полифазные FIR-интерполяторы и прореживатели.
Интерполяторы FIR
Рассматривайте каждую полифазную ветвь FIR-интерполятора как отдельный фильтр FIR. Тип выходных данных FIR-интерполятора является наихудшим типом данных для всех многофазных ветвей.
Дециматоры FIR
Для прореживателей многофазные ветви складываются на выходе. Следовательно, тип выходных данных вычисляется, как если бы это был единственный КИХ-фильтр со всеми коэффициентами всех многофазных ветвей.