Арифметические операции

Примечание

Эти разделы помогут понять, какие типы данных и варианты масштабирования приводят к переполнению или потере точности.

Арифметика по модулю

Двоичная математика основана на арифметике по модулю. Арифметика по модулю использует только конечное множество чисел, перенося результаты любых вычислений, которые попадают за пределы данного множества обратно в множество.

Например, общие повседневные часы используют арифметику по модулю 12. Числа в этой системе могут быть только от 1 до 12. Поэтому в системе «часов» 9 плюс 9 равно 6. Это может быть легче визуализировано как круг чисел:

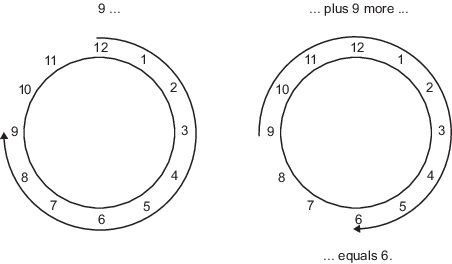
Аналогично, двоичная математика может использовать только числа 0 и 1, и любые арифметические результаты, которые выходят за пределы этого диапазона, переносятся «вокруг окружности» на 0 или 1.

Дополнение двух

Дополнение Two - это способ интерпретировать двоичное число. В дополнении двух положительные числа всегда начинаются с 0, а отрицательные - с 1. Если начальный бит числа дополнения двойки равен 0, то значение получается вычислением стандартного двоичного значения числа. Если ведущий бит числа дополнения двойки равен 1, значение получается, предполагая, что самый левый бит отрицательный, и затем вычисляя двоичное значение числа. Например,

$\begin{array}{l} ^{} \\ ^{}^{} 01=(0+20)=111=((−21)+(20))=(−2+1)=−1 \end{array}$

Чтобы вычислить негатив двоичного числа с помощью дополнения двух,

Возьмите комплемент или «переверните биты.»
Добавьте 2 ^ (-FL), используя двоичную математику, где FL - длина дроби.
Отбрасывать биты, переносимые за пределы исходной длины слова.

Например, можно принять отрицательное значение 11010 (-6). Во-первых, возьмите одно дополнение числа или переверните биты:

$11010→00101$

Затем добавьте 1, заключив все числа в 0 или 1:

$\begin{array}{l} \underset{}{\begin{array}{r} \end{array}} \\ \begin{matrix} 00101+1¯00110(6) \end{matrix} \end{array}$

Сложение и вычитание

Сложение чисел с фиксированной точкой требует выравнивания двоичных точек добавленных точек. Затем добавление выполняется с использованием двоичной арифметики, так что не используется число, отличное от 0 или 1.

Например, рассмотрим добавление 010010.1 (18.5) с 0110.110 (6.75):

$\begin{matrix} \begin{array}{r} \underset{}{\begin{matrix} \end{matrix}} \end{array} & \begin{array}{l} 010010.1+0110.110¯011001.010(18.5)(6.75)(25.25) \end{array} \end{matrix}$

Вычитание с фиксированной точкой эквивалентно добавлению при использовании значения дополнения для любых отрицательных значений. При вычитании добавленные значения должны быть расширены по знаку, чтобы соответствовать длине друг друга. Например, рассмотрим вычитание 0110.110 (6.75) из 010010.1 (18.5):

$\begin{matrix} \underset{}{\begin{matrix} \end{matrix}} & \begin{matrix} 010010.100-0110.110¯(18.5)(6.75) \end{matrix} \end{matrix}$

Fimath по умолчанию имеет значение 1 (true) для CastBeforeSum собственность. Это приводит к добавлению типа данных sum перед сложением. Поэтому дальнейшее смещение не требуется во время добавления, чтобы выстроить двоичные точки.

Если CastBeforeSum имеет значение 0 (false), добавления добавляются с сохранением полной точности. После сложения сумма затем квантуется.

Умножение

Умножение чисел двух с фиксированной точкой дополнения прямо аналогично регулярному десятичному умножению, за исключением того, что промежуточные результаты должны быть расширены так, чтобы их левые стороны выровнялись, прежде чем сложить их вместе.

Например, рассмотрим умножение 10.11 (-1.25) на 011 (3):

Типы данных умножения

На следующих диаграммах показаны типы данных, используемые для умножения с фиксированной точкой с помощью программного обеспечения Fixed-Point Designer™. Диаграммы иллюстрируют различия между типами данных, используемыми для вещественно-реального, комплексно-реального и комплексно-комплексного умножения.

Умножение в реальном масштабе. На следующей диаграмме показаны типы данных, используемые панелью инструментов при умножении двух вещественных чисел. Программа возвращает выходные данные этой операции в типе данных продукта, который управляется fimath объект ProductMode собственность.

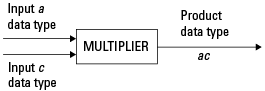
Вещественно-комплексное умножение. На следующей диаграмме показаны типы данных, используемые панелью инструментов при умножении вещественного и комплексного числа с фиксированной точкой. Вещественно-комплексное и комплексно-реальное умножение эквивалентны. Программа возвращает выходные данные этой операции в типе данных продукта, который управляется fimath объект ProductMode свойство:

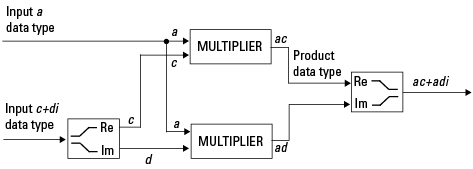
Комплексно-комплексное умножение. На следующей диаграмме показано умножение двух комплексных чисел с фиксированной точкой. Программа возвращает выходные данные этой операции в виде суммарного типа данных, который управляется fimath объект SumMode собственность. Тип данных промежуточного продукта определяется fimath объект ProductMode собственность.

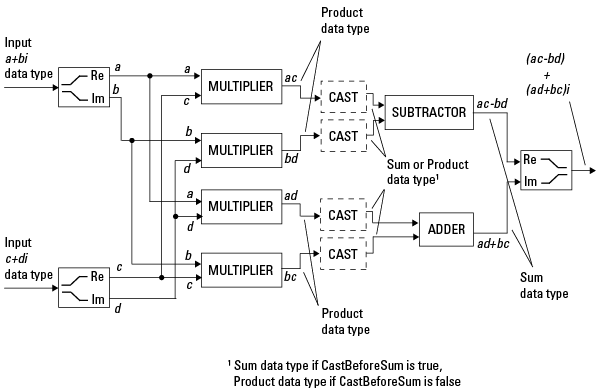
Когда fimath объект CastBeforeSum свойство - trueпосле множителей на предыдущей диаграмме присутствуют слепки на тип суммарных данных. В коде C это эквивалентно

acc=ac;
acc-=bd;

для вычитателя, и

acc=ad;
acc+=bc;

для сумматора, где acc - аккумулятор. Когда CastBeforeSum свойство - false, слепки отсутствуют, и данные остаются в типе данных продукта перед операциями вычитания и сложения.

Умножение на fimath

В следующих примерах позвольте

F = fimath('ProductMode','FullPrecision',...
'SumMode','FullPrecision');
T1 = numerictype('WordLength',24,'FractionLength',20);
T2 = numerictype('WordLength',16,'FractionLength',10);

Реал * Реал . Обратите внимание, что длина слова и длина дроби результатаz равны сумме соответственно длин слов и длин дробей умножителей. Это потому, что fimath SumMode и ProductMode свойства имеют значение FullPrecision:

P = fipref;
P.FimathDisplay = 'none';
x = fi(5,T1,F)

x = 

     5

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20

y = fi(10,T2,F)

y = 

    10

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10

z = x*y

z = 

    50

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 40
        FractionLength: 30

Комплекс Real * . Обратите внимание, что длина слова и длина дроби результатаz равны сумме соответственно длин слов и длин дробей умножителей. Это потому, что fimath SumMode и ProductMode свойства имеют значение FullPrecision:

x = fi(5,T1,F)

x = 

     5

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20

y = fi(10+2i,T2,F)

y = 

  10.0000 + 2.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10

z = x*y

z = 

  50.0000 +10.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 40
        FractionLength: 30

Комплекс * Комплекс . Комплексно-комплексное умножение включает в себя сложение, а также умножение. В результате длина слова результата полной точности имеет на один бит больше, чем сумма длин слов умножителей:

x = fi(5+6i,T1,F)

x = 

   5.0000 + 6.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20

y = fi(10+2i,T2,F)

y = 

  10.0000 + 2.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10

z = x*y

z = 

  38.0000 +70.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 41
        FractionLength: 30

Броски

fimath позволяет указать тип данных и масштабирование промежуточных сумм и продуктов с помощью SumMode и ProductMode свойства. Важно помнить о последствиях каждого литья при установке SumMode и ProductMode свойства. В зависимости от выбранных типов данных может произойти переполнение и/или округление. В следующих двух примерах показаны случаи переполнения и округления.

Примечание

Дополнительные примеры литья см. в разделе Приведение объектов fi.

Переход от более короткого типа данных к более длинному типу данных

Рассмотрим приведение ненулевого числа, представленного 4-разрядным типом данных с двумя дробными битами, к 8-разрядному типу данных с семью дробными битами:

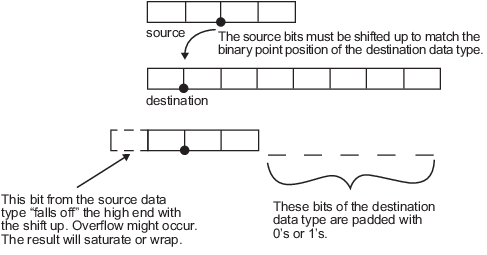
Как показано на диаграмме, исходные биты сдвигаются вверх так, чтобы двоичная точка соответствовала позиции целевой двоичной точки. Высший исходный бит не подходит, поэтому может произойти переполнение и результат может насытиться или обернуться. Пустые биты на нижнем конце типа данных назначения дополняются либо 0, либо 1:

Если переполнение не происходит, пустые биты заполняются нулями.
Если происходит сворачивание, пустые биты заполняются нулями.
Если происходит насыщение,
- Пустые биты положительного числа дополняются 1.
- Пустые биты отрицательного числа дополняются нулями.

Можно видеть, что даже в случае приведения от более короткого типа данных к более длинному типу данных по-прежнему может происходить переполнение. Это может произойти, когда целочисленная длина исходного типа данных (в данном случае два) больше, чем целочисленная длина целевого типа данных (в данном случае один). Аналогично, округление может быть необходимо даже при кадрировании из более короткого типа данных в более длинный тип данных, если целевой тип данных и масштабирование имеют меньше дробных битов, чем источник.

Переход от более длинного типа данных к более короткому типу данных

Рассмотрим приведение ненулевого числа, представленного 8-разрядным типом данных с семью дробными битами, к 4-разрядному типу данных с двумя дробными битами:

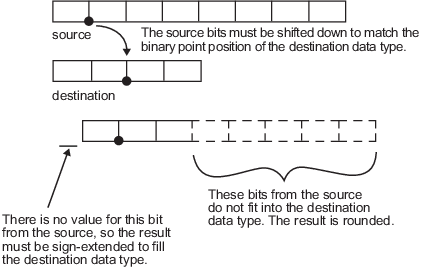
Как показано на диаграмме, исходные биты сдвигаются вниз, так что двоичная точка совпадает с позицией целевой двоичной точки. Нет значения для самого высокого бита от источника, поэтому расширение знака используется для заполнения целочисленной части целевого типа данных. Расширение знака - это добавление битов, которые имеют значение наиболее значащих битов к верхнему концу числа дополнения двух. Расширение знака не изменяет значение двоичного числа. В этом примере нижние пять битов источника не вписываются в длину дроби места назначения. Следовательно, точность может быть потеряна по мере округления результата.

В этом случае, даже если приведение происходит от более длинного типа данных к более короткому типу данных, все целочисленные биты сохраняются. И наоборот, полная точность может поддерживаться даже при приведении к более короткому типу данных, если длина дроби целевого типа данных равна или больше длины дроби исходного типа данных. В этом случае, однако, биты теряются от верхнего конца результата и может произойти переполнение.

Наихудший случай возникает, когда и целочисленная, и дробная длина целевого типа данных короче, чем у исходного типа данных и масштабирования. В этом случае может произойти как переполнение, так и потеря точности.

Документация