В общем, прямая реализация формы относится к структуре, где коэффициенты передаточной функции появляются непосредственно как блоки усиления. Способ реализации прямой формы II представлен как использующий минимальное количество элементов задержки, равное n, порядка знаменателя передаточной функции.
Каноническая прямая форма II представлена как «Стандартное программирование» в дискретных системах управления временем компанией Ogata. Она известна как «Управляющая каноническая форма» в цифровом управлении динамическими системами Франклина, Пауэлла и Уоркмана.
Можно вывести реализацию канонической прямой формы II, записав дискретно-временную передаточную функцию с входом e (z) и выходом u (z) как
11 + a1z − 1 + a2z − 2... +anz−n︸h (z) e (z).
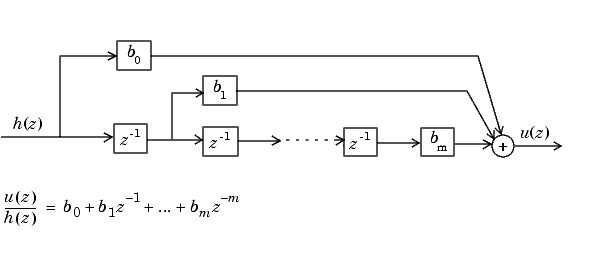
Ниже приведена блок-схема u (z )/h (z).
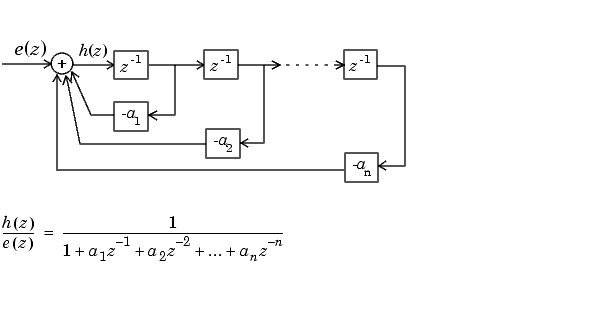
Ниже приведены блок-схемы h (z )/e (z).
Объединение этих двух блок-схем дает диаграмму прямой формы II, показанную на следующем рисунке. Обратите внимание, что часть прямой связи (верхняя часть блок-схемы) содержит коэффициенты числителя, а часть обратной связи (нижняя часть блок-схемы) содержит коэффициенты знаменателя.
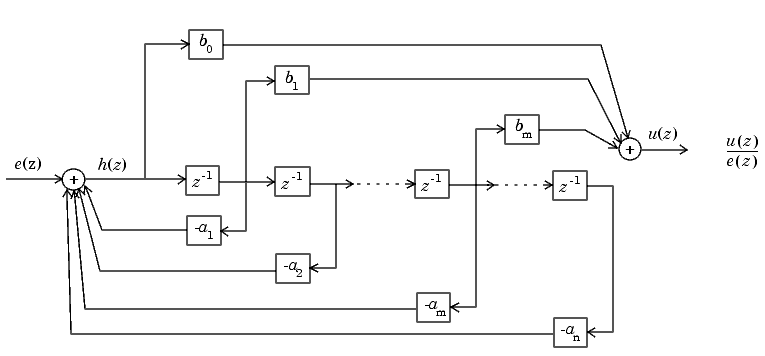
Прямая форма II пример передаточной функции дается
5z − 1 + 0 .84z − 2 + 0 .09z − 3.
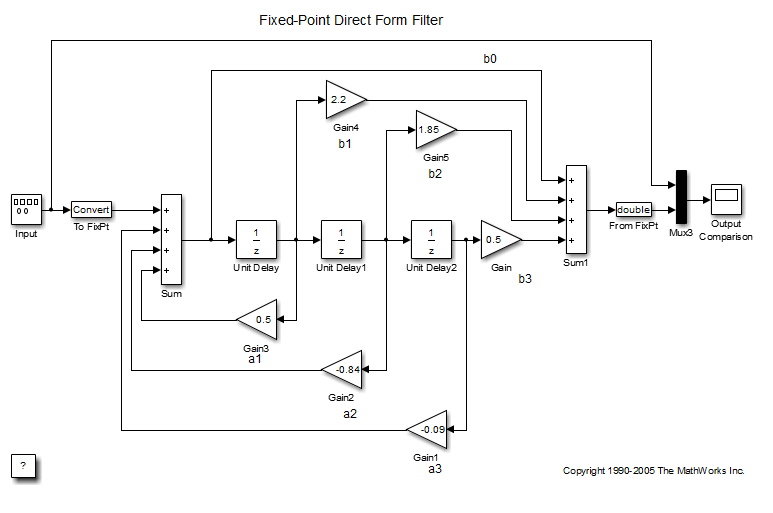
Реализация Hex (z) с использованием блоков Simulink ® с фиксированной точкой показана на следующем рисунке. Можно отобразить эту модель, введя
fxpdemo_direct_form2
в командной строке MATLAB ®.