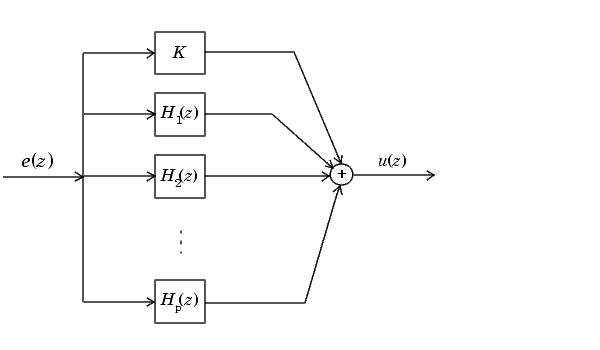
В канонической параллельной форме передаточная функция H (z) расширяется на частичные дроби. Затем H (z) реализуется как сумма функций переноса константы, первого порядка и второго порядка, как показано:
H2 (z) +... + Hp (z).
Это расширение, где K - константа, а Hi (z) - передаточные функции первого и второго порядка, следует далее.
Как и в канонической форме серии, отсутствует уникальное описание функции переноса первого и второго порядка. Из-за характера блока Sum порядок отдельных фильтров не имеет значения. Однако из-за константы K можно выбрать функции переноса первого и второго порядка так, чтобы их формы были проще, чем для каскадной формы серии, описанной в предыдущем разделе. Это делается путем расширения H (z) в виде
ciz − 1 + diz − 2.
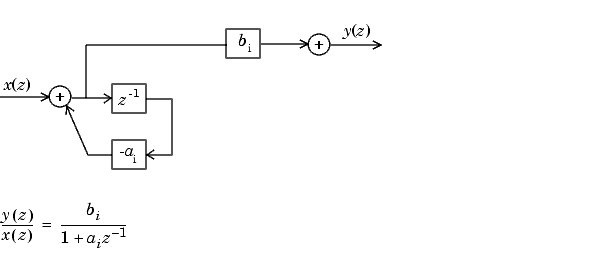
Ниже приведена диаграмма первого порядка для H (z).
Ниже приведена диаграмма второго порядка для H (z).
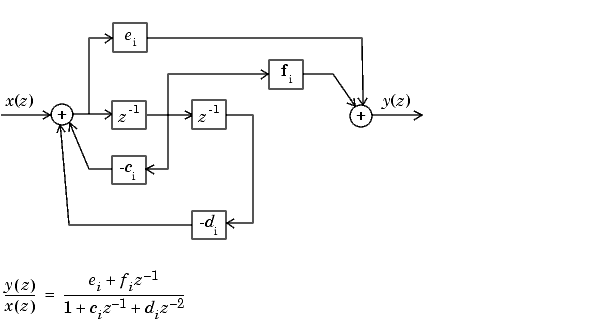
Функция передачи примера параллельной формы задается
11 − 0 .6z − 1 + 0 .9z − 2.
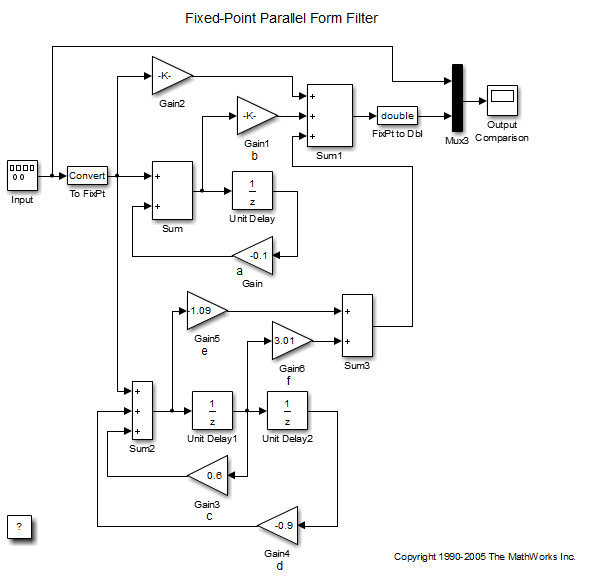
Реализация Hex (z) с использованием блоков Simulink ® с фиксированной точкой показана на следующем рисунке. Можно отобразить эту модель, введя
fxpdemo_parallel_form
в командной строке MATLAB ®.