В каноническом каскадном виде серии передаточная функция H (z) записывается как произведение передаточных функций первого порядка и второго порядка:
⋅H3 (z)... Hp (z).
Это уравнение дает каноническую каскадную форму ряда.
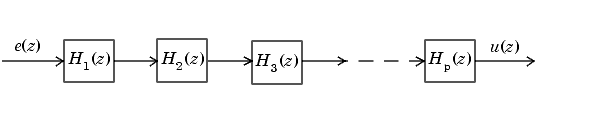
Факторинг H (z) в Hi (z), где i = 1,2,3,..., p может быть выполнен несколькими способами. Используя полюса и нули H (z), можно получить Hi (z), группируя пары сопряженных комплексных полюсов и пары сопряженных комплексных нулей для получения передаточных функций второго порядка, или группируя вещественные полюса и вещественные нули для получения передаточных функций первого или второго порядка. Можно также сгруппировать два вещественных нуля с парой сопряженных комплексных полюсов или наоборот. Поскольку существует много способов получения Hi (z), следует сравнить различные группировки, чтобы увидеть, что дает лучшие результаты для рассматриваемой передаточной функции.
Например, одной факторизацией H (z) может быть
− 1 + fiz − 21 + ciz − 1 + diz − 2.
Вы также должны принять во внимание, что порядок отдельных Hi (z)'s приведет к системам с различными числовыми характеристиками. Вы можете попробовать различные порядки для данного набора Hi (z) "s, чтобы определить, который дает лучшие числовые характеристики.
Ниже приведена диаграмма первого порядка для H (z).
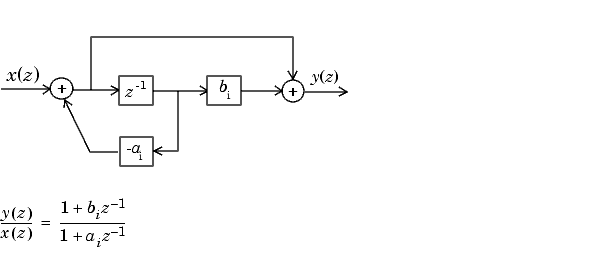
Ниже приведена диаграмма второго порядка для H (z).
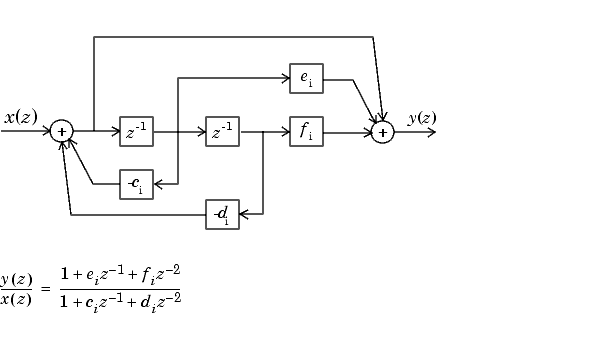
Последовательная каскадная форма примера передаточной функции задается
1z − 1) (1 − 0 .6z − 1 + 0 .9z − 2).
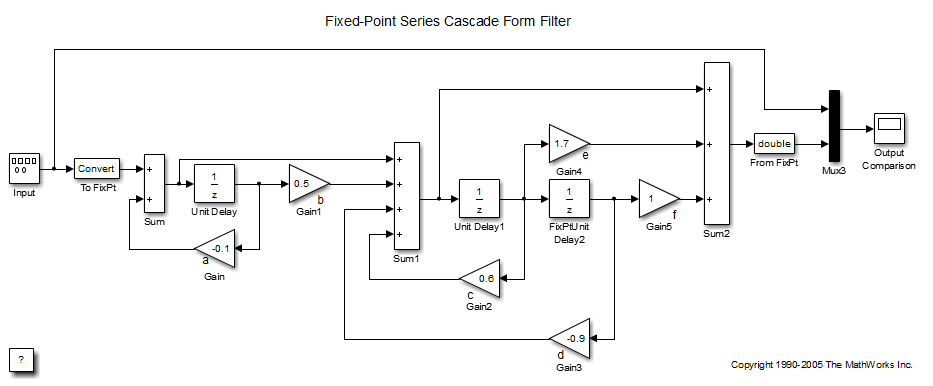
Реализация Hex (z) с использованием блоков Simulink ® с фиксированной точкой показана на следующем рисунке. Можно отобразить эту модель, введя
fxpdemo_series_cascade_form
в командной строке MATLAB ®.