Документация

Шаг 1. Определите проблему.

Проблема состоит в том, чтобы изменить положение и угол пушки для стрельбы снаряда как можно дальше за стеной. Пушка имеет дульную скорость 300 м/с. Высота стены - 20 м. Если пушка находится слишком близко к стене, она должна стрелять под слишком крутым углом, и снаряд недостаточно далеко движется. Если пушка находится слишком далеко от стены, снаряд также не проходит достаточно далеко.

Сопротивление воздуха замедляет снаряд. Сила сопротивления пропорциональна квадрату скорости с постоянной пропорциональности 0,02. На снаряд действует сила тяжести, разгоняющая его вниз при постоянных 9,81 ^м/с2. Следовательно, уравнения движения для траектории x (t) равны

где $$v(t\text{)}=dx(t$$)/dt.

Исходное положение x0 и начальная скорость xp0 являются 2-D векторами. Однако начальная высота x0(2) равно 0, поэтому начальное положение зависит только от скаляра x0(1). И начальная скорость xp0 имеет величину 300 (дульная скорость), поэтому зависит только от начального угла, скаляра. Для начального угла th, xp0 = 300*(cos(th),sin(th)). Поэтому задача оптимизации зависит только от двух скаляров, поэтому это задача 2-D. В качестве переменных принятия решения используйте расстояние по горизонтали и угол.

Шаг 2. Сформулируйте модель ОДУ.

Решатели ОДУ требуют, чтобы модель была сформулирована как система первого порядка. Увеличьте вектор траектории (x1 (t), x2 (t)) с его производной по времени ₍x '1 (_t), x' 2 (t)), чтобы сформировать вектор траектории 4-D. В терминах этого увеличенного вектора дифференциальное уравнение становится

Запишите дифференциальное уравнение как файл функции и сохраните его в пути MATLAB ®.

function f = cannonfodder(t,x)

f = [x(3);x(4);x(3);x(4)]; % Initial, gets f(1) and f(2) correct
nrm = norm(x(3:4)) * .02; % Norm of the velocity times constant
f(3) = -x(3)*nrm; % Horizontal acceleration
f(4) = -x(4)*nrm - 9.81; % Vertical acceleration

Визуализировать решение ОДУ, начиная с 30 м от стены под углом pi/3.

 Код для создания фигуры

x0 = [-30;0;300*cos(pi/3);300*sin(pi/3)];
sol = ode45(@cannonfodder,[0,10],x0);
% Find the time when the projectile lands
zerofnd = fzero(@(r)deval(sol,r,2),[sol.x(2),sol.x(end)]);
t = linspace(0,zerofnd); % equal times for plot
xs = deval(sol,t,1); % interpolated x values
ys = deval(sol,t,2); % interpolated y values
plot(xs,ys)
hold on
plot([0,0],[0,20],'k') % Draw the wall
xlabel('Horizontal distance')
ylabel('Trajectory height')
legend('Trajectory','Wall','Location','NW')
ylim([0 120])
hold off

Шаг 3. Решите с помощью поиска массива.

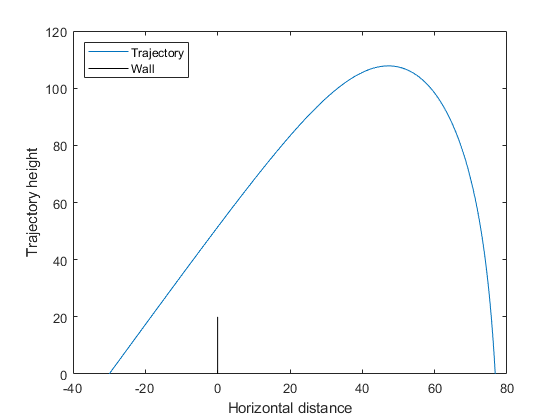
Проблема в том, чтобы найти исходное положение x0(1) и начальный угол x0(2) чтобы максимизировать расстояние от стены, на которую приземляется снаряд. Поскольку это проблема максимизации, минимизируйте отрицательное значение расстояния (см. раздел Максимизация по сравнению с минимизацией).

Использовать patternsearch для решения этой проблемы необходимо указать цель, ограничение, начальное предположение и опции.

Эти два файла являются функциями цели и ограничения. Скопируйте их в папку на вашем пути MATLAB.

function f = cannonobjective(x)
x0 = [x(1);0;300*cos(x(2));300*sin(x(2))];

sol = ode45(@cannonfodder,[0,15],x0);

% Find the time t when y_2(t) = 0
zerofnd = fzero(@(r)deval(sol,r,2),[sol.x(2),sol.x(end)]);
% Then find the x-position at that time
f = deval(sol,zerofnd,1);

f = -f; % take negative of distance for maximization



function [c,ceq] = cannonconstraint(x)

ceq = [];
x0 = [x(1);0;300*cos(x(2));300*sin(x(2))];

sol = ode45(@cannonfodder,[0,15],x0);

if sol.y(1,end) <= 0 % Projectile never reaches wall
    c = 20 - sol.y(2,end);
else
    % Find when the projectile crosses x = 0
    zerofnd = fzero(@(r)deval(sol,r,1),[sol.x(2),sol.x(end)]);
    % Then find the height there, and subtract from 20
    c = 20 - deval(sol,zerofnd,2);
end

Обратите внимание, что функции цели и ограничения задают свою входную переменную. x0 до 4-D начальной точки для решателя ОДУ. Решатель ОДУ не останавливается, если снаряд попадает в стенку. Вместо этого функция ограничения просто становится положительной, указывая на неосуществимое начальное значение.

Исходное положение x0(1) не может быть выше 0, и бесполезно иметь значение ниже -200. (Она должна быть около -20, потому что при отсутствии сопротивления воздуха самая длинная траектория будет начинаться с -20 под углом pi/4.) Аналогично, начальный угол x0(2) не может быть ниже 0 и не может быть выше pi/2. Установите границы немного в сторону от этих начальных значений:

lb = [-200;0.05];
ub = [-1;pi/2-.05];
x0 = [-30,pi/3]; % Initial guess

Установите UseCompletePoll опция для true. Это дает решение более высокого качества и обеспечивает прямое сравнение с параллельной обработкой, поскольку параллельные вычисления требуют этой настройки.

opts = optimoptions('patternsearch','UseCompletePoll',true);

Звонить patternsearch для решения проблемы.

tic % Time the solution
[xsolution,distance,eflag,outpt] = patternsearch(@cannonobjective,x0,...
    [],[],[],[],lb,ub,@cannonconstraint,opts)
toc

Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.

xsolution =

  -28.8123    0.6095


distance =

 -125.9880


eflag =

     1


outpt = 

  struct with fields:

         function: @cannonobjective
      problemtype: 'nonlinearconstr'
       pollmethod: 'gpspositivebasis2n'
    maxconstraint: 0
     searchmethod: []
       iterations: 5
        funccount: 269
         meshsize: 8.9125e-07
         rngstate: [1×1 struct]
          message: 'Optimization terminated: mesh size less than options.MeshTolerance↵ and constraint violation is less than options.ConstraintTolerance.'

Elapsed time is 0.792152 seconds.

Запуск снаряда примерно в 29 м от стенки под углом 0,6095 радиан приводит к самому дальнему расстоянию, около 126 м. Заявленное расстояние является отрицательным, потому что целевая функция является отрицательной от расстояния до стенки.

Визуализация решения.

x0 = [xsolution(1);0;300*cos(xsolution(2));300*sin(xsolution(2))];

sol = ode45(@cannonfodder,[0,15],x0);
% Find the time when the projectile lands
zerofnd = fzero(@(r)deval(sol,r,2),[sol.x(2),sol.x(end)]);
t = linspace(0,zerofnd); % equal times for plot
xs = deval(sol,t,1); % Interpolated x values
ys = deval(sol,t,2); % Interpolated y values
plot(xs,ys)
hold on
plot([0,0],[0,20],'k') % Draw the wall
xlabel('Horizontal distance')
ylabel('Trajectory height')
legend('Trajectory','Wall','Location','NW')
ylim([0 70])
hold off

Шаг 4. Избегайте двойного вызова дорогостоящей подпрограммы.

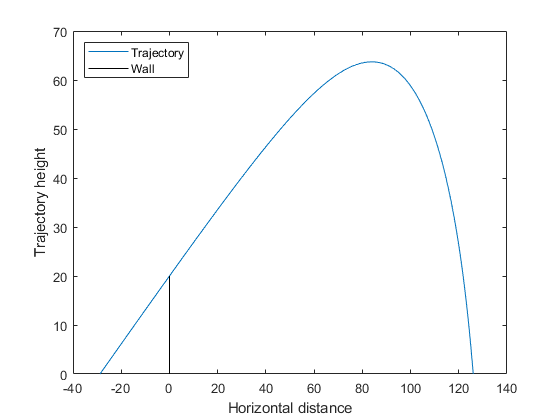
Как целевая, так и нелинейная функция ограничения вызывают решатель ОДУ для вычисления их значений. Чтобы избежать двойного вызова решателя, используйте методику, описанную в разделе Целевые и нелинейные ограничения в одной и той же функции. runcannon файл реализует этот метод. Скопируйте этот файл в папку на вашем пути MATLAB.

function [x,f,eflag,outpt] = runcannon(x0,opts)

if nargin == 1 % No options supplied
    opts = [];
end

xLast = []; % Last place ode solver was called
sol = []; % ODE solution structure

fun = @objfun; % The objective function, nested below
cfun = @constr; % The constraint function, nested below

lb = [-200;0.05];
ub = [-1;pi/2-.05];

% Call patternsearch
[x,f,eflag,outpt] = patternsearch(fun,x0,[],[],[],[],lb,ub,cfun,opts);

    function y = objfun(x)
        if ~isequal(x,xLast) % Check if computation is necessary
            x0 = [x(1);0;300*cos(x(2));300*sin(x(2))];
            sol = ode45(@cannonfodder,[0,15],x0);
            xLast = x;
        end
        % Now compute objective function
        % First find when the projectile hits the ground
        zerofnd = fzero(@(r)deval(sol,r,2),[sol.x(2),sol.x(end)]);
        % Then compute the x-position at that time
        y = deval(sol,zerofnd,1);
        y = -y; % take negative of distance
    end

    function [c,ceq] = constr(x)
       ceq = [];
        if ~isequal(x,xLast) % Check if computation is necessary
            x0 = [x(1);0;300*cos(x(2));300*sin(x(2))];
            sol = ode45(@cannonfodder,[0,15],x0);
            xLast = x;
        end
        % Now compute constraint functions
        % First find when the projectile crosses x = 0
        zerofnd = fzero(@(r)deval(sol,r,1),[sol.x(1),sol.x(end)]);
        % Then find the height there, and subtract from 20
        c = 20 - deval(sol,zerofnd,2);
    end

end

Повторная инициализация проблемы и время вызова runcannon.

x0 = [-30;pi/3];
tic
[xsolution,distance,eflag,outpt] = runcannon(x0,opts);
toc

Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.
Elapsed time is 0.670715 seconds.

Решатель работал быстрее, чем раньше. При анализе решения видно, что выходные данные идентичны.

Шаг 5. Вычислять параллельно.

Попробуйте сэкономить больше времени, вычисляя параллельно. Начните с открытия параллельного пула работников.

parpool

Starting parpool using the 'local' profile ...
Connected to the parallel pool (number of workers: 6).

ans = 

 ProcessPool with properties: 

            Connected: true
           NumWorkers: 6
              Cluster: local
        AttachedFiles: {}
    AutoAddClientPath: true
          IdleTimeout: 30 minutes (30 minutes remaining)
          SpmdEnabled: true

Задайте параметры для использования параллельных вычислений и повторно запустите решатель.

opts = optimoptions('patternsearch',opts,'UseParallel',true);
x0 = [-30;pi/3];
tic
[xsolution,distance,eflag,outpt] = runcannon(x0,opts);
toc

Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.
Elapsed time is 1.894515 seconds.

В этом случае параллельные вычисления были медленнее. При анализе решения видно, что выходные данные идентичны.

Шаг 6. Сравните с генетическим алгоритмом.

Также можно попытаться решить проблему с помощью генетического алгоритма. Однако генетический алгоритм обычно более медленный и менее надежный.

Как объясняется в разделе Объективные и нелинейные ограничения в одной и той же функции, нельзя экономить время при использовании ga по методу вложенной функции, используемому patternsearch на шаге 4. Вместо этого звоните ga параллельно путем установки соответствующих параметров.

options = optimoptions('ga','UseParallel',true);
rng default % For reproducibility
tic % Time the solution
[xsolution,distance,eflag,outpt] = ga(@cannonobjective,2,...
    [],[],[],[],lb,ub,@cannonconstraint,options)
toc

Optimization terminated: average change in the fitness value less than options.FunctionTolerance
 and constraint violation is less than options.ConstraintTolerance.

xsolution =

  -37.6217    0.4926


distance =

 -122.2181


eflag =

     1


outpt = 

  struct with fields:

      problemtype: 'nonlinearconstr'
         rngstate: [1×1 struct]
      generations: 4
        funccount: 9874
          message: 'Optimization terminated: average change in the fitness value less than options.FunctionTolerance↵ and constraint violation is less than options.ConstraintTolerance.'
    maxconstraint: 0
       hybridflag: []

Elapsed time is 12.529131 seconds.

ga решение не так хорошо, как patternsearch раствор: 122 м против 126 м. ga занимает больше времени: около 12 с против менее 2 с; patternsearch занимает еще меньше времени в последовательном и вложенном, менее 1 с. Выполнение ga серийно занимает еще больше времени, около 30 с за один тестовый прогон.