Генетический алгоритм применяет мутации с использованием MutationFcn вариант. Вариант мутации по умолчанию, @mutationgaussian, добавляет случайное число, или мутацию, выбранную из гауссова распределения, к каждой записи родительского вектора. Обычно количество мутации, которое пропорционально стандартному отклонению распределения, уменьшается у каждого нового поколения. Можно управлять средним количеством мутаций, которое алгоритм применяет к родительскому объекту в каждом поколении, с помощью Scale и Shrink входные данные, которые включаются в массив ячеек:
options = optimoptions('ga',... 'MutationFcn',{@mutationgaussian Scale Shrink});
Scale и Shrink скаляры со значениями по умолчанию 1 каждый.
Scale контролирует стандартное отклонение мутации в первом поколении. Это значение равно Scale умножается на диапазон начального заполнения, который задается параметром InitialPopulationRange вариант.
Shrink контролирует скорость, с которой среднее количество мутации уменьшается. Стандартное отклонение линейно уменьшается, так что его конечное значение равно 1 - Усадка умножает его начальное значение в первом поколении. Например, если Shrink имеет значение по умолчанию 1затем количество мутации уменьшается до 0 на конечной стадии.
Вы можете увидеть эффект мутации, выбрав функции графика @gaplotdistance и @gaplotrange, а затем запуск генетического алгоритма над проблемой, такой как та, которая описана в «Минимизировать функцию Растригина». На следующем рисунке показан график после установки генератора случайных чисел.
rng default % For reproducibility options = optimoptions('ga','PlotFcn',{@gaplotdistance,@gaplotrange},... 'MaxStallGenerations',200); % to get a long run [x,fval] = ga(@rastriginsfcn,2,[],[],[],[],[],[],[],options);
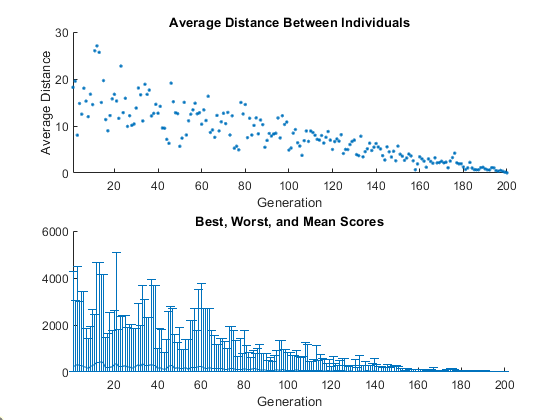
На верхнем графике отображается среднее расстояние между точками в каждом поколении. По мере уменьшения количества мутации уменьшается и среднее расстояние между индивидуумами, которое приблизительно равно 0 в конечном поколении. На нижнем графике отображается вертикальная линия в каждом поколении, показывающая диапазон от наименьшего до наибольшего значения фитнеса, а также среднее значение фитнеса. По мере уменьшения количества мутации уменьшается и диапазон. Эти графики показывают, что уменьшение количества мутаций уменьшает разнообразие последующих поколений.
Для сравнения на следующем рисунке показаны те же самые графики при установке Shrink кому 0.5.
options = optimoptions('ga',options,... 'MutationFcn',{@mutationgaussian,1,.5}); [x,fval] = ga(@rastriginsfcn,2,[],[],[],[],[],[],[],options);
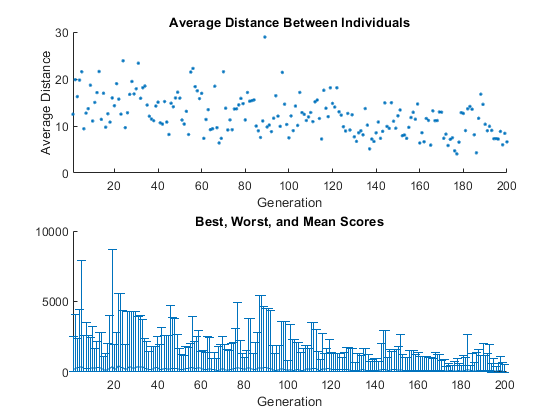
На этот раз среднее количество мутации уменьшается в 1/2 раза к конечному поколению. В результате среднее расстояние между особями уменьшается меньше, чем раньше.
CrossoverFraction параметр определяет долю каждого населения, кроме элитных детей, которые состоят из перекрестных детей. Доля кроссовера 1 означает, что все дети, кроме элитных лиц, являются детьми-кроссоверами, в то время как доля кроссоверов 0 означает, что все дети являются детьми мутации. Следующий пример показывает, что ни одна из этих крайностей не является эффективной стратегией оптимизации функции.
В примере используется функция пригодности, значение которой в точке является суммой абсолютных значений координат в точках. То есть
=|x1|+|x2|+⋯+|xn|.
Эту функцию можно определить как анонимную, установив для нее значение
@(x) sum(abs(x))
Выполните пример со значением по умолчанию 0.8 в качестве CrossoverFraction вариант.
fun = @(x) sum(abs(x)); nvar = 10; options = optimoptions('ga',... 'InitialPopulationRange',[-1;1],... 'PlotFcn',{@gaplotbestf,@gaplotdistance}); rng(14,'twister') % For reproducibility [x,fval] = ga(fun,nvar,[],[],[],[],[],[],[],options)
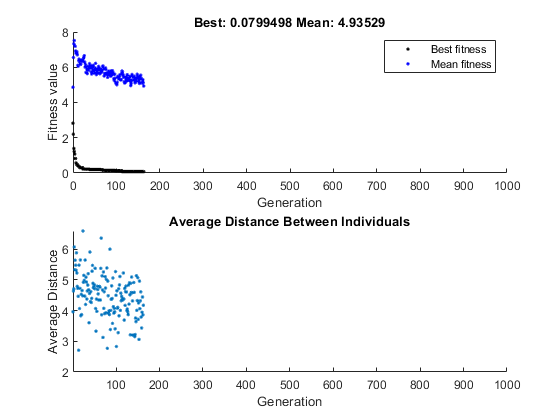
Optimization terminated: average change in the fitness value less than options.FunctionTolerance.
x =
-0.0020 -0.0134 -0.0067 -0.0028 -0.0241 -0.0118 0.0021 0.0113 -0.0021 -0.0036
fval =
0.0799Чтобы увидеть, как генетический алгоритм работает, когда нет мутации, установите CrossoverFraction опция для 1.0 и повторно запустите решатель.
options.CrossoverFraction = 1; [x,fval] = ga(fun,nvar,[],[],[],[],[],[],[],options)
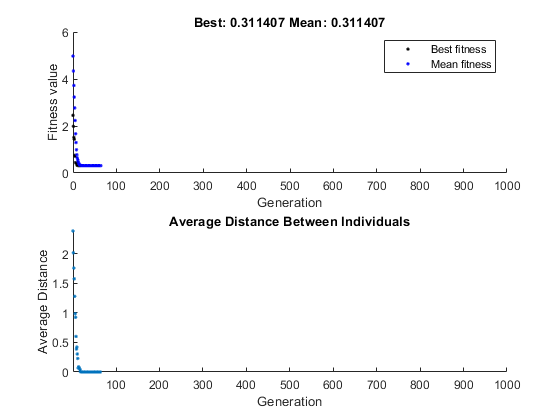
x =
-0.0275 -0.0043 0.0372 -0.0118 -0.0377 -0.0444 -0.0258 -0.0520 0.0174 0.0533
fval =
0.3114Optimization terminated: average change in the fitness value less than options.FunctionTolerance. x = 0.4014 0.0538 0.7824 0.1930 0.0513 -0.4801 0.9988 -0.0059 0.0875 0.0302 fval = 3.0843
В этом случае алгоритм выбирает гены из индивидуумов в начальной популяции и рекомбинирует их. Алгоритм не может создать новые гены, так как нет мутации. Алгоритм генерирует лучшего человека, который может использовать эти гены в поколении № 8, где лучший график фитнеса становится ровным. После этого он создает новые копии лучшего индивидуума, которые затем выбираются для следующего поколения. По поколению № 17 все особи в популяции одинаковы, а именно - лучшая особь. Когда это происходит, среднее расстояние между особями равно 0. Поскольку алгоритм не может улучшить наилучшее значение фитнеса после поколения 8, он останавливается еще после 50 поколений, потому что поколения Stall установлены на 50.
Чтобы увидеть, как работает генетический алгоритм, когда нет кроссовера, установите CrossoverFraction опция для 0.
options.CrossoverFraction = 0; [x,fval] = ga(fun,nvar,[],[],[],[],[],[],[],options)
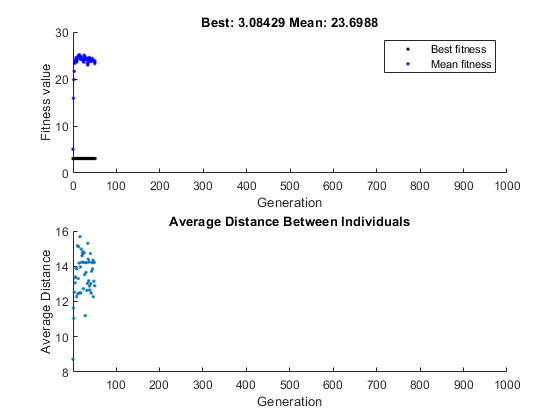
В этом случае случайные изменения, которые применяет алгоритм, никогда не улучшают пригодность лучшего индивидуума в первом поколении. В то время как он улучшает отдельные гены других индивидуумов, как можно видеть на верхнем графике по снижению среднего значения фитнес-функции, эти улучшенные гены никогда не объединяются с генами лучшего индивидуума, потому что нет кроссовера. В итоге лучшим фитнес-сюжетом становится уровень и алгоритм застопоривается на генерацию номер 50.
Пример deterministicstudy.m, который включен в программное обеспечение, сравнивает результаты применения генетического алгоритма к функции Растригина с CrossoverFraction параметр имеет значение 0, .2, .4, .6, .8, и 1. Пример работает в течение 10 поколений. В каждом поколении в примере показаны средние и стандартные отклонения наилучших значений пригодности во всех предыдущих поколениях для каждого значения CrossoverFraction вариант.
Для выполнения примера введите
deterministicstudy
в подсказке MATLAB ®. По завершении примера графики отображаются так, как показано на следующем рисунке.
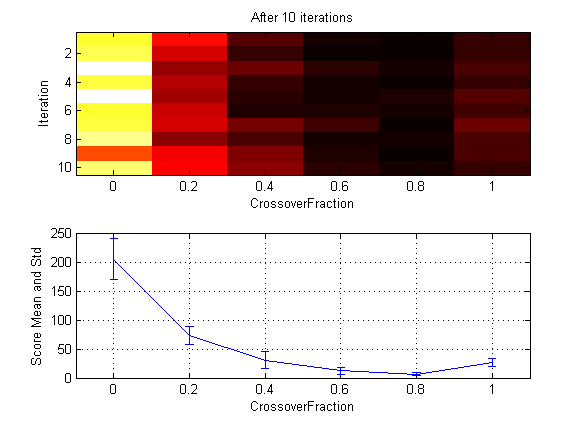
На нижнем графике показаны средние и стандартные отклонения лучших значений пригодности за 10 поколений, для каждого из значений кроссоверной фракции. Верхний график показывает цветовое отображение лучших значений пригодности в каждом поколении.
Для этой функции фитнеса установите фракцию Crossover на 0.8 дает лучший результат. Однако для другой функции фитнеса другой параметр для фракции Crossover может дать наилучший результат.