Преобразование Радона

Примечание

Сведения о создании данных проекции из интегралов линий вдоль траекторий, излучаемых из одного источника, называемых проекциями веер-пучков, см. в разделе Проекция веер-пучков. Для преобразования данных проекции параллельного луча в данные проекции вентиляторного луча используйте para2fan функция.

radon функция вычисляет проекции матрицы изображения вдоль заданных направлений.

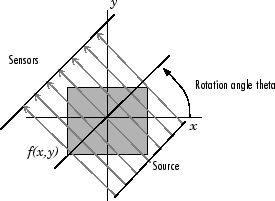
Проекция двумерной функции f (x, y) представляет собой множество линейных интегралов. radon функция вычисляет интегралы линий из нескольких источников вдоль параллельных траекторий, или пучков, в определенном направлении. Пучки разнесены на 1 пиксел. Чтобы представить изображение, radon функция принимает множество параллельных лучевых проекций изображения под разными углами путем поворота источника вокруг центра изображения. На следующем рисунке показан одиночный выступ с заданным углом поворота.

Проекция параллельной балки при угле поворота тета

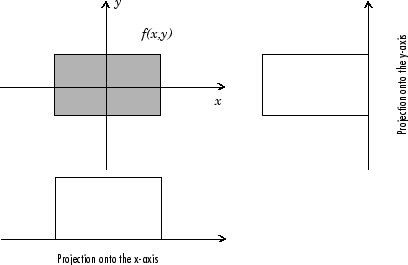
Например, линейный интеграл f (x, y) в вертикальном направлении представляет собой проекцию f (x, y) на ось x; линия, интегральная в горизонтальном направлении, представляет собой проекцию f (x, y) на ось y. На следующем рисунке показаны горизонтальные и вертикальные проекции для простой двумерной функции.

Горизонтальные и вертикальные проекции простой функции

Проекции могут быть вычислены вдоль любого угла theta (start). В общем, преобразование Радона f (x, y) является линейным интегралом f, параллельным оси y '

$_{Rstart(} x')_{}^{} =\int-\infty\inftyf (x'cosθ-y'sinθ,x'sinθ+y'cosθ$ ) dy ′

где

$[\begin{matrix} x′y \end{matrix}'] \begin{matrix} = [ \\ cosunsinü − \end{matrix} \begin{matrix} sinü cosstart \end{matrix}]$ [xy]

На следующем рисунке показана геометрия преобразования Радона.

Геометрия преобразования Радона

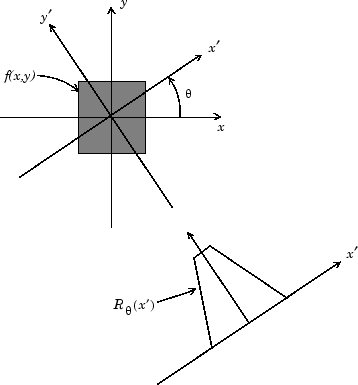
Постройте график преобразования Радона изображения

Открыть сценарий в реальном времени

В этом примере показано, как вычислить преобразование Радона изображения, I, для конкретного набора углов, theta, с использованием radon функция. Функция возвращает, R, в котором столбцы содержат преобразование Радона для каждого угла в theta. Функция также возвращает вектор, xp , который содержит соответствующие координаты вдоль оси X. Центральный пиксель I определено как floor((size(I)+1)/2), который является пикселем на оси x, соответствующей x '= 0.

Создайте небольшой образец изображения для этого примера, состоящего из одного квадратного объекта, и отобразите его.

I = zeros(100,100);
I(25:75,25:75) = 1;
imshow(I)

Figure contains an axes. The axes contains an object of type image.

Вычислите преобразование Радона изображения для углов 0 градусов и 45 градусов.

[R,xp] = radon(I,[0 45]);

Постройте график преобразования для 0 градусов.

figure
plot(xp,R(:,1));
title('Radon Transform of a Square Function at 0 degrees')

Figure contains an axes. The axes with title Radon Transform of a Square Function at 0 degrees contains an object of type line.

Постройте график преобразования для 45 градусов.

figure
plot(xp,R(:,2)); 
title('Radon Transform of a Square Function at 45 degrees')

Figure contains an axes. The axes with title Radon Transform of a Square Function at 45 degrees contains an object of type line.

Просмотр преобразования Радона как изображения

Преобразование Радона для большого количества углов часто отображается как изображение. В этом примере преобразование Радона для квадратного изображения вычисляется под углами от 0 ° до 180 ° с шагом 1 °.

theta = 0:180;
[R,xp] = radon(I,theta);
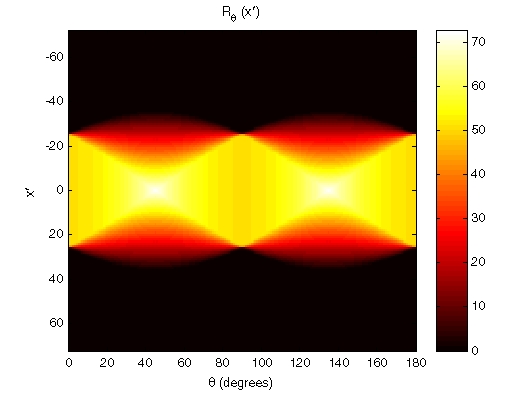
imagesc(theta,xp,R);
title('R_{\theta} (X\prime)');
xlabel('\theta (degrees)');
ylabel('X\prime');
set(gca,'XTick',0:20:180);
colormap(hot);
colorbar

Преобразование Радона с использованием 180 проекций

Документация