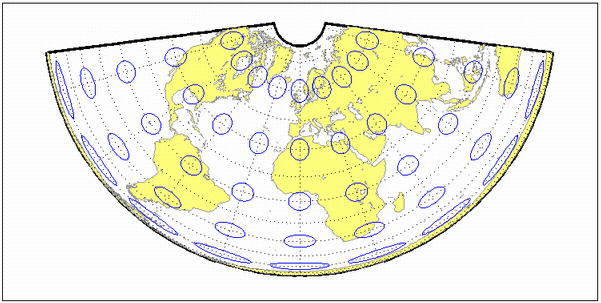
Коническая проекция Albers равной площади - стандарт
Конический
eqaconicstd
Меридианы: Равноудаленные прямые, сходящиеся к общей точке, обычно за полюсом. Углы между меридианами меньше истинных углов.
Параллели: неравноотстоящие концентрические дуги окружности, центрированные в точке схождения. Расстояние между параллелями уменьшается в сторону от центральных широт.
Полюса: Обычно круглые дуги, охватывающие тот же угол, что и отображаемые параллели.
Симметрия: О любом меридиане.
Эта функция реализует коническую проекцию Albers Equal Area непосредственно на опорном эллипсоиде, что соответствует отраслевому определению этой проекции. Посмотрите eqaconic для альтернативной реализации, основанной на ротации авторской сферы.
Это проекция равной площади. Масштаб соответствует одному или двум выбранным стандартным параллелям. Масштаб постоянен вдоль любой параллели; масштабный коэффициент меридиана в любой заданной точке является взаимностью этого коэффициента вдоль параллели для сохранения равной площади. Проекция свободна от искажений по стандартным параллелям. Искажение является постоянным вдоль любой другой параллели. Эта проекция не является ни конформной, ни равноудаленной.
Конус проекции имеет интересные ограничивающие формы. Если полюс выбран в качестве одной стандартной параллели, конус является плоскостью, и в результате получается проекция равной площади Ламберта Азимутала. Если выбраны две параллели, не симметричные относительно экватора, то получается коническая проекция равной площади Ламберта. Если полюс выбран в качестве одного из стандартных параллелей, то проецируемый полюс является точкой, в противном случае проецируемый полюс является дугой. Если экватор выбран в виде одной параллели, конус становится цилиндром, и результатом является цилиндрическая проекция равной площади Ламберта. Наконец, если в качестве стандартных параллелей выбраны две параллели, равноудаленные от экватора, результатом будет цилиндрическая проекция Бермана или другой цилиндрической проекции равной площади. Предлагаемые параллели для карт изобилия США - [29.5 45.5]. Параллели по умолчанию - [15 75].
Эта проекция была представлена Генрихом Кристианом Альберсом в 1805 году и также известна как коническая ортоморфная проекция. Конус проекции имеет интересные ограничивающие формы. Если полюс выбран в качестве одной стандартной параллели, конус является плоскостью, и результатом является коническая проекция равной площади Ламберта. Если экватор выбран как одна параллель, конус становится цилиндром, и результатом является цилиндрическая проекция равной площади Ламберта. Наконец, если в качестве стандартных параллелей выбраны две параллели, равноудаленные от экватора, результатом является проекция Бермана или другая цилиндрическая проекция равной площади.
Toolbox™ картографирования использует другую реализацию стандартной конической проекции равной площади Альберса для отображения координат на осях карты, чем для проецирования координат с помощью projfwd или projinv функция. Эти реализации могут давать различные результаты.
landareas = shaperead('landareas.shp','UseGeoCoords',true);
axesm ('eqaconicstd', 'Frame', 'on', 'Grid', 'on');
geoshow(landareas,'FaceColor',[1 1 .5],'EdgeColor',[.6 .6 .6]);
tissot;