Документация

Измерить площадь сферических четырехугольников

В твердотельной геометрии площадь сферического четырехугольника может быть точно рассчитана. Сферический четырёхугольник - пересечение лунки и зоны. В географическом отношении четырёхугольник определяется как область, ограниченная параллелями север и юг, и меридианами восток и запад.

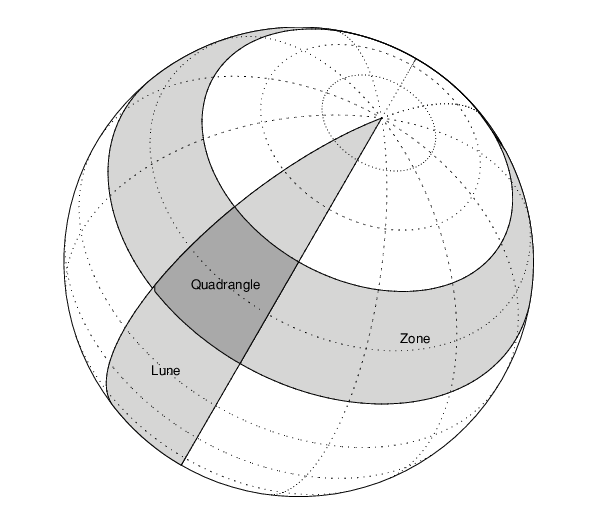
В изображенном примере четырёхугольник образован пересечением зоны, представляющей собой область, ограниченную 15 ° N и 45 ° N широтами, и лунки, представляющей собой область, ограниченную 0 ° и 30 ° E долготой. При предположении сферической планеты можно вычислить долю всей площади сферической поверхности, вписанной в четырёхугольник:

area = areaquad(15,0,45,30)

area =
  	0.0187

То есть менее 2% площади поверхности планеты находится в этом четырёхугольнике. Чтобы получить абсолютную цифру, например, в квадратных милях, необходимо указать соответствующий сферический радиус. Радиус Земли составляет около 3958,9 миль:

area = areaquad(15,0,45,30,3958.9)

area =
     3.6788e+06

Площадь поверхности в этом четырехугольнике составляет более 3,6 миллиона квадратных миль для сферической Земли.