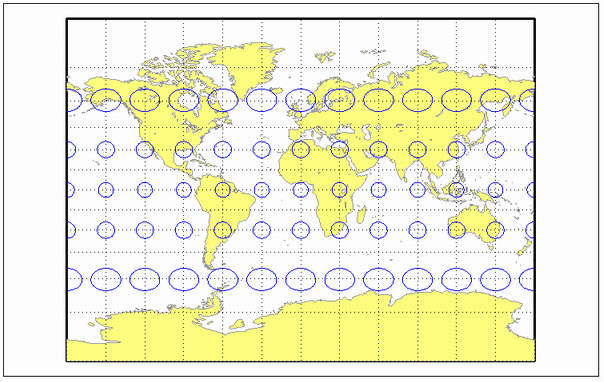
Цилиндрическая проекция Мельника
Цилиндрический
miller
Меридианы: Равноудаленные прямые параллельные линии 0,73 до экватора.
Параллели: Неравноотстоящие прямые параллельные линии, перпендикулярные меридианам. Расстояние увеличивается к полюсам, менее быстро, чем у проекции Меркатора.
Полюса: Прямые линии, равные по длине экватору.
Симметрия: О любом меридиане или экваторе.
Это проекция с параллельным интервалом, рассчитанным для сохранения внешнего вида, аналогичного проекции Меркатора, при одновременном уменьшении искажения вблизи полюсов и обеспечении возможности отображения полюсов. Она не равна площади, равноудалена, конформна или перспективна. Шкала верна вдоль экватора и постоянна между двумя параллелями, равноудалёнными от экватора. Вблизи Экватора нет искажения, и оно умеренно увеличивается вдали от Экватора, но на полюсах становится сильным.
Цилиндрическая проекция Миллера получена из проекции Меркатора; параллели отстоят от экватора вычислением расстояния на Меркаторе для параллели на 80% истинной широты и делением результата на 0,8. В результате две проекции почти идентичны вблизи экватора.
Для цилиндрических выступов задана только одна стандартная параллель. Другая стандартная параллель - та же широта с противоположным знаком. Для этой проекции стандартная параллель по определению зафиксирована на 0 °.
Эта проекция была представлена Осборном Мейтлендом Миллером из Американского географического общества в 1942 году. Он часто используется вместо проекции Меркатора для атласных карт мира, для которых он несколько более уместен.
Toolbox™ отображения использует другую реализацию проекции Миллера для отображения координат на осях карты, чем для проецирования координат с помощью projfwd или projinv функция. Эти реализации могут давать различные результаты.
Реализация проекции Миллера для отображения координат на осях карты применима только для координат, связанных со сферой. Реализация проекции Миллера для проецирования координат с использованием projfwd или projinv функция применима для координат, связанных со сферой или эллипсоидом.
landareas = shaperead('landareas.shp','UseGeoCoords',true);
axesm ('miller', 'Frame', 'on', 'Grid', 'on');
geoshow(landareas,'FaceColor',[1 1 .5],'EdgeColor',[.6 .6 .6]);
tissot;