Географические объекты, представленные векторными данными, могут быть или не быть отформатированы как многоугольники. Представьте себе две переменные, latcoast и loncoast, которые соответствуют последовательности точек, которые карикатурны на побережье острова Великобритания. Если эти данные возвращаются к своей начальной точке, то полигон, описывающий Великобританию, существует. Эти данные могут быть нанесены на график как фрагмент или как линия, и они могут быть логически использованы в расчетах как.
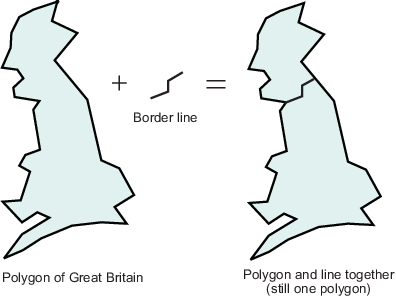
Теперь предположим, что вы хотите представлять англо-шотландскую границу, от западного побережья в Солуэй-Ферт до восточного побережья в Бервик-на-Твиде. Эти данные можно правильно определить только как прямую, определяемую двумя или более точками, которые можно представить с помощью двух переменных, latborder и lonborder. При совместной печати две пары переменных могут формировать карту. Патч Великобритании плюс линия, показывающая шотландскую границу, может выглядеть как два патча или области, но нет объекта, который представляет Англию, и нет объекта, который представляет Шотландию, ни в рабочем пространстве, ни на топорах карты.
Чтобы правильно представлять оба региона, полигон Великобритании необходимо разделить в двух точках, где граница его встречает, и копию latborder и lonborder конкатенация с обеими линиями (размещение одной в обратном порядке). Полученные два многоугольника могут быть представлены отдельно (например, в четырех переменных, названных latengland, lonengland, latscotland, и lonscotland) или в двух переменных, которые определяют два многоугольника каждая, очерченных NaNs (например, latuk, lonuk).
Различие между линейными и многоугольными данными может показаться неважным, но оно может иметь значение при выполнении географического анализа и тематического картирования. Например, данные полигонов могут обрабатываться как линейные данные и отображаться с такими функциями, как linem, но данные линии не могут обрабатываться как многоугольники, если они не реструктурированы, чтобы сделать все объекты близкими друг к другу, как описано в разделе «Связать сегменты линии с общими конечными точками в многоугольники».