Хотя Земля очень круглая, она является сплюснутым сфероидом, а не совершенной сферой. Эта разница настолько мала (только одна часть в 300), что моделирования Земли как сферической достаточно для составления мелкомасштабных (мировых или континентальных) карт. Однако создание точных карт в больших масштабах требует использования сфероидальной модели. Такие модели необходимы, например, при картировании спутниковых или воздушных снимков высокого разрешения или при работе с координатами Глобальной системы позиционирования (GPS). В этом разделе рассматривается, как программное обеспечение Mapping Toolbox™ точно моделирует форму или фигуру Земли.
Эллипсоиды можно определить несколькими способами. Они обычно задаются полумажем и осью полуминора, но часто выражаются в терминах большой полумажной оси и либо обратного сплющивания (которое для Земли, как упоминалось выше, является одной частью в 300), либо эксцентриситета. Какие бы параметры ни использовались, до тех пор, пока включена длина оси, эллипсоид полностью ограничен, а другие параметры могут быть получены. Компоненты эллипсоида показаны на следующей диаграмме.
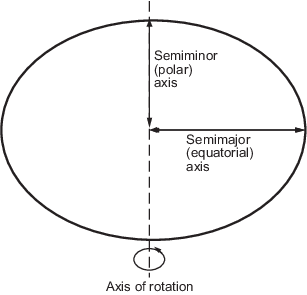
Инструментарий включает эллипсоидные модели, которые представляют фигуры Солнца, Луны и планет, а также набор наиболее распространенных эллипсоидных моделей Земли. Дополнительные сведения см. в разделе Справочные сфероиды.
Буквально геоид означает земную форму. Геоид - эмпирическое приближение фигуры Земли (минус топографический рельеф), её «комковатость». В частности, это эквипотенциальная поверхность относительно гравитации, более или менее соответствующая среднему уровню моря. Это приблизительно эллипсоид, но не совсем так, потому что локальные вариации гравитации создают незначительные холмы и далы (которые варьируются от -100 м до + 60 м по всей Земле). Это изменение высоты составляет порядка 1 процента от различий между большой и эллипсоидной полуосями, используемых для аппроксимации формы Земли.
Форма геоида важна для некоторых целей, таких как расчет орбит спутников, но не обязательно должна учитываться для каждого приложения картографирования. Однако знание геоида иногда необходимо, например, при сравнении отметок, заданных как высота над средним уровнем моря, с отметками, полученными из измерений GPS. Геоидные представления также присущи определениям опорных элементов.
Получение высоты геоида и объекта привязки географических проводок из модели геоида EGM96. Данные о широте и долготе береговой линии.
[N,R] = egm96geoid;
load coastlinesОтображение высоты геоида в виде поверхности с помощью проекции Робинсона. Убедитесь, что данные береговой линии отображаются на поверхности, установив 'CData' пара имя-значение к данным высоты геоида и 'ZData' пара имя-значение к матрице нулей. Затем просмотрите данные береговой линии.
axesm robinson Z = zeros(R.RasterSize); geoshow(N,R,'DisplayType','surface','CData',N,'ZData',Z) geoshow(coastlat,coastlon,'color','k')
Отображение цветовой полосы под картой.
colorbar('southoutside')