Совместимые размеры массивов для основных операций

Большинство двоичных операторов и функций в MATLAB ® поддерживают числовые массивы совместимых размеров. Два входа имеют совместимые размеры, если для каждого размера размеры входов одинаковы или один из них равен 1. В простейших случаях два размера массива совместимы, если они точно одинаковы или один является скаляром. MATLAB неявно расширяет массивы совместимых размеров до одинакового размера во время выполнения операции или функции по элементам.

Входы с совместимыми размерами

2-D Входы

Это некоторые комбинации скаляров, векторов и матриц, которые имеют совместимые размеры:

Два входа, которые имеют одинаковый размер.
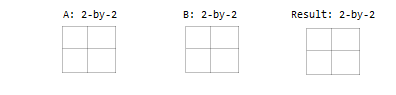
Один вход - скаляр.
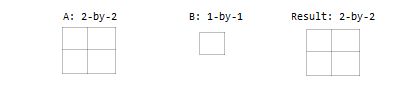
Один вход является матрицей, а другой - вектором столбца с таким же количеством строк.
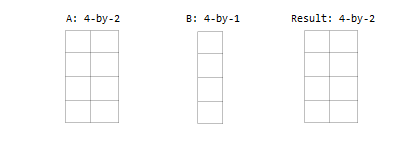
Один вход является вектором столбца, а другой - вектором строки.

Многомерные массивы

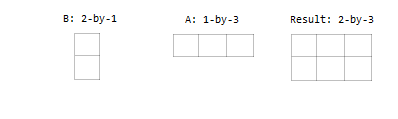
Каждый массив в MATLAB имеет конечные размеры размера 1. Для многомерных множеств это означает, что матрица 3 на 4 совпадает с матрицей размера 3 на 4 на 1 на 1 на 1. Примерами многомерных массивов с совместимыми размерами являются:

Один вход является матрицей, а другой - 3-D массивом с таким же количеством строк и столбцов.
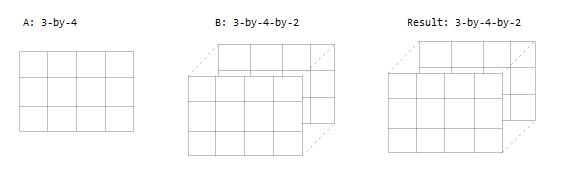
Один вход является матрицей, а другой - 3-D массивом. Все размеры одинаковы или один из них равен 1.

Пустые массивы

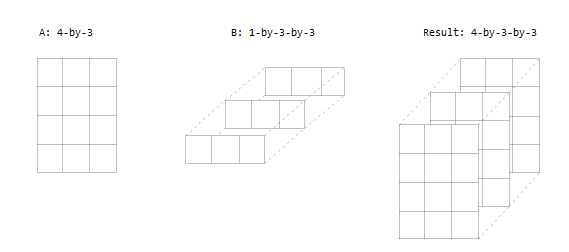
Правила одинаковы для пустых массивов или массивов с нулевым размером измерения. Размер размера, который не равен 1, определяет размер вывода. Это означает, что размеры с нулевым размером должны быть спарены с размером 1 или 0 в другом массиве, и что выходные данные имеют размер 0.

     A: 1-by-0     
     B: 3-by-1
Result: 3-by-0

Входы с несовместимыми размерами

Несовместимые входные данные имеют размеры, которые не могут быть неявно расширены до одинакового размера. Например:

Один из размеров не равен и не равен 1.
```
A: 3-by-2
B: 4-by-2
```
Два нескалярных вектора строк с разными длинами.
```
A: 1-by-3
B: 1-by-4
```

Примеры

Вычесть вектор из матрицы

Чтобы упростить векторно-матричные операции, используйте неявное расширение с размерными функциями, такими как sum, mean, minи другие.

Например, вычислите среднее значение каждого столбца в матрице, затем вычтите среднее значение из каждого элемента.

A = magic(3)

A =

     8     1     6
     3     5     7
     4     9     2

C = mean(A)

C =

     5     5     5

A - C

ans =

     3    -4     1
    -2     0     2
    -1     4    -3

Добавить вектор строки и столбца

Векторы строк и столбцов имеют совместимые размеры, и при выполнении операции над ними результатом является матрица.

Например, добавьте вектор строки и столбца. Результат такой же, как bsxfun(@plus,a,b).

a = [1 2 3 4]

ans =

     1     2     3     4

b = [5; 6; 7]

a + b

ans =

     6     7     8     9
     7     8     9    10
     8     9    10    11

См. также

bsxfun

Документация