Exponenta Banner
exponenta event banner

несетка

Преобразование рёберной матрицы в координатную и лапласовскую матрицы

Синтаксис

[L,XY] = unmesh(E)

Описание

[L,XY] = unmesh(E) возвращает матрицу Лапласа L и матрица координат вершин сетки XY для M-на-4 граничная матрица E. Каждая строка матрицы ребер должна содержать координаты [x1 y1 x2 y2] конечных точек кромки.

Входные аргументы

EM-by-4 матрица ребер E.

Выходные аргументы

LЛапласианское матричное представление графа.
XYМатрица координат вершин сетки.

Примеры

Возьмем простой пример квадрата с вершинами (1,1), (1, -1), (-1, -1) и (-1,1), где соединения между вершинами являются четырьмя перпендикулярными рёбрами квадрата плюс одно диагональное соединение между (-1, -1) и ( 1,1).

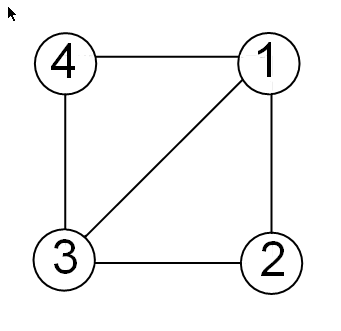
Матрица ребер E для этого графика:

E = [1  1  1 -1;  % edge from 1 to 2
     1 -1 -1 -1;  % edge from 2 to 3 
    -1 -1 -1  1;  % edge from 3 to 4
    -1 -1  1  1;  % edge from 3 to 1
    -1  1  1  1]  % edge from 4 to 1
Использовать unmesh для создания матрицы координат Лапласа и сетки из списка кромок.
[L,XY] = unmesh(E);
Матрица Лапласа определяется как

Lij = {deg (  vi )  , если i = j  −  1   , если    i≠j   и vi    смежны с vj0  ,  в противном случае              

unmesh возвращает матрицу Лапласа L в виде разреженной матрицы.

L
L =

   (1,1)        3
   (2,1)       -1
   (3,1)       -1
   (4,1)       -1
   (1,2)       -1
   (2,2)        2
   (4,2)       -1
   (1,3)       -1
   (3,3)        2
   (4,3)       -1
   (1,4)       -1
   (2,4)       -1
   (3,4)       -1
   (4,4)        3
Видеть L в обычной матричной нотации используйте full команда.
full(L)
ans =

     3    -1    -1    -1
    -1     2     0    -1
    -1     0     2    -1
    -1    -1    -1     3
Матрица координат сетки XY возвращает координаты углов квадрата.
XY
XY =

    -1    -1
    -1     1
     1    -1
     1     1

См. также

|

Документация MATLAB

Поддержка