Можно применить преобразование Box-Cox к любому узлу одноступенчатой или ответной модели элемента (любой модели с глобальным значком), выбрав Модель (Model) > Настроить (Set Up) и введя число лямбды в поле редактирования Box-Cox.
Для гауссовых моделей процессов (GPM) и линейных моделей (полиномов, полиномиальных сплайнов и RBF) можно также использовать диалоговое окно Преобразование бокса-кокса (Box-Cox Transform), описанное в следующем разделе, с помощью кнопки панели инструментов или пункта меню Модель (Model) Преобразование бокса-кокса (Box-Cox Transform).
Возможно, потребуется преобразовать функцию ответа либо для коррекции ненормальности и/или гетероскедастической структуры дисперсии. Полезным классом преобразований для этой цели является преобразование мощности, 
где λ - параметр, подлежащий определению. Бокс и Кокс (1964) показали, как λ и сами коэффициенты регрессии могут быть оценены одновременно с помощью метода максимального правдоподобия. Процедура состоит в проведении стандартной посадки методом наименьших квадратов с использованием
для 
λ
для 
где так называемое геометрическое среднее наблюдений дано
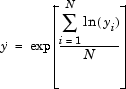
Оценка максимального правдоподобия λ соответствует значению, для которого SSE (λ) из аппроксимированной модели является минимальным. Это значение λ определяется подгонкой модели (предполагается, что она определяется матрицей регрессии для полной модели - X) для различных уровней λ и выбором значения, соответствующего минимальному SSE (λ). График SSE (λ) против λ часто используется для облегчения этого выбора.
Параметр λ сдвигается между диапазонами от -3 до 3 с шагом 0,5.
Можно ввести значение лямбды в поле редактирования, которое приближается к точке на графике с наименьшей МРЗ.
Хотя SSE (λ) является непрерывной функцией λ, рекомендуются простые варианты для λ. Это происходит потому, что практическая разница между 0,5 и 0,593, скажем, вероятно, очень мала, но простое преобразование, такое как 0,5, гораздо легче интерпретировать.
Вы также можете найти приблизительно 100 (1
-) доверительный интервал на l путем вычисления
где - число остаточных степеней свободы, равное (N-q).
В этой формуле λ понимается как значение, которое минимизирует SSE (λ). Следует отметить, что этот доверительный интервал может охватывать более одного инкрементного значения λ. В этом случае любое из этих значений является таким же допустимым, как и любое другое, и можно выбрать любое из этих преобразований для разработки пробных моделей.
Чтобы увидеть эффект различных преобразований, всегда следует смотреть на графики остатков вверху.
Можно создать несколько дочерних узлов одной модели и выбрать различные преобразования для каждого из них, чтобы сравнить их с помощью остальных инструментов браузера модели.
Для ясности рассмотрим следующий пример, который иллюстрирует результаты применения алгоритма Бокса-Кокса к модели полисплайн крутящего момента.
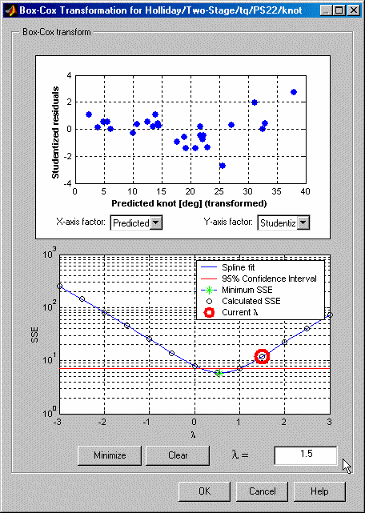
В этом примере минимальное значение SSE (λ) находится вблизи λ = 0. Минимум отмечен зеленым цветом. 95% доверительный предел был рассчитан и нарисован на рисунке в виде красной сплошной линии. В этом примере очевидно, что после округления до ближайшего инкрементного значения, содержащегося в доверительном интервале,
подходит любое λ в диапазоне. Из трех возможных приращений 0, 0,5 и 1 λ = 0,5 является ближайшим к минимальному SSE.
Можно выбрать любую точку на графике, щелкнув значок. Выбранная точка (текущая лямбда) затем выделяется красным цветом. Можно также ввести значения лямбды непосредственно в поле редактирования и нажать Enter.