MUltiple SIgnal Classification (MUSIC) - алгоритм пеленгации высокого разрешения, основанный на разложении собственных значений матрицы ковариации датчика, наблюдаемой в массиве. MUSIC относится к семейству алгоритмов пеленгации на основе подпространства.
Модель сигнала связывает принятые данные датчика с сигналами, излучаемыми источником. Предположим, что существуют D некоррелированных или частично коррелированных источников сигнала sd (t). Данные датчика, xm (t), состоят из сигналов, принятых в матрице, вместе с шумом, нм (t). Снимок данных датчика - это вектор данных датчика, принятый в М элементах массива в один момент t.
[a (
x (t) - вектор M-by-1 принятого снимка данных датчика, которые состоят из сигналов и аддитивного шума.
A является матрицей M-by-D, содержащей векторы поступления. Вектор прихода состоит из относительных фазовых сдвигов в элементах матрицы плоской волны от одного источника. Каждый столбец А представляет вектор поступления из одного из источников и зависит от направления поступления, δ d - направление угла прихода для n-го источника и может представлять либо широкий угол для линейных массивов, либо азимут и угол возвышения для плоских или 3D массивов.
s (t) - вектор D-by-1 значений исходного сигнала от D источников.
n (t) - вектор M-by-1 значений шума датчика.
Важной величиной в любом способе подпространства является сенсорная ковариационная матрица Rx, полученная из принятых данных сигнала. Когда сигналы не коррелируют с шумом, ковариационная матрица датчика имеет две составляющие: ковариационную матрицу сигнала и ковариационную матрицу шума.
+ σn2I
где Rs - исходная ковариационная матрица. Диагональные элементы матрицы ковариации источника представляют мощность источника, а внедиагональные элементы представляют корреляции источника.
ssH}
Для некоррелированных источников или даже частично коррелированных источников Rs является положительно-определённой эрмитовой матрицей и имеет полный ранг D, равный числу источников.
Матрица ковариации сигнала, ARsAH, является матрицей M-by-M, также с рангом D < M.
Предположение алгоритма MUSIC состоит в том, что мощности шума равны для всех датчиков и не коррелируются между датчиками. При этом предположении ковариационная матрица шума становится диагональной матрицей M-на-M с равными значениями вдоль диагонали.
Поскольку истинная матрица ковариации датчика неизвестна, MUSIC оценивает матрицу ковариации датчика, Rx, из матрицы ковариации датчика образца. Ковариационная матрица датчика образца представляет собой среднее из нескольких снимков данных датчика.
) H,
где T - количество снимков файловой системы.
Поскольку ARsAH имеет ранг D, он имеет D положительных действительных собственных значений и M - D нулевых собственных значений. Собственные векторы, соответствующие положительным собственным значениям, охватывают подпространство сигнала, Us = [v1,..., vD]. Собственные векторы, соответствующие нулевым собственным значениям, ортогональны сигнальному пространству и охватывают нулевое подпространство, Un = [uD + 1,..., uN]. Векторы прихода также принадлежат подпространству сигнала, но они являются собственными векторами. Собственные векторы нулевого подпространства ортогональны собственным векторам подпространства сигнала. Собственные векторы нулевого подпространства, ui, удовлетворяют этому уравнению:
=0⇒AHui=0
Следовательно, векторы поступления ортогональны нулевому подпространству.
При добавлении шума собственные векторы ковариационной матрицы датчика с присутствующим шумом являются такими же, как и безшумная ковариационная матрица датчика. Собственные значения увеличиваются на мощность шума. Пусть vi - один из собственных векторов исходного безшумового сигнального пространства. Тогда
+ start02) vi
показывает, что собственные значения сигнального пространства увеличиваются на
Собственные векторы нулевого подпространства также являются собственными векторами Rx. Пусть ui - один из собственных нулевых векторов. Тогда
при собственных значениях, не равных нулю,, а (в случае, если они не равны нулю). Нулевое подпространство становится шумовым подпространством.
MUSIC работает путем поиска всех векторов поступления, которые ортогональны подпространству шума. Для выполнения поиска MUSIC создает зависящее от угла прихода выражение мощности, называемое псевдоспектром MUSIC:
UnUnHa (ϕ→)
Когда вектор прихода ортогональен шумовому подпространству, пики псевдоспектра бесконечны. На практике, поскольку существует шум и поскольку истинная ковариационная матрица оценивается дискретизированной ковариационной матрицей, векторы прихода никогда не являются точно ортогональными к подпространству шума. Затем углы, при которых PMUSIC имеет конечные пики, являются требуемыми направлениями прихода. Поскольку псевдоспектр может иметь больше пиков, чем есть источники, алгоритм требует, чтобы в качестве параметра было указано количество источников D. Затем алгоритм выбирает наибольшие пики D. Для однородного линейного массива (ULA) пространство поиска представляет собой одномерную сетку из широкополосных углов. Для плоских и 3D массивов пространство поиска представляет собой двумерную сетку углов азимута и отметки.
Для ULA знаменателем в псевдоспектруме является многочлен в , но также может считаться многочленом в комплексной плоскости. В этом случае можно использовать методы поиска корней для решения корней, zi. Эти корни не обязательно лежат на единичном круге. Однако Root-MUSIC предполагает, что корни D, ближайшие к единичной окружности, соответствуют истинным направлениям источника. Затем можно вычислить направления источника из фазы комплексных корней.
Когда некоторые из сигналов источника D коррелированы, Rs является дефицитным по рангу, что означает, что он имеет меньше, чем D ненулевых собственных значений. Следовательно, число нулевых собственных значений ARsAH превышает число M-D нулевых собственных значений для несоотнесенного исходного случая. Производительность MUSIC ухудшается, когда сигналы коррелируются, как это происходит в среде многолучевого распространения. Способ компенсации корреляции заключается в использовании пространственного сглаживания.
Пространственное сглаживание использует свойства преобразования однородного массива. Рассмотрим два коррелированных сигнала, поступающих в L-элемент ULA. Исходная ковариационная матрица, Rs - сингулярная матрица 2 на 2. Матрица вектора поступления является матрицей L-by-2
(ф.1) | a (ф2)]
для сигналов, поступающих с широкополосных углов ф.1 и ф2. Величина k является числом сигнальных волн. a (start) представляет вектор прихода под углом
Второй массив можно создать путем перемещения первого массива вдоль его оси на одно расстояние элемента d. Матрица поступления для второго массива:
где векторы поступления равны исходным векторам поступления, но умножены на фазовый сдвиг, зависящий от направления. При переводе исходного массива J -1 еще раз получаются J-копии массива. Если из всех этих копий сформировать один массив, то длина одного массива будет M = L + (J - 1).
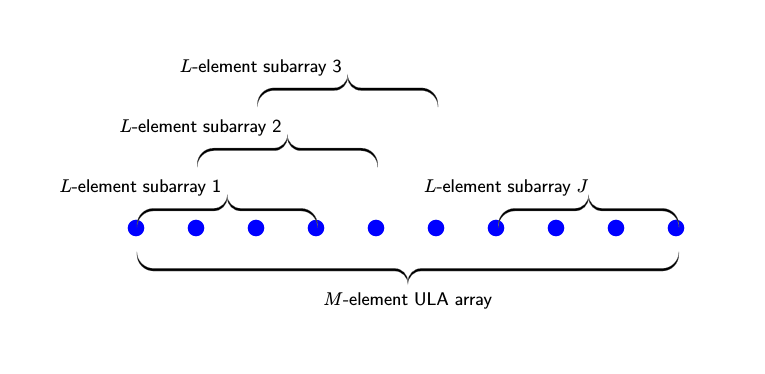
На практике начинается с массива M-элементов и формируются перекрывающиеся J-массивы. Число элементов в каждом подматрице равно L = M - J + 1. На следующем рисунке показана взаимосвязь между общей длиной массива, M, количеством подрешеток, J, и длиной каждого подрешетки, L.
Для подрешетки pth матрицей поступления исходного сигнала является
A1Pp − 1P = [eikdcosф100eikdcc
Исходная матрица вектора прихода постмультиплексируется диагональной фазовой матрицей.
Последним шагом является усреднение ковариационных матриц сигнала по всем J-субчипам для формирования ковариационной матрицы усредненного сигнала, Ravgs. Средняя сигнальная ковариационная матрица зависит от сглаженной исходной ковариационной матрицы, Rsmooth.
(Pp − 1) H.
Можно показать, что диагональные элементы сглаженной исходной ковариационной матрицы совпадают с диагональными элементами исходной исходной ковариационной матрицы.
niH=1J∑p=1JRs= (Rs) ii
Однако не диагональные элементы уменьшены. Коэффициент уменьшения представляет собой диаграмму направленности матрицы J-элементов.
cosoft1 − cosoft2)) (Rs) ij
Таким образом, можно уменьшить деградирующий эффект корреляции источников, формируя субчипы и используя сглаженную ковариационную матрицу в качестве входных данных алгоритма MUSIC. Из-за диаграммы направленности большее угловое разделение источников приводит к уменьшению корреляции.
Пространственное сглаживание для линейных массивов легко распространяется на 2D и 3D однородные массивы.