Двухлучевой канал распространения является следующим шагом в усложнении от канала свободного пространства и является простейшим случаем многолучевого распространения среды. Канал свободного пространства моделирует траекторию прямой линии визирования от точки 1 до точки 2. В двухлучевом канале среда задана как однородная, изотропная среда с отражающей планарной границей. Граница всегда устанавливается равной z = 0. Существует не более двух лучей, распространяющихся от точки 1 к точке 2. Первый путь луча распространяется вдоль той же линии визирования, что и в канале свободного пространства (см. phased.FreeSpace Системный object™). Траектория линии визирования часто называется прямой траекторией. Второй луч отражается от границы перед распространением на точку 2. Согласно Закону отражения, угол отражения равен углу падения. При моделировании на малых расстояниях, таких как сотовые системы связи и автомобильные радары, можно предположить, что отражающая поверхность, поверхность земли или океана, является плоской.
На рисунке показаны два пути распространения. Из положения источника, ss и положения приемника, sr, можно вычислить углы прихода обоих путей, θ′los и θ′rp. Углы прихода - это углы возвышения и азимута прибывающего излучения относительно локальной системы координат. В этом случае локальная система координат совпадает с глобальной системой координат. Вы также можете вычислить углы передачи, В глобальных координатах угол отражения на границе тот же, что и углы startrp и θ′rp. Угол отражения важно знать при использовании зависимых от угла данных потери отражения. Угол отражения можно определить с помощью rangeangle и установка опорных осей в глобальную систему координат. Общая длина траектории для линии визирования показана на рисунке Rlos, которая равна геометрическому расстоянию между источником и приемником. Общая длина пути для отраженного пути равна Rrp = R1 + R2. Величина L - это диапазон земли между источником и приемником.
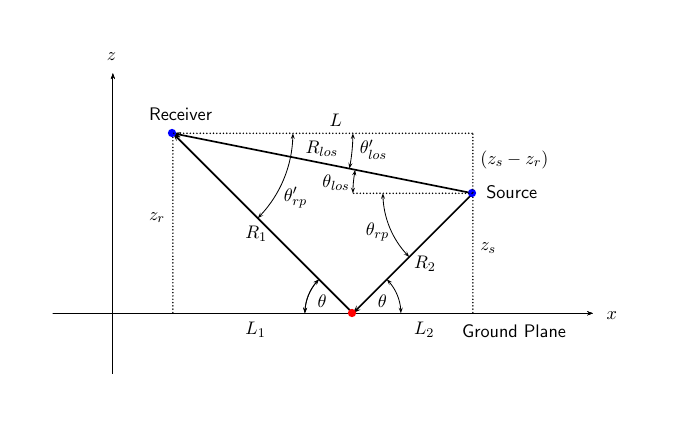
В глобальной системе координат можно легко получить точные формулы для длин и углов траектории с точки зрения диапазона земли и высоты объекта.
− zr) Ltanstartrp = − (zs + zr) Lθ′los=−θlosθ′rp=θrp