Газовая сторона теплообменника
Simscape / Жидкости / Жидкие Сетевые интерфейсы / Теплообменники / Фундаментальные Компоненты
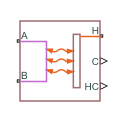
Блок интерфейса теплообменника (G) моделирует теплопередачу газовым потоком внутри теплообменника. Используйте второй блок теплообменника для моделирования пары жидкостей. Границы раздела могут находиться в различных областях текучей среды, таких как один в жидкости и один в газе. Используйте блок теплопередачи E-NTU для соединения интерфейсов и улавливания теплообмена между текучими средами.
Конструкция блока с фиксированным объёмом позволяет улавливать изменения массового расхода жидкости за счёт сжимаемости. Общая скорость накопления массы равна сумме массовых скоростей потока через порты:
где - массовый расход, а - массовый расход. Нижние индексы обозначают порты A и B. Массовый расход является положительным, когда он направлен в газовый канал. Изменения плотности отражаются на скорости накопления массы:
pdudt] V,
где:
start- плотность.
p - давление.
u - удельная внутренняя энергия.
V - объем.
Уравновешивание импульса между входным и выходным отверстиями теплообменника определяет направление потока и скорость внутри теплообменника. Изменения импульса обусловлены в первую очередь потерями трения от поворотов труб, которые переходят в изменения давления. Локальные сопротивления, такие как изгибы, колена и тройники, могут приводить к разделению потока, что приводит к незначительным дополнительным потерям давления. Для постоянных потоков массовый расход остается постоянным.
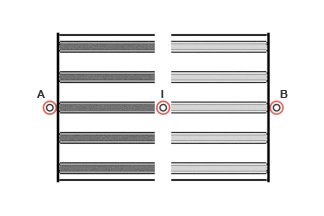
Баланс импульса прикладывается к каждому сегменту объема газа (трубы). На этом рисунке показан банк труб, разделенный на два объема и три узла. Узлы соответствуют портам A, B и объему текучей среды. I. Состояния текучей среды, такие как давление и температура, и свойства текучей среды, такие как плотность и вязкость, определяются в этих узлах.
Следует отметить, что инерция потока незначительна, и поток считается квазистационарным. Перемещение переходных процессов к массовым расходам может быть смещено: из-за связи между плотностью, давлением и температурой распространение изменений по всей системе не является мгновенным. Другие источники и поглотители импульса, такие как различия в головке между окнами или радиальные деформации стенки канала, не рассматриваются. Баланс импульса для половины объема в порту A:
Δpf, A,
где p - давление в узле, указанном в подстрочном индексе. Δpf, A - общая потеря давления между портовым узлом и внутренним узлом из-за трения. Общая потеря давления включает в себя как большие, так и незначительные потери. Для половины объема в порту B баланс импульса равен:
Δpf, B.
Изменения давления вследствие трения изменяются с квадратом массового расхода для турбулентных потоков и с величиной массового расхода для ламинарных потоков. Это изменение давления характеризуется тремя безразмерными параметрами: коэффициентом трения Дарси, коэффициентом потери давления и числом Эйлера. Эти числа вычисляются на основе эмпирических корреляций или оцениваются на основе таблиц поиска в зависимости от параметра параметризации потери давления.
Классификация «ламинарного» или «турбулентного» потока основана на числе Рейнольдса. Когда число Рейнольдса выше параметра ограничения нижнего числа Рейнольдса турбулентного потока, поток становится полностью турбулентным. Ниже параметра верхнего предела числа Рейнольдса потока Ламинара поток является полностью ламинарным. Числа Рейнольдса между этими значениями указывают на переходный поток. Переходные потоки имеют характеристики как ламинарных, так и турбулентных потоков. В языке Simscape™ Fluids™ между этими ограничивающими значениями применяется численное смешение.
Correlations for tubesДля трубок используется коэффициент трения Дарси, fD. В половинном объеме порта A баланс импульса составляет:
LAdd2),
где L - длина трубки, а LAdd - добавленная длина трубки, которая воспроизводит незначительные потери вязкости, если используется вместо колен, тройников, штуцеров или других локальных сопротивлений. А - площадь поперечного сечения трубы; в случае неравномерной площади поперечного сечения следует использовать амин. DH - гидравлический диаметр трубы или диаметр окружности, равный по площади поперечному сечению трубы:
4AMinπ.
Если труба имеет круглое поперечное сечение, гидравлический диаметр и диаметр трубы одинаковы.
Для половины объема в порту B баланс импульса равен:
LAdd2).
Для турбулентных потоков коэффициент трения Дарси рассчитывается с корреляцией Хааланда. Номер Рейнольдса устанавливается в ограничивающем порту:
1,11]} -2,
где αR - шероховатость стенки, принимаемая за характерную высоту. Этот параметр задается в параметре абсолютная шероховатость внутренней поверхности.
Для ламинарных потоков коэффициент трения зависит от формы трубы и рассчитывается с учетом коэффициента формы трубы:
λ Re,
где λ - коэффициент формы. Число Рейнольдса вычисляется в ограничивающем порте следующим образом:
Подставляя Re в уравнение потерь давления в порту A, баланс импульса преобразуется в:
LAdd2),
Аналогично, для половины объема в порту B баланс импульса равен:
LAdd2).
Для каналов, отличных от трубок, следует использовать коэффициент потери давления Для турбулентных потоков в половине объема в порту A баланс импульса составляет:
Для турбулентных потоков в половине объема в порту B баланс импульса составляет:
Для ламинарных потоков в половине объема в порту A баланс импульса составляет:
где ReL - параметр верхнего предела числа Рейнольдса потока Ламинара. Для ламинарных потоков в половине объема в порту B баланс импульса составляет:
Tabulated data - Darcy friction factor vs. Reynolds numberМожно использовать табличные данные для определения коэффициента трения Дарси на основе числа Рейнольдса для потоков труб. Для половины объема на порте A баланс импульса:
LAdd2).
Для половины объема в порту B баланс импульса равен:
LAdd2).
Для турбулентного режима коэффициент трения определяется из табличной функции числа Рейнольдса:
Re).
Точки останова табличной функции получаются из параметров векторного блока. Вектор числа Рейнольдса для параметра коэффициента трения Дарси определяет независимую переменную, а параметр вектора коэффициента трения Дарси определяет зависимую переменную. Между точками останова применяется линейная интерполяция. За пределами табличного диапазона данных коэффициент трения определяется ближайшей точкой останова.
В ламинарном режиме коэффициент трения рассчитывается из коэффициента формы λ:
λ Re.
Tabulated data - Euler number vs. Reynolds numberДля определения номера Эйлера на основе номера Рейнольдса можно использовать табличные данные. Этот расчет зависит от режима потока, и число Эйлера формулируется как табличная функция числа Рейнольдса:
Re).
Точки останова в Tabulated data - Euler number vs. Reynolds number определяются векторами числа Рейнольдса и числа Эйлера. Вектор числа Рейнольдса для параметра числа Эйлера определяет независимые переменные, числа Рейнольдса и параметр вектора числа Эйлера определяет зависимую переменную, число Эйлера, для каждого числа Рейнольдса. Линейная интерполяция используется для определения значений между точками останова. За пределами табличного диапазона данных используется значение в ближайшей точке останова.
Для турбулентных потоков баланс импульса для половины объема в порту A составляет:
где Eu - число Эйлера в порту A. Для турбулентных потоков баланс импульса для половины объема в порту B составляет:
Для ламинарного потока в половине объема в порту A баланс импульса составляет:
где ReL - верхний параметр ограничения числа Рейнольдса потока Ламинара, а EuL - число Эйлера, вычисленное из табулированных данных с этим числом Рейнольдса. Для ламинарного потока в половине объема в порту B баланс импульса равен:
Энергетический баланс в объеме газа представляет собой сумму его скоростей потока через границы каналов и связанного с этим теплопередачи. Энергия может передаваться путем продвижения в портах и конвекции в стенке. Хотя проводимость способствует энергетическому балансу в портах, она часто ничтожно мала по сравнению с адвекцией. Однако проводимость не пренебрежимо мала в почти стационарных текучих средах, например, когда текучие среды находятся в застойном состоянии или меняют направление. Уравнение энергетического баланса:
где:
- частная производная внутренней энергии объема газа по отношению к давлению при постоянной температуре и объеме.
pI - давление объема газа.
- частная производная внутренней энергии объема газа по отношению к температуре при постоянном давлении и объеме.
TI - температура объема газа.
ФА и ФВ - расход энергии в портах А и В соответственно.
Q - скорость теплопередачи.
Адвекция и проводимость учитываются в Λ, а конвекция - в Q. Скорость теплопередачи положительна при направлении в объем газа.
Теплопередача между двумя текучими средами теплообменника происходит множеством способов: через конвекцию на границах раздела текучих сред, проводимость через слои наплавленного загрязнения и проводимость через толщину стенки.
Теплопередача выходит за пределы газового канала и поэтому требует других блоков для моделирования всей системы теплообменника. Второй блок сопряжения теплообменника моделирует второй канал потока, в то время как блок теплопередачи E-NTU моделирует поток тепла через стенку. Параметры теплопередачи, относящиеся к газовому каналу, но требуемые блоком теплопередачи E-NTU, доступны через физические сигнальные порты:
Порт C выводит скорость теплопроизводительности, которая является мерой способности газа поглощать тепло и требуется для расчета количества блоков теплопередачи (NTU). Коэффициент теплоемкости рассчитывается как:
где CR - скорость теплопроизводительности, а cp - удельная теплота.
Порт HC выдает коэффициент теплопередачи, U.
Если коэффициент теплопередачи обрабатывается как константа, его значение является равномерным по каналу потока. Если коэффициент теплопередачи является переменным, он рассчитывается на каждом порту из выражения:
Q,
где Nu - число Нуссельта, k - теплопроводность, а DH, Q - гидравлический диаметр для теплопередачи. Гидравлический diameterDH, Q вычислен как:
4AMinLQSQ,
где QQ - параметр площади поверхности теплопередачи, а LQ - длина пути потока для параметра теплопередачи.
Нижней границей среднего коэффициента теплопередачи является параметр Минимальный коэффициент теплопередачи газ-стенка.
Число Нуссельта получено из эмпирических корреляций с числами Рейнольдса и Прандтля. Используйте параметр параметризации теплопередачи, чтобы выбрать наиболее подходящую формулировку для моделирования.
Простейшая параметризация, Constant heat transfer coefficientполучают коэффициент теплопередачи непосредственно из значения параметра коэффициента теплопередачи газ-стенка. Correlations for tubes использует аналитические выражения с постоянными или вычисленными параметрами для фиксации зависимости числа Нуссельта от режима расхода для трубных потоков.
Остальные параметризации являются табличными функциями числа Рейнольдса. Они полезны для изменения чисел Нуссельта или коэффициентов теплопередачи в режимах потока. Функции генерируются из экспериментальных данных, связывающих число Рейнольдса с фактором Колберна или числа Рейнольдса и Прандтля с числом Нуссельта.
Constant heat transfer coefficientИспользуя Constant heat transfer coefficient, указанный в параметре Коэффициент теплопередачи газ-стенка, устанавливает коэффициент теплопередачи как постоянный и не использует в расчетах число Нуссельта. Используйте эту параметризацию как простую аппроксимацию для газовых потоков, ограниченных ламинарным режимом.
Correlation for tubesЧисло Нуссельта зависит от режима потока при использовании Correlation for tubes. Для турбулентных потоков его значение изменяется пропорционально числу Рейнольдса и рассчитывается по корреляции Гниелинского:
(Pr2/3 − 1),
где Re - число Рейнольдса, Nu - число Нуссельта, а Pr - число Прандтля. Коэффициент трения f аналогичен коэффициенту, используемому при расчетах потерь давления в трубах. Для ламинарных потоков число Нуссельта является константой. Его значение получается из числа Нуссельта для параметра теплопередачи ламинарного потока, NuL:
NuL.
Tabulated data - Colburn factor vs. Reynolds numberДля определения коэффициента Колберна на основе числа Рейнольдса можно использовать табличные данные. Уравнение Колберна используется для определения числа Нуссельта, которое изменяется пропорционально числу Рейнольдса. J-фактор Колберна - мера пропорциональности между числами Рейнольдса, Прандтля и Нуссельта:
ReQPr1/3.
ReQ - число Рейнольдса, основанное на гидравлическом диаметре для теплопередачи, DH, Q, и от минимальной площади свободного потока канала, AMin:
Tabulated data - Nusselt number vs. Reynolds number & Prandtl numberДля определения числа Нуссельта из чисел Прандтля и Рейнольдса можно использовать табличную функцию. Линейная интерполяция используется для определения значений между точками останова. Число Нуссельта является функцией как Re, так и Pr, и поэтому числовой вектор Рейнольдса для числа Нуссельта, числовой вектор Прандтля для числа Нуссельта и числовая таблица Нуссельта, параметры Nu (Re, Pr) определяют точки останова таблицы:
Pr).
Число Рейнольдса в таблице должно рассчитываться с использованием гидравлического диаметра для теплопередачи, DH, Q.