Общее сопротивление в двухфазной ветви флюида
Библиотека Simscape/Foundation/Двухфазная жидкость/Элементы
Блок сопротивления потоку (2P) моделирует общее падение давления в двухфазной ветви сети текучей среды. Перепад давления пропорционален квадрату массового расхода и плотности двухфазной текучей среды. Константа пропорциональности определяется по номинальному рабочему условию, заданному в диалоговом окне блока.
Этот блок используется, когда единственными данными, доступными для компонента, является перепад давления в зависимости от массового расхода. Объедините блок с другими, чтобы создать пользовательский компонент, который более точно фиксирует падение давления, которое он вызывает - например, теплообменник на основе блока камеры.
Предполагается, что объем жидкости внутри сопротивления потоку является незначительным. Массовый расход через один порт должен быть точно равен массовому расходу через другой порт:
где и определяются как массовые расходы в компонент через порты А и В соответственно.
Энергия может входить и выходить из сопротивления потока только через двухфазные отверстия для текучей среды. Теплообмен между стеной и окружающей средой не происходит. Кроме того, никакой работы над жидкостью или с ее помощью не выполняется. Расход энергии через один порт должен быть точно равен расходу энергии через другой порт:
= 0,
где A и B - скорости потока энергии в сопротивление потока через порты A и B.
Соответствующие внешние силы на текучую среду включают в себя силы, вызванные давлением в окнах, и силы, обусловленные вязким трением на стенках компонента. Гравитация игнорируется, как и другие силы тела. Выражение фрикционных сил в терминах коэффициента потерь, дает полуэмпирическое выражение:
где:
Δp - перепад давления от порта A к порту B, то есть pA + pB.
λ - коэффициент потерь.
ν определенный объем, инверсия массовой плотности ρ - то есть, 1/ρ.
S - площадь потока.
Уравнение перепада давления реализуется с двумя модификациями. Во-первых, чтобы обеспечить возможность изменения знака при изменении направления потока, его переписывают:
где перепад давления является положительным, только если массовый расход слишком велик. Во-вторых, чтобы исключить сингулярности из-за обращения потока - сингулярности, которые могут представлять проблему для численных решателей во время моделирования - он линеаризуется в небольшой области околонулевого потока:
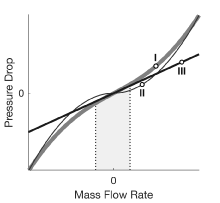
где - пороговый массовый расход, ниже которого происходит линеаризация перепада давления. На рисунке показан измененный перепад давления относительно локального массового расхода (кривая I):
Выше падение давления приближается к тому, которое выражено в исходном уравнении (кривая II), и оно изменяется в зависимости от . Эта зависимость соизмерима с зависимостью, наблюдаемой в турбулентных потоках.
Ниже падение давления приближается к прямой линии с уклоном, частично зависящим от (кривая III), и изменяется с . Эта зависимость соизмерима с зависимостью, наблюдаемой в ламинарных потоках.
Для простоты моделирования в качестве блочного параметра не требуется коэффициент потерь. Вместо этого он автоматически вычисляется по номинальному условию, заданному в диалоговом окне блока:
где звездочка (*) обозначает значение в номинальном рабочем состоянии. Все эти расчеты основаны на предположении, что пороговый массовый расход намного меньше номинального значения *. Заменяя фракцию (2S2) в выражении для падения давления, получают:
).
или, эквивалентно:
где C - постоянная пропорциональность между падением давления через сопротивление потоку и локальным массовым расходом. Он определяется как:
Если предполагается, что удельный объем и, следовательно, плотность массы инвариантны, то его номинальные и фактические значения всегда должны быть равны. Это происходит всякий раз, когда номинальное значение указано в диалоговом окне блока как0- специальное значение, используемое для сигнализации блоку о том, что определенный объем является константой. Соотношение этих двух равно 1 и продукт C, уменьшенный до: