Номинальные значения позволяют задать ожидаемую величину переменной в модели аналогично заданию номинального значения трансформатора или заданию диапазона на вольтметре. В этом примере показано, как можно точно настроить масштабирование отдельных переменных в модели для повышения производительности решателя и надежности моделирования.
Когда решатель выполняет численное моделирование и анализ, он использует переменные без единиц измерения. Номинальные значения - это способ преобразования технических переменных с единицами измерения в переменные без единиц измерения и их масштабирования для оптимальной производительности решателя. Номинальное значение имеет значение с единицей измерения, и эта единица измерения используется для удаления единицы измерения для числовых вычислений. Затем номинальное значение определяет величину переменной, как видно из числовых алгоритмов. Обычно полезно иметь величины аналогичного масштаба.
Рассмотрим простую модель масса-пружина-демпфер с большой постоянной пружины.
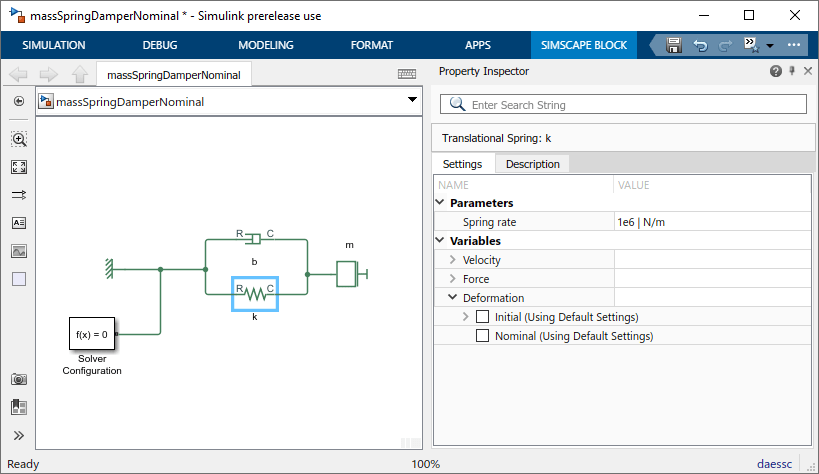
Модель использует настройки параметров блока по умолчанию, за исключением скорости пружины:
Скорость пружины, k = 1e6 Н/м
Коэффициент демпфирования, b = 100 Н/( м/с)
Масса, м = 1 кг
Начальная переменная массовой скорости, v, имеет High приоритет и исходное целевое значение 0,1 м/с. Модель использует номинальные значения по умолчанию с m в качестве единицы измерения длины.
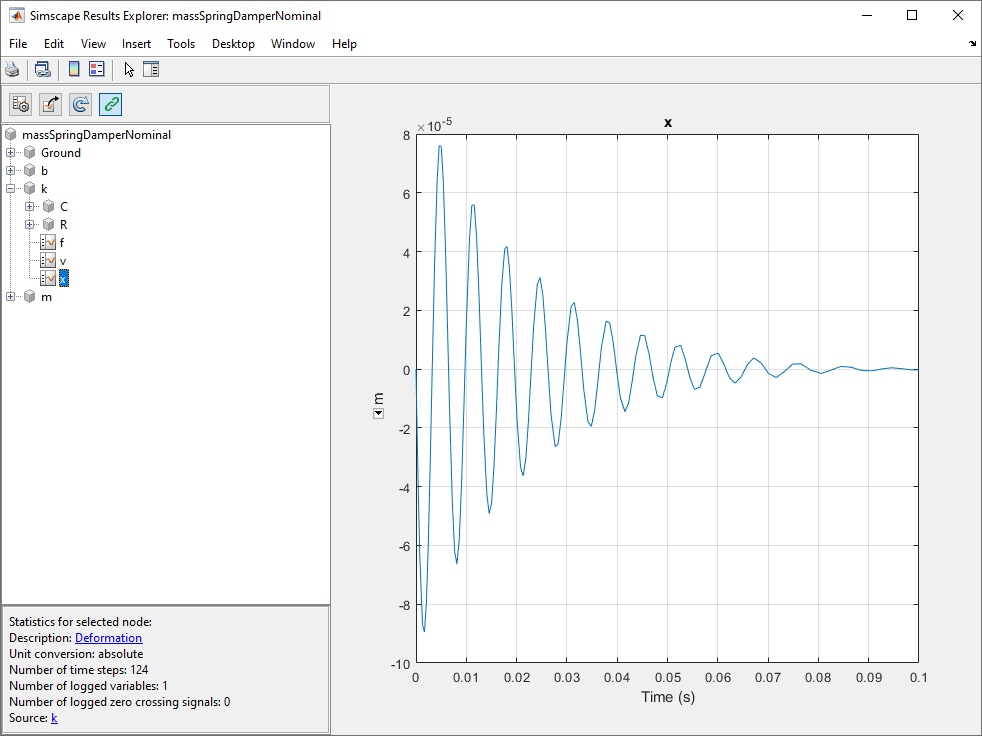
При моделировании этой модели переменная деформации (положения) пружины x мала в диапазоне 10 ^ -5 м.
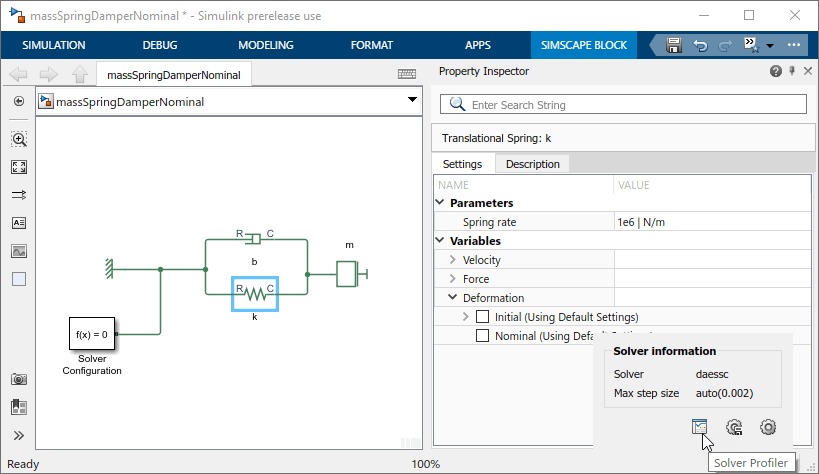
Откройте профилировщик решателя, щелкнув гиперссылку в правом нижнем углу окна модели.
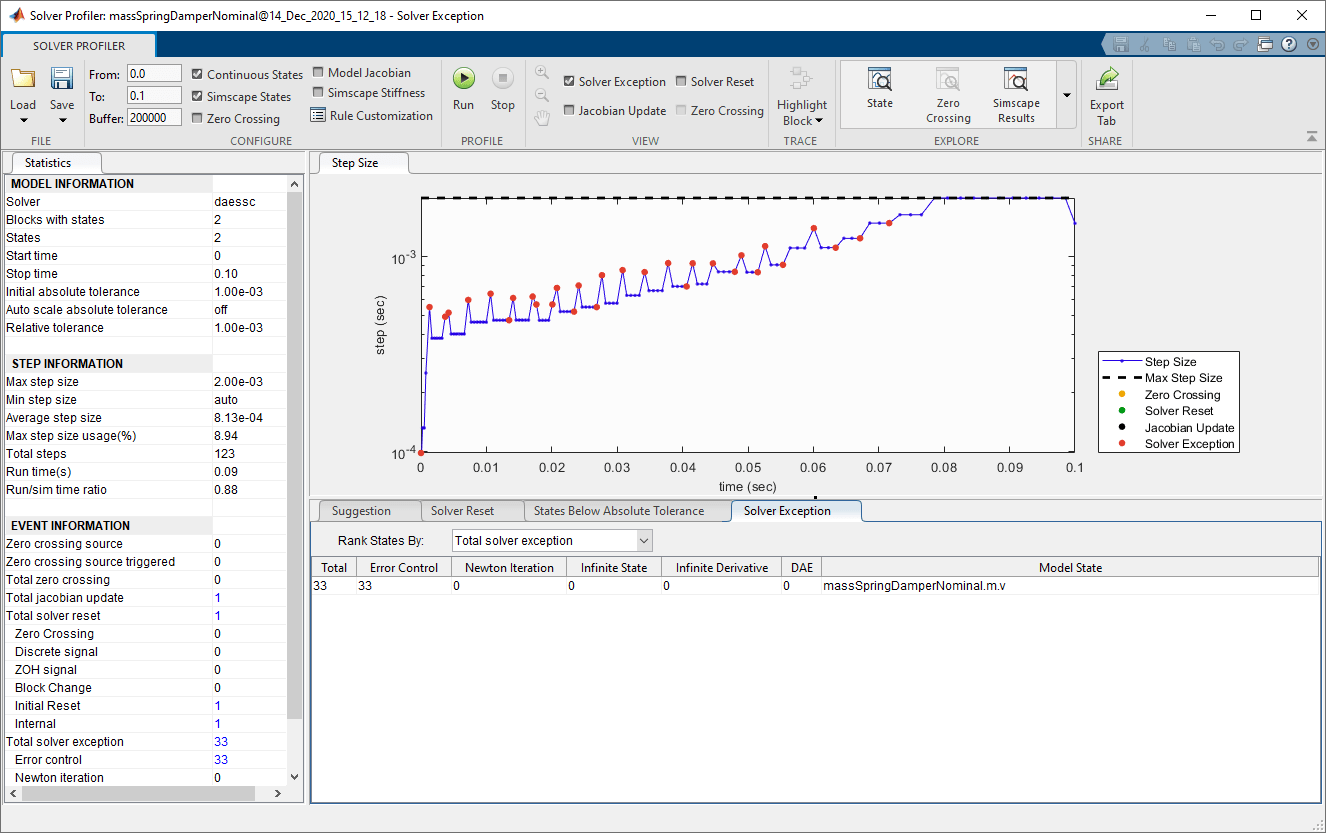
Решатель полностью игнорирует переменную положения и просто смотрит на переменную скорости. Численная величина положения ниже допуска для этой переменной.
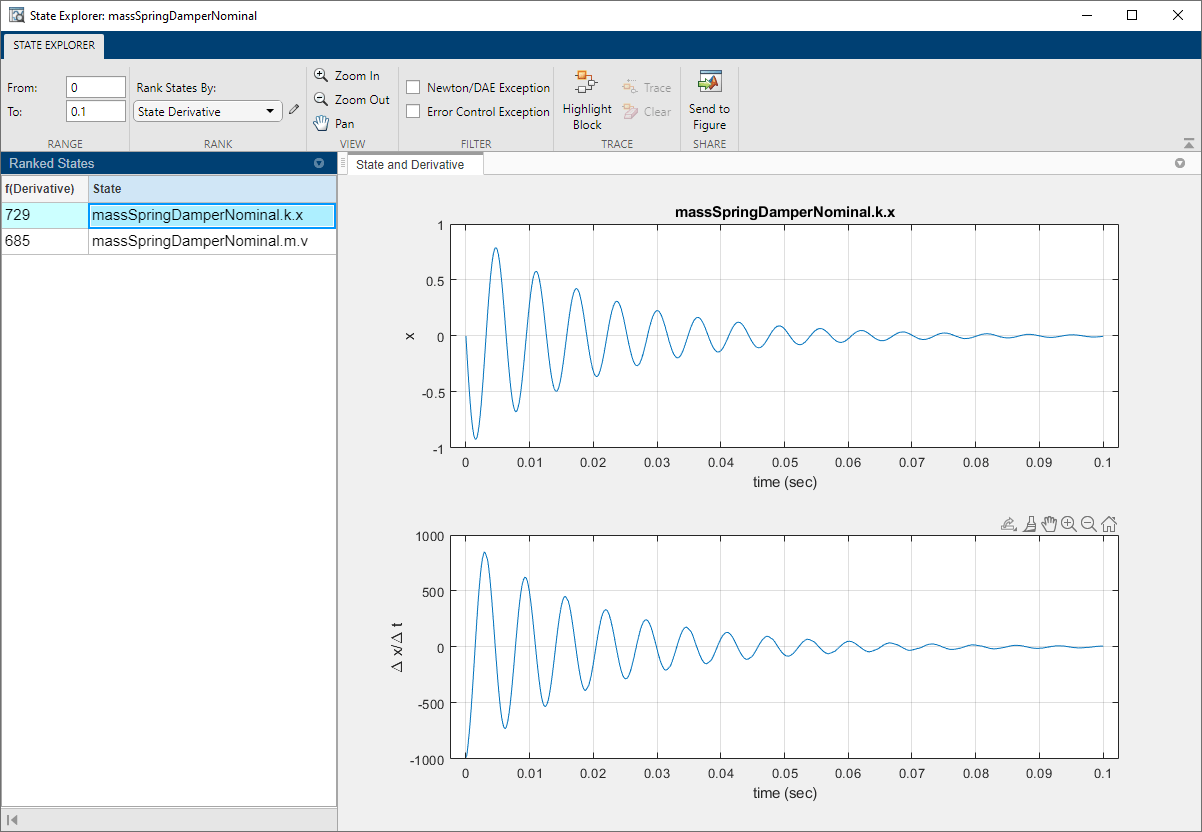
Средство просмотра состояний, доступное из панели инструментов профилировщика решателя, показывает величину каждой переменной, видимую решателями.
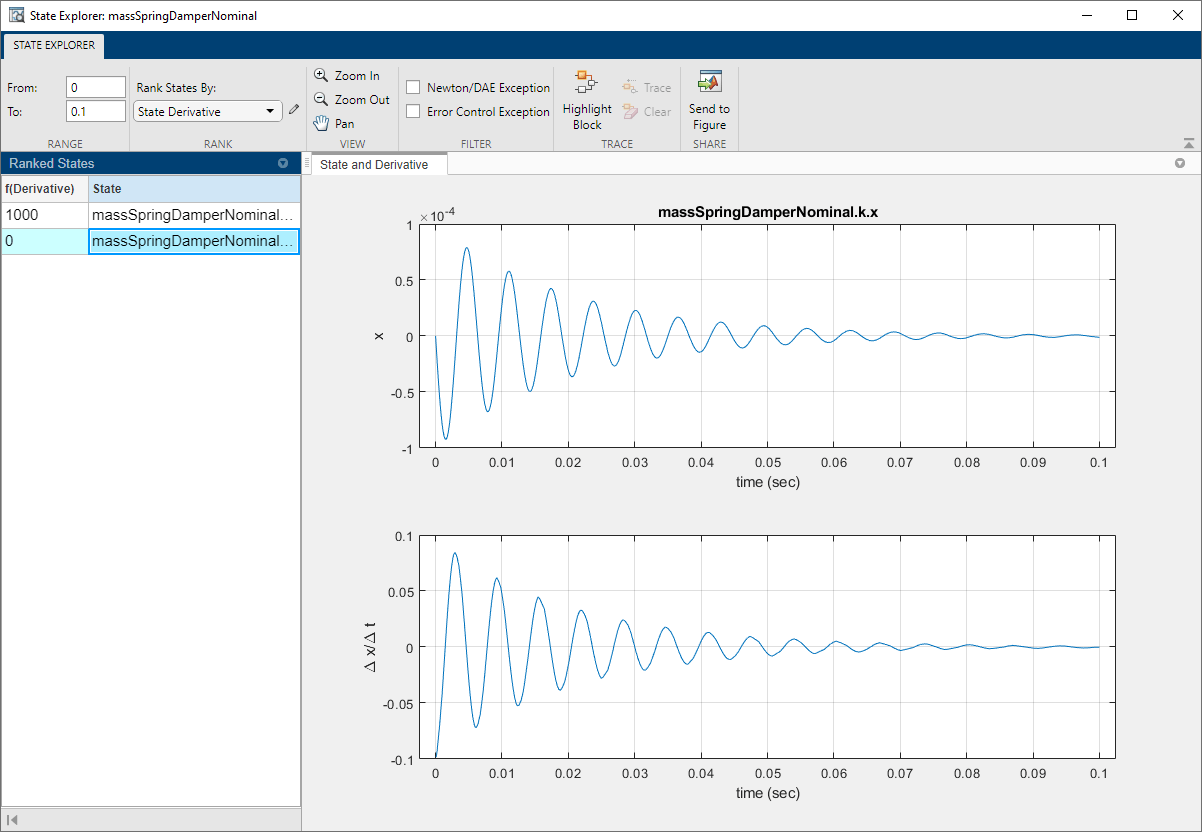
Ситуация ясна, если взглянуть на уравнения модели:
Когда k очень велик, по сравнению с m и b, то x мал, так что произведение k * x имеет приемлемый размер, по сравнению с другими членами в уравнении. Чтобы исправить ситуацию, нам нужно масштабировать x. Другими словами, мы должны выбрать номинальное значение для x, которое мало, так что масштабированная переменная, xs, становится более разумным размером:
где c - большой. Например, если номинальное значение равно 1 мкм, а исходное значение x равно m, то c равно 1e6. Затем уравнения становятся:
⋅xs=0dxsdt=c⋅v
и термины имеют величины одинакового масштаба.
Применим этот принцип масштабирования к переменным модели. Сначала используйте инспектор свойств для изменения номинального значения переменной деформации пружины, x, на 100 um (1е-4 м).
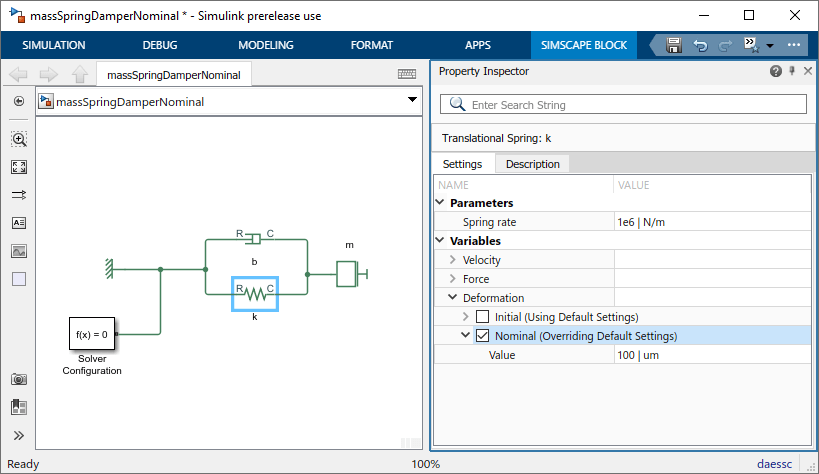
Аналогично, измените номинальное значение переменной Velocity массы на 10 см/с (0,1 м/с).
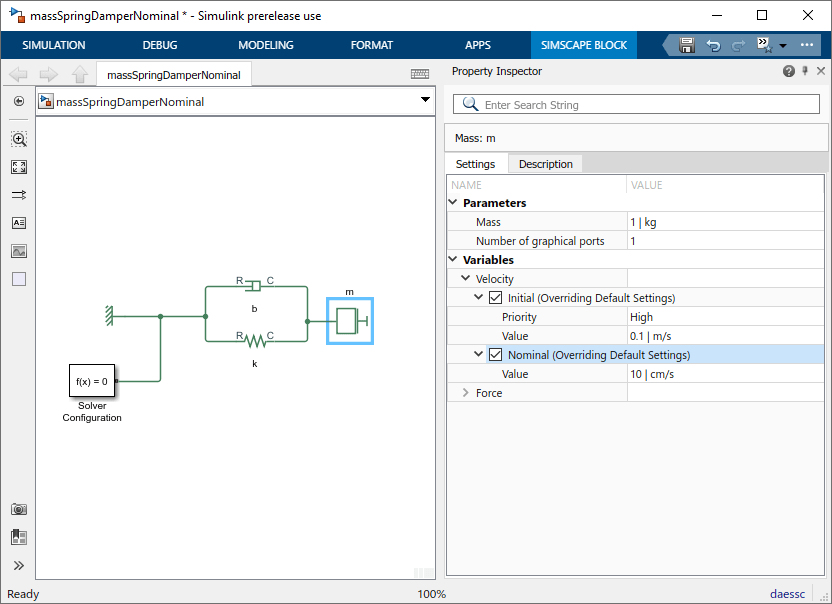
Это приводит масштаб величины обеих переменных, видимых решателем, приблизительно к 1.
Повторно запустите моделирование.
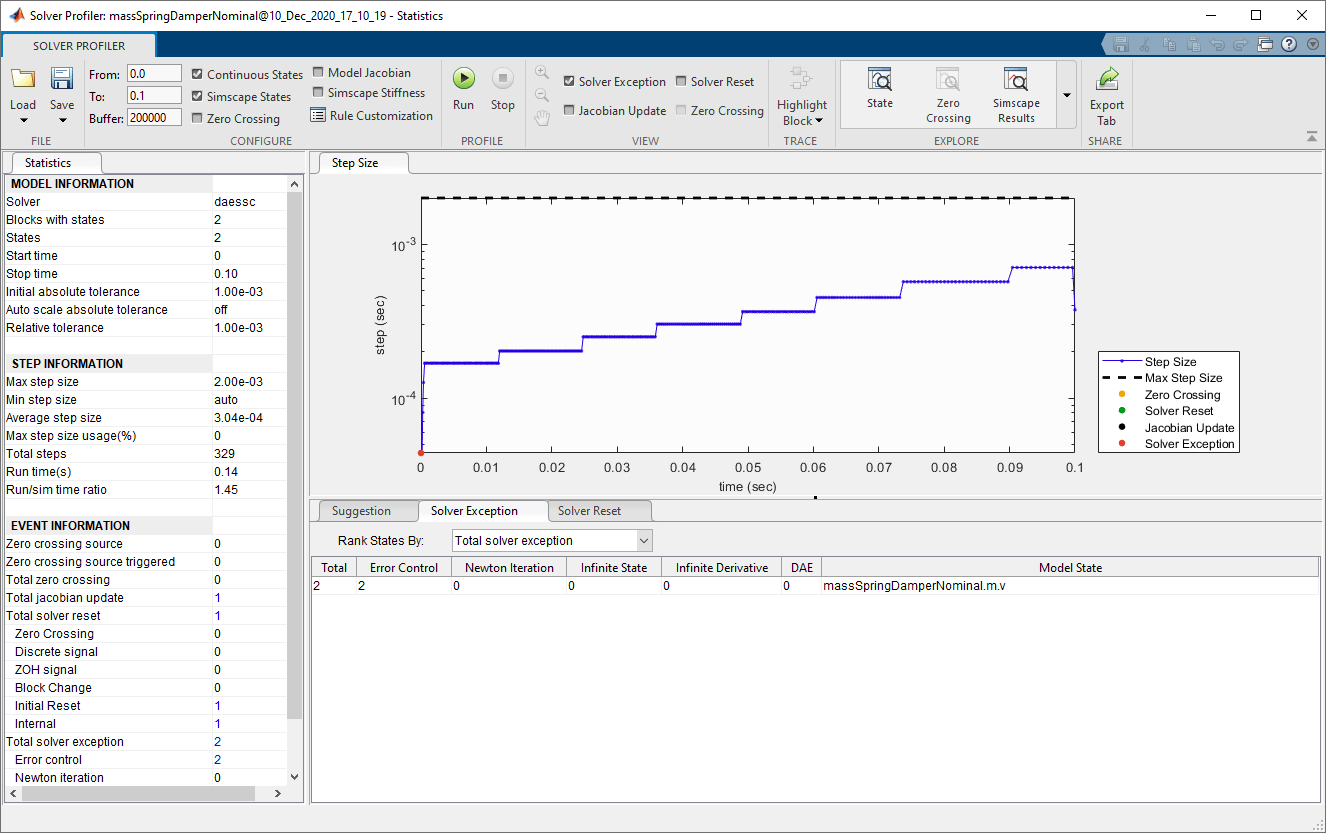
В начале моделирования существует только два исключения решателя.
Заметим, что эффективный абсолютный допуск теперь жестче для массовой скорости. Эффективный абсолютный допуск для Simscape™ моделей имеет единицу измерения и рассчитывается как (номинальное значение * глобальное AbsTol без единиц). В первом прогоне моделирования эффективный абсолютный допуск составлял 1e-3 м/с, а теперь он равен 1e-4 м/с, потому что номинальное значение изменило величину и глобальное AbsTol по-прежнему 1e-3. Однако скорость моделирования аналогична, даже при увеличенной AbsTol по скорости масс и увеличенным шагам времени.
Значения, видимые решателем, одинаковы по величине как для переменных скорости, так и для переменных положения.
Теперь измените глобальный AbsTol кому 1e-2, чтобы более точно соответствовать точности переменной скорости во время первого прогона моделирования.
Повторно запустите моделирование.
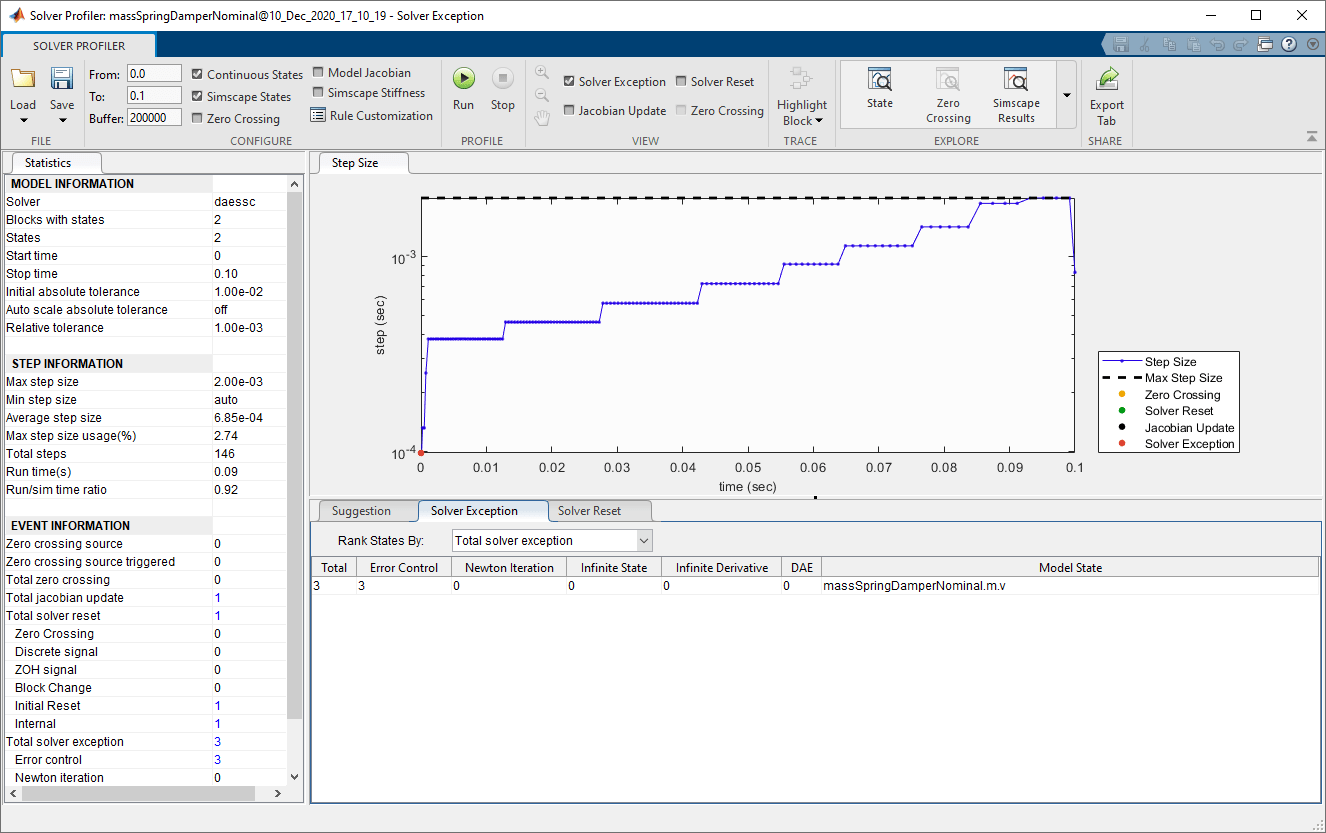
Временные интервалы аналогичны, и количество исключений равно 3, также в начале моделирования.