Альфа-бета-ноль до dq0, dq0 до альфа-бета-ноль

Выполнить преобразование из стационарной системы отсчета αβ0 во вращающуюся систему отсчета dq0 или обратную

Библиотека

Simscape / Электрический / Специализированные Энергосистемы / Контроль

Описание

Блок Alpha-Beta-Zero to dq0 выполняет преобразование компонентов αβ0 Clarke в фиксированной системе координат в компоненты dq0 Park во вращающейся системе координат.

Блок от dq0 до Alpha-Beta-Zero выполняет преобразование компонентов dq0 Park во вращающейся опорной системе координат в компоненты αβ0 Clarke в фиксированной опорной системе координат.

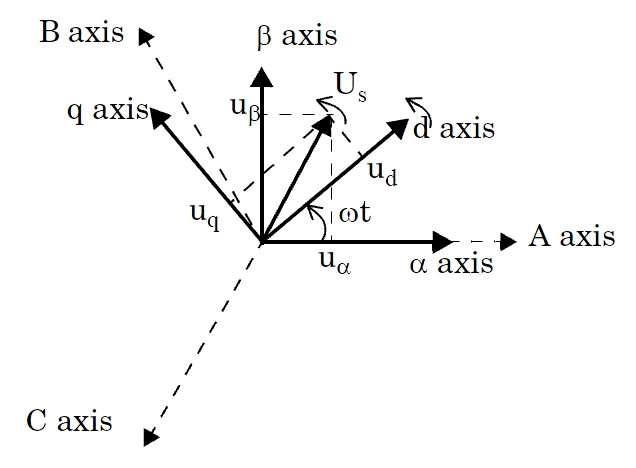
Блок поддерживает два условных обозначения, используемых в литературе для преобразования парка:

Вращающаяся рама выровнена по оси A при t = 0. Этот тип преобразования Парка также известен как преобразование Парка на основе косинуса.
Вращающаяся рама выровнена на 90 градусов позади оси A. Этот тип преобразования Парка также известен как преобразование Парка на основе синуса. Используйте его в моделях Simscape™ Electrical™ Specialized Power Systems трехфазовых синхронных и асинхронных машин.

Зная, что положение вращающегося кадра задаётся (где λ представляет собой скорость вращения кадра), преобразование αβ0 в dq0 выполняет вращение − (start.t) на пространственном векторе _Us = _uα + j· _uβ. Компонент гомополярной или нулевой последовательности остается неизменным.

В зависимости от выравнивания кадра при t = 0 компоненты dq0 выводятся из компонентов αβ0 следующим образом:

Когда вращающаяся рама выровнена по оси A, получаются следующие уравнения:

$\begin{array}{l} _{}_{}_{} Us=ud+j\cdotuq= (_{}_{} ua+j\cdotuβ)^{} \\ \begin{matrix} _{} \\ _{} \\ _{} \end{matrix} \begin{matrix} ⋅e−jωt[uduqu0]=[cos ( & startt) sin \\ (startt) 0 - & sin ( & startt \\ ) \end{matrix} cos \begin{matrix} _{(} \\ _{startt} \\ )_{} \end{matrix} \end{array}$ 0001] [uauβu0]

Обратное преобразование задается

$\begin{array}{l} _{uα} +_{j⋅uβ} =_{}_{} (ud+j\cdotuq)^{} \\ \begin{matrix} _{} \\ _{} \\ _{} \end{matrix} \cdotejωt[uαuβu0] \begin{matrix} = [\cos & (ωt) -sin \\ (ωt) & 0sin (ωt) \\ , потому что \end{matrix} \begin{matrix} _{} \\ (ωt) \\ _{} \end{matrix} \end{array}$ 0001] [uduqu0]

Когда вращающаяся рама выровнена на 90 градусов позади оси A, получаются следующие соотношения:

$\begin{array}{l} _{}_{}_{} Us=ud+j\cdotuq= (_{}_{} uα+j\cdotuβ)^{⋅e−j (\frac{}{startt}} \\ - \begin{matrix} _{} \\ {øb2}_{)} \\ _{[} \end{matrix} \frac{}{} \begin{matrix} uduqu0] = 23 & [\sin (\frac{startt}{)} & \sin (startt \frac{-}{} \\ 2ā3) sin & (startt + \frac{}{2ā3}) & cos (\frac{startt)}{} \\ \frac{}{cos} & \frac{}{(} & \frac{}{startt} \end{matrix} - \begin{matrix} _{} \\ _{2ā3} \\ )_{} \end{matrix} \end{array}$ cos (startt + 2ų 3) 121212] [uaubuc]

Обратное преобразование задается

$_{}_{} uα+j\cdotuβ= (_{}_{} ud+j\cdotuq)^{⋅ej (\frac{}{startt}}$ − ¼ 2)

Преобразование abc-в-альфа-бета-ноль, применяемое к набору сбалансированных трехфазных синусоидальных величин _ua, _ub, _uc, создает пространственный вектор _Us, координаты _uα и _uβ которого в фиксированном опорном кадре изменяются синусоидально со временем. В противоположность этому преобразование abc-dq0 (преобразование Парка), применяемое к набору сбалансированных трехфазных синусоидальных величин _ua, _ub, _uc, создает пространственный вектор _Us, координаты _ud и _uq которого в dq вращающейся системе отсчета остаются постоянными.

Параметры

Центровка поворотной рамы (при мас. =

Выбрать центровку поворотного каркаса, при wt = 0, компонентов dq0 трехфазного сбалансированного сигнала:

$_{ua} = \sin (startt_{);} ub = \frac{sin}{(} startt -_{} 2ā3); uc \frac{=}{}$ sin (

(величина положительной последовательности = 1,0 pu; фазовый угол = 0 градусов)

При выборе Aligned with phase A axis, компоненты dq0 - d = 0, q = − 1 и ноль = 0.

При выборе 90 degrees behind phase A axis, параметр по умолчанию, компоненты dq0 - d = 1, q = 0 и ноль = 0.

Входы и выходы

αβ0: Векторизированный αβ0 сигнал.
dq0: Векторизированный сигнал dq0.
wt: Угловое положение в радианах вращающейся рамы dq относительно неподвижной рамы.

Пример

power_Transformations Пример показывает различные применения блоков, выполняющих преобразования Кларка и Парка.

Представлен в R2013a

Документация