freqz использует алгоритм на основе БПФ для вычисления частотной характеристики Z-преобразования цифрового фильтра. В частности, заявление
[h,w] = freqz(b,a,p)
возвращает p-точечную комплексную частотную характеристику H (ejλ) цифрового фильтра.
(2) e − jλ +... + a (m + 1) e − jü m
В самом простом виде, freqz принимает векторы коэффициентов фильтра b и aи целое число p задание количества точек, в которых вычисляется частотный отклик. freqz возвращает комплексную частотную характеристику в векторе hи фактические частотные точки в векторе w в рад/с.
freqz может принимать другие параметры, такие как частота дискретизации или вектор произвольных частотных точек. Пример ниже находит 256-точечную частотную характеристику для фильтра типа I Чебышева 12-го порядка. Вызов freqz задает частоту выборки fs 1000 Гц:
[b,a] = cheby1(12,0.5,200/500); [h,f] = freqz(b,a,256,1000);
Поскольку список параметров включает частоту выборки, freqz возвращает вектор f который содержит 256 точки частоты между 0 и fs/2 используется при вычислении частотной характеристики.
Примечание
Эта панель инструментов использует правило, согласно которому единичной частотой является частота Найквиста, определяемая как половина частоты выборки. Параметр частоты отсечки для всех основных функций конструкции фильтра нормализуется частотой Найквиста. Для системы с частотой дискретизации 1000 Гц, например, 300 Гц составляет 300/500 = 0,6. Чтобы преобразовать нормированную частоту в угловую вокруг единичной окружности, умножьте на δ. Чтобы преобразовать нормализованную частоту обратно в герц, умножьте на половину частоты выборки.
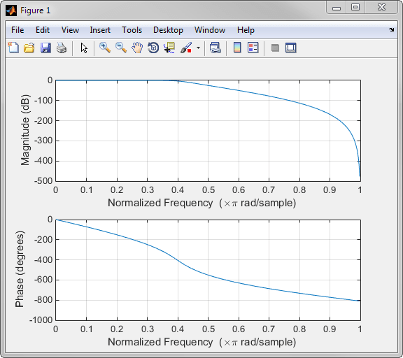
При звонке freqz без выходных аргументов строит график как величины в зависимости от частоты, так и фазы в зависимости от частоты. Например, фильтр нижних частот Баттерворта девятого порядка с частотой отсечки 400 Гц на основе частоты дискретизации 2000 Гц представляет собой
[b,a] = butter(9,400/1000);
Чтобы вычислить 256-точечную комплексную частотную характеристику для этого фильтра и построить график величины и фазы с помощью freqz, использовать
freqz(b,a,256,2000)
freqz может также принимать вектор произвольных частотных точек для использования в вычислении частотного отклика. Например,
w = linspace(0,pi); h = freqz(b,a,w);
вычисляет комплексную частотную характеристику в частотных точках в w для фильтра, определяемого векторами b и a. Частотные точки могут находиться в диапазоне от 0 до 2δ. Чтобы задать частотный вектор в диапазоне от нуля до частоты выборки, включите в список параметров и частотный вектор, и значение частоты выборки.
Эти примеры показывают, как вычислять и отображать цифровые частотные характеристики.
Вычислите и отобразите амплитудную характеристику фильтра нижних частот БИХ третьего порядка, описанную следующей передаточной функцией:
4461z-1 + 0 .7957z-2).
Выражайте числитель и знаменатель как многочленовые свертки. Найдите частотную характеристику в точках 2001, охватывающих всю единичную окружность.
b0 = 0.05634;
b1 = [1 1];
b2 = [1 -1.0166 1];
a1 = [1 -0.683];
a2 = [1 -1.4461 0.7957];
b = b0*conv(b1,b2);
a = conv(a1,a2);
[h,w] = freqz(b,a,'whole',2001);Постройте график амплитудной характеристики, выраженной в децибелах.
plot(w/pi,20*log10(abs(h))) ax = gca; ax.YLim = [-100 20]; ax.XTick = 0:.5:2; xlabel('Normalized Frequency (\times\pi rad/sample)') ylabel('Magnitude (dB)')

Сконструировать полосовой фильтр FIR с полосой пропускания от до рад/образец и 3 дБ пульсации. Первый стоп-диапазон находится в диапазоне от до рад/образец и имеет ослабление 40 дБ. Второй стоп-диапазон переходит от рад/образец к частоте Найквиста и имеет ослабление 30 дБ. Вычислите частотную характеристику. Постройте график его величины как в линейных единицах, так и в децибелах. Выделите полосу пропускания.
sf1 = 0.1; pf1 = 0.35; pf2 = 0.8; sf2 = 0.9; pb = linspace(pf1,pf2,1e3)*pi; bp = designfilt('bandpassfir', ... 'StopbandAttenuation1',40, 'StopbandFrequency1',sf1,... 'PassbandFrequency1',pf1,'PassbandRipple',3,'PassbandFrequency2',pf2, ... 'StopbandFrequency2',sf2,'StopbandAttenuation2',30); [h,w] = freqz(bp,1024); hpb = freqz(bp,pb); subplot(2,1,1) plot(w/pi,abs(h),pb/pi,abs(hpb),'.-') axis([0 1 -1 2]) legend('Response','Passband','Location','South') ylabel('Magnitude') subplot(2,1,2) plot(w/pi,db(h),pb/pi,db(hpb),'.-') axis([0 1 -60 10]) xlabel('Normalized Frequency (\times\pi rad/sample)') ylabel('Magnitude (dB)')

Сконструировать фильтр Баттерворта 3-го порядка, имеющий нормированную частоту 3-dB рад/образец. Вычислите его частотную характеристику. Выразите отклик величины в децибелах и постройте его график.
[b,a] = butter(3,0.5,'high'); [h,w] = freqz(b,a); dB = mag2db(abs(h)); plot(w/pi,dB) xlabel('\omega / \pi') ylabel('Magnitude (dB)') ylim([-82 5])

Повторить вычисление с помощью fvtool.
fvtool(b,a)

freqs оценивает частотную характеристику аналогового фильтра, определяемую двумя векторами входных коэффициентов, b и a. Его работа аналогична работе freqz; можно задать число используемых частотных точек, ввести вектор произвольных частотных точек и построить график величины и фазовой характеристики фильтра. В этом примере показано, как вычислять и отображать аналоговые частотные характеристики.
Спроектируйте аналоговый фильтр нижних частот Баттерворта 5-го порядка с частотой отсечки 2 ГГц. Умножьте на , чтобы преобразовать частоту в радианы в секунду. Вычислите частотную характеристику фильтра в 4096 точках.
n = 5;
f = 2e9;
[zb,pb,kb] = butter(n,2*pi*f,'s');
[bb,ab] = zp2tf(zb,pb,kb);
[hb,wb] = freqs(bb,ab,4096);Спроектируйте фильтр 5-го порядка Чебышева типа I с той же частотой кромки и 3 дБ пульсации полосы пропускания. Вычислите его частотную характеристику.
[z1,p1,k1] = cheby1(n,3,2*pi*f,'s');
[b1,a1] = zp2tf(z1,p1,k1);
[h1,w1] = freqs(b1,a1,4096);Проектирование фильтра 5-го порядка Чебышева типа II с той же частотой фронта и 30 дБ затухания полосы останова. Вычислите его частотную характеристику.
[z2,p2,k2] = cheby2(n,30,2*pi*f,'s');
[b2,a2] = zp2tf(z2,p2,k2);
[h2,w2] = freqs(b2,a2,4096);Сконструируйте эллиптический фильтр 5-го порядка с той же частотой краев, 3 дБ пульсации полосы пропускания и 30 дБ затухания полосы останова. Вычислите его частотную характеристику.
[ze,pe,ke] = ellip(n,3,30,2*pi*f,'s');
[be,ae] = zp2tf(ze,pe,ke);
[he,we] = freqs(be,ae,4096);Постройте график затухания в децибелах. Выражайте частоту в гигагерцах. Сравните фильтры.
plot(wb/(2e9*pi),mag2db(abs(hb))) hold on plot(w1/(2e9*pi),mag2db(abs(h1))) plot(w2/(2e9*pi),mag2db(abs(h2))) plot(we/(2e9*pi),mag2db(abs(he))) axis([0 4 -40 5]) grid xlabel('Frequency (GHz)') ylabel('Attenuation (dB)') legend('butter','cheby1','cheby2','ellip')

Фильтры Баттерворта и Чебышева типа II имеют плоские полосы пропускания и широкие переходные полосы. Фильтры Чебышева I типа и эллиптические фильтры быстрее скатываются, но имеют пульсацию полосы пропускания. Частотный вход функции проектирования типа II Чебышева задает начало полосы останова, а не конец полосы пропускания.