РЧ приемники усиливают сигналы и сдвигают их на более низкие частоты. Приемник сам вводит шум, который ухудшает качество принятого сигнала. Отношение сигнал/шум (SNR) на выходе приемника в конечном счете определяет пригодность приемника.
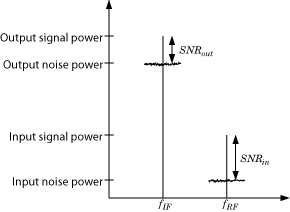
На предыдущем рисунке показано влияние приемника на сигнал. Приемник усиливает радиочастотный сигнал низкой мощности на несущей fRF с высоким SNR и преобразует сигнал с понижением частоты в fIF. Показатель шума (NF) системы определяет разность между SNR на выходе и SNR на входе:
NFsys
где разница рассчитывается в децибелах. Избыточное значение шума в системе приводит к тому, что шум подавляет сигнал, делая его нереализуемым.
Модель ex_simrf_snr моделирует упрощенную архитектуру приемника ПЧ. Синусоидальный блок и шумовой блок моделируют двухтональный вход, центрированный на уровне fRF и низкого уровня теплового шума. Радиочастотная система усиливает сигнал и смешивает его с гетеродином fLO до промежуточной частоты fIF. Датчик напряжения восстанавливает сигнал на ПЧ.
Для открытия этой модели в командной строке MATLAB ® введите:
addpath(fullfile(docroot,'toolbox','simrf','examples')) ex_simrf_snr
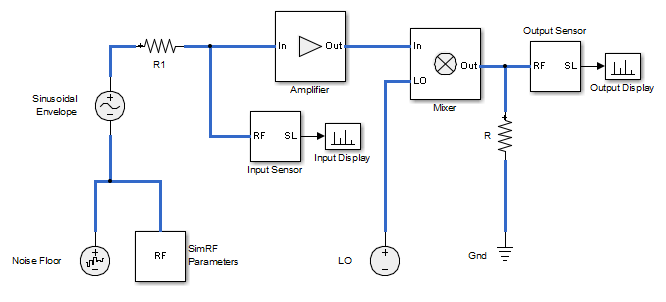
Усилитель вносит 40 дБ коэффициента усиления и показатель 15-dB шума, а смеситель - 0 дБ коэффициента усиления и показатель 20-dB шума, которые являются значениями, характерными для относительно шумного приемника с высоким коэффициентом усиления. Двухтональный вход имеет заданный уровень 0,1 мкВ. Уровень 1-V в гетеродине обеспечивает согласованность с составом коэффициента преобразования смесителя.
Для запуска модели:
Откройте модель, щелкнув ссылку или введя имя модели в командной строке.
Щелкните Выполнить (Run).
Для максимизации производительности параметры «Основные тона» и «Гармонический порядок» явно определяют частоты моделирования в блоке «Конфигурация»:
fLO, частота LO на первой стадии смешивания, равна 1,9999 ГГц. и появляется в списке фундаментальных тонов как carriers.LO.
fRF, несущая требуемого сигнала, равна 2 ГГц и появляется в списке фундаментальных тонов как carriers.RF.
fIF, промежуточная частота, равна fRF - fLO. Частота представляет собой линейную комбинацию (фундаментальных) гармоник fLO и fRF первого порядка. Установка гармонического порядка в 1 достаточна для обеспечения появления этой частоты в частотах моделирования. Это минимальное значение гармонического порядка обеспечивает минимум частот моделирования.
Условия решателя и настройки шума также задаются для блока Конфигурация (Configuration):
Для типа решателя установлено значение auto. Дополнительные сведения о выборе решателей см. на справочной странице блока «Конфигурация» или в разделе Выбор решателей Simulink ® и Simscape™ Solvers.
Параметр Sample time имеет значение 1/(mod_freq*64). Эта настройка обеспечивает пропускную способность моделирования в 64 раза большую, чем огибающие сигналы в системе.
Флажок Имитировать шум (Simulate noise) установлен, поэтому среда включает параметры шума во время моделирования.
Модель использует подсистемы с MATLAB Coder™ реализации быстрого преобразования Фурье (FFT) для генерации двух графиков. БПФ использует 64 ячейки, поэтому для частоты дискретизации 64 Гц полоса пропускания каждого ячейки равна 1 Гц. Затем уровни мощности, показанные на чертежах, также представляют спектральную плотность мощности (PSD) сигналов в дБм/Гц.
График входного дисплея показывает спектр мощности сигнала и шума на входе приемника.
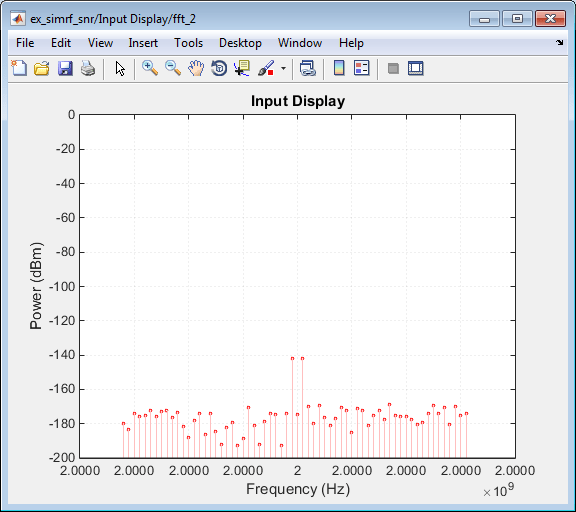
Измеренная мощность каждого тона согласуется с ожидаемым уровнем мощности 0.1-μV двухтональной огибающей:
30 = − 142 дБм
Коэффициент 1/2 обусловлен разделением напряжения на резисторах источника и нагрузки, а другой коэффициент 1/2 - масштабированием огибающей. Дополнительные сведения о масштабировании огибающих сигналов для расчета мощности см. в примере Двухтональный анализ огибающей с использованием реальных сигналов.
Измеренный уровень шума при -177 дБм/Гц уменьшается на 3 дБ от заданного уровня шума -174 дБм/Гц. Разница обусловлена передачей мощности от источника на вход усилителя. Усилитель также моделирует уровень теплового шума, поэтому, хотя это снижение нереально, оно не влияет на точность на выходном каскаде.
График выходного дисплея показывает спектр мощности сигнала и шума на выходе приемника.
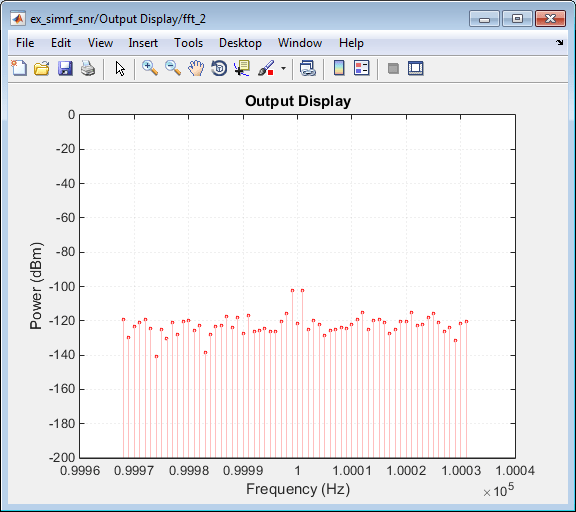
Измеренное значение PSD -102 дБм/Гц для каждого тонального сигнала соответствует 40-dB комбинированному коэффициенту усиления усилителя и смесителя. Шум PSD на рисунке показан на выходе примерно на 50 дБ выше из-за коэффициента усиления и шума системы.
Если установлено программное обеспечение DSP System Toolbox™, можно заменить подсистемы кодера MATLAB блоком Spectrum Analyzer (DSP System Toolbox).
Мощность теплового шума может быть смоделирована в соответствии с уравнением
4kBTRsΔf
где:
kB - постоянная Больцмана, равная 1,38065 × 10-23 Дж/К.
T - температура шума, заданная в данном примере как 293,15 К.
Rs - импеданс источника шума, заданный в данном примере как 50 Ом для согласования со значением сопротивления блока резистора с меткой R1.
Δf - ширина полосы шума.
Для моделирования уровня шума на РЧ сигнале на резисторе модель включает в себя шумовой блок:
Параметр спектральной плотности мощности шума (Вт/Гц) вычисляется как 4 кБТР.
Параметр Carrier frequences, значение carriers.RF, создает шум только на радиочастотной несущей.
Для моделирования радиочастотного шума на основе показателей шума компонентов:
Выберите «Имитация шума» в диалоговом окне «Параметры радиочастотного блока», если он еще не выбран.
Укажите значение параметра Noise figure (dB) блоков «Усилитель» и «Смеситель».
Шумовые показатели не являются строго аддитивными. Усилитель вносит больше шума в систему, чем смеситель, потому что он появляется первым в каскаде. Для вычисления суммарного шумового показателя ВЧ-системы с n ступенями используйте уравнение Фрииса:
− 1G1G2... Gn − 1
где Fi и Gi - коэффициент шума и коэффициент усиления i-го каскада, а NFi = 10log10 (Fi).
В этом примере показатель шума усилителя равен 10 дБ, а показатель шума смесителя равен 15 дБ, поэтому показатель шума системы равен:
10,0 дБ
Уравнение Фрииса показывает, что, хотя смеситель имеет более высокий показатель шума, усилитель вносит больше шума в систему.