Моделирование модели динамической системы позволяет получить представление о поведении предлагаемой конструкции системы без трудоемкого процесса фактического построения системы. Концепции в этом разделе предоставляют контекст для понимания того, как управлять моделированием модели с помощью программных средств Simulink ®.
Компиляция - это процесс Simulink, в котором блок-схема преобразуется во внутреннее представление, взаимодействующее с механизмом Simulink.
Нет наборов дифференциальных уравнений на уровне модели, которые решаются численно как единое целое. Вместо этого уравнения уровня модели соответствуют индивидуальным блочным уравнениям, которые решаются численно в определенном порядке.
Функциональность одного блока определяется несколькими уравнениями. Эти уравнения представлены в виде блочных методов. Эти блочные методы оцениваются (выполняются) во время выполнения блок-схемы. Оценка этих блочных методов выполняется в цикле моделирования, где каждый цикл через цикл моделирования представляет оценку блок-схемы в данный момент времени. Общие методы блоков включают в себя:
Производная - вычисляет производные непрерывных состояний блока на текущем временном шаге, учитывая входы блока и значения состояний на предыдущем временном шаге.
Обновить (Update) - вычисляет значение дискретных состояний блока на текущем шаге времени, учитывая его входные данные на текущем шаге времени и его дискретные состояния на предыдущем шаге времени.
Вывод (Output) - вычисляет выходы блока, заданные его входами на текущем шаге времени и его состояниями на предыдущем шаге времени.

В дополнение к методам блоков предоставляется набор методов, которые вычисляют свойства модели и ее выходные данные. Программное обеспечение Simulink аналогичным образом вызывает эти методы во время моделирования для определения свойств модели и ее выходных данных. Модельные методы обычно выполняют свои задачи, вызывая блочные методы одного типа. Например, метод выходных данных модели вызывает методы выходных данных блоков, которые он содержит, в порядке, заданном моделью для вычисления выходных данных. Метод модели «Производные» аналогично вызывает методы «Производные» блоков, которые он содержит, для определения производных его состояний.
См. также: Этапы моделирования в динамических системах.
Обратные вызовы - это выражения MATLAB, которые выполняются в ответ на определенное действие моделирования. Simulink предоставляет параметры обратного вызова модели, блока и порта, которые определяют определенные виды действий моделирования. Вы предоставляете код для параметров обратного вызова. Simulink выполняет код обратного вызова при выполнении связанного действия моделирования.
Параметры обратного вызова модели включают в себя:
PreloadFcn - выполняется перед загрузкой модели. Например, можно предоставить код, который загружает значения переменных, используемые моделью, в рабочую область MATLAB.
См. раздел Обратные вызовы модели.
Параметры блочного обратного вызова включают в себя:
OpenFcn - Выполнение при открытии блока подсистемы.
LoadFcn - Выполнить после загрузки схемы. Для блоков подсистемы также выполните параметры обратного вызова блока для блоков в блоке подсистемы.
Параметр обратного вызова порта:
ConnectionCallback - Выполнение кода при каждом изменении связности порта.
См. раздел Обратные вызовы портов.
Порядок выполнения - это последовательность, в которой методы блочного вывода вызываются после оценки прямого прохождения каждого входного порта. Чтобы отобразить порядок выполнения, на вкладке Отладка выберите Информационные наложения > Порядок выполнения.
В следующей модели сначала запускается выход блока интегратора, а затем цикл блоков, подключенных к входу блока интегратора. Пропущенные номера выполнения в последовательности обычно обусловлены скрытыми блоками буфера.
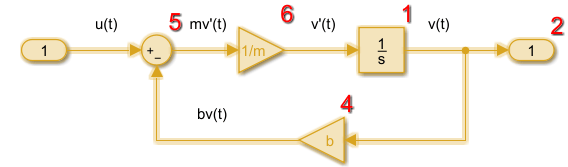
См. также: Управление и просмотр порядка выполнения, Фазы моделирования в динамических системах.
Моделирование - это процесс после компиляции модели, в котором выходные данные блочного метода и состояния вычисляются на последовательных временных шагах в заданном временном диапазоне с использованием числового решателя.
Во время каждого цикла моделирования Simulink вычисляет Δt для определения временного шага t(k+1) = t(k) + Δt. Размер Δt основан на оценочной ошибке между моделируемым решением и фактическим решением. В конце моделирования результаты данных приводятся в виде векторов. [t, X, Y] для времени, состояния и выходного сигнала на каждом временном шаге.
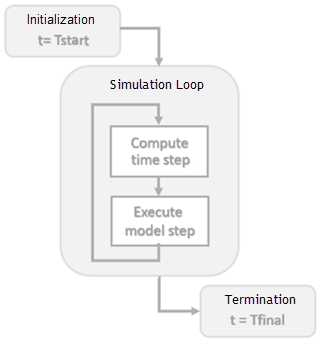
См. также: Фазы моделирования в динамических системах, Интерактивное моделирование модели, Ускорение моделирования.
Решатель находит приблизительное решение для набора уравнений модели. Simulink использует установленные числовые решатели для этой задачи.
Размер шага решателя может быть фиксированным или переменным:
Фиксированный шаг - Временной шаг T(k+1) = T(k) + Δt где Δt является постоянной. Если размер шага слишком велик, результаты моделирования могут иметь большую ошибку. В следующем примере размер шага равен 2 искажает форму синусоидального сигнала. Можно указать размер временного шага в случае решателей с фиксированным шагом, или решатель может автоматически определить размер шага в случае решателей с переменным шагом.
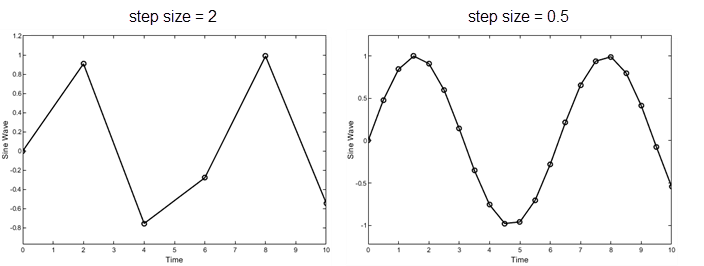
Шаг переменной - решатели шага переменной выполняют итерацию для достижения решения на основе допуска ошибки. Шаг времени T(k+1) = T(k) + Δtₖ где Δtₖ изменяется от одного этапа моделирования к следующему в зависимости от предполагаемой ошибки. Меньшие временные шаги повышают точность результатов моделирования. Чтобы минимизировать вычислительную нагрузку, решатель с переменным шагом выбирает наибольший размер шага, совместимый с достижением общего уровня точности, определяемого допуском ошибок и наблюдением пересечений нуля. Это гарантирует, что все состояния модели вычисляются с точностью, заданной пользователем.
Выбор метода решателя зависит от характера уравнений модели. Метод Эйлера является простым числовым решателем, который вычисляет следующее значение y с использованием уклона (y') касательной линии к y. Если y - функция, объединяющая наклонную функцию x с наклоном 1, y' = xи численный решатель будет использовать следующие уравнения.
x[n+1] = x[n] + Δt*1 y[n+1] = y[n] + Δt*x[n+1]
Уменьшение размера шага повышает точность результатов. но это увеличивает время на выполнение моделирования. В следующем примере размер шага равен 2 показывает ошибку около 20 процентов через 10 секунд, в то время как размер шага 0.5 дает результат, более близкий к фактическому решению.