Вы можете изучить stats структура, которая возвращается обеими nlmefit и nlmefitsaдля определения качества модели. stats структура содержит поля с условными взвешенными остатками (cwres поле) и отдельные взвешенные остатки (iwres поле). Поскольку модель предполагает, что остатки обычно распределены, можно изучить остатки, чтобы увидеть, насколько хорошо это предположение.
В этом примере синтетические данные генерируются с использованием обычных распределений. Он показывает, как выглядит статистика соответствия:
Хорошо при тестировании по тому же типу модели, что и при генерации данных
Плохо при тестировании на неверные модели данных
Инициализируйте модель 2-D со 100 отдельными пользователями:
nGroups = 100; % 100 Individuals nlmefun = @(PHI,t)(PHI(:,1)*5 + PHI(:,2)^2.*t); % Regression fcn REParamsSelect = [1 2]; % Both Parameters have random effect errorParam = .03; beta0 = [ 1.5 5]; % Parameter means psi = [ 0.35 0; ... % Covariance Matrix 0 0.51 ]; time =[0.25;0.5;0.75;1;1.25;2;3;4;5;6]; nParameters = 2; rng(0,'twister') % for reproducibility
Создайте данные для фитинга с пропорциональной моделью ошибок:
b_i = mvnrnd(zeros(1, numel(REParamsSelect)), psi, nGroups); individualParameters = zeros(nGroups,nParameters); individualParameters(:, REParamsSelect) = ... bsxfun(@plus,beta0(REParamsSelect), b_i); groups = repmat(1:nGroups,numel(time),1); groups = vertcat(groups(:)); y = zeros(numel(time)*nGroups,1); x = zeros(numel(time)*nGroups,1); for i = 1:nGroups idx = groups == i; f = nlmefun(individualParameters(i,:), time); % Make a proportional error model for y: y(idx) = f + errorParam*f.*randn(numel(f),1); x(idx) = time; end P = [ 1 0 ; 0 1 ];
Подгоните данные, используя ту же функцию регрессии и модель ошибок, что и генератор модели:
[~,~,stats] = nlmefit(x,y,groups, ... [],nlmefun,[1 1],'REParamsSelect',REParamsSelect,... 'ErrorModel','Proportional','CovPattern',P);
Создайте подпрограмму печати, скопировав следующее определение функции и создав файл plotResiduals.m на пути MATLAB ®:
function plotResiduals(stats) pwres = stats.pwres; iwres = stats.iwres; cwres = stats.cwres; figure subplot(2,3,1); normplot(pwres); title('PWRES') subplot(2,3,4); createhistplot(pwres); subplot(2,3,2); normplot(cwres); title('CWRES') subplot(2,3,5); createhistplot(cwres); subplot(2,3,3); normplot(iwres); title('IWRES') subplot(2,3,6); createhistplot(iwres); title('IWRES') function createhistplot(pwres) h = histogram(pwres); % x is the probability/height for each bin x = h.Values/sum(h.Values*h.BinWidth) % n is the center of each bin n = h.BinEdges + (0.5*h.BinWidth) n(end) = []; bar(n,x); ylim([0 max(x)*1.05]); hold on; x2 = -4:0.1:4; f2 = normpdf(x2,0,1); plot(x2,f2,'r'); end end
Постройте график остатков с помощью plotResiduals функция:
plotResiduals(stats);
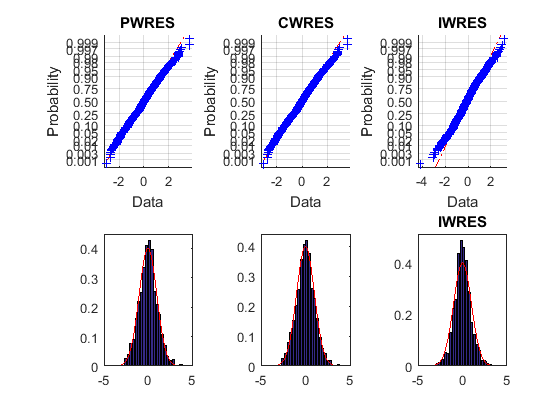
Графики верхней вероятности выглядят прямыми, что означает, что остатки обычно распределены. Графики нижней гистограммы соответствуют наложенному графику нормальной плотности. Таким образом, можно сделать вывод, что модель ошибки соответствует данным.
Для сравнения поместите данные с использованием постоянной модели ошибок вместо пропорциональной модели, которая создала данные:
[~,~,stats] = nlmefit(x,y,groups, ... [],nlmefun,[0 0],'REParamsSelect',REParamsSelect,... 'ErrorModel','Constant','CovPattern',P); plotResiduals(stats);
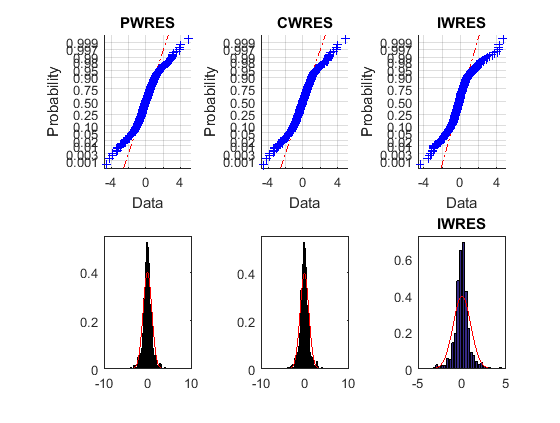
Верхние графики вероятности не являются прямыми, указывая на то, что остатки обычно не распределены. Графики нижней гистограммы довольно близки к наложенным графикам нормальной плотности.
Для другого сравнения поместите данные в модель структуры, отличную от модели, создавшей данные:
nlmefun2 = @(PHI,t)(PHI(:,1)*5 + PHI(:,2).*t.^4); [~,~,stats] = nlmefit(x,y,groups, ... [],nlmefun2,[0 0],'REParamsSelect',REParamsSelect,... 'ErrorModel','constant', 'CovPattern',P); plotResiduals(stats);
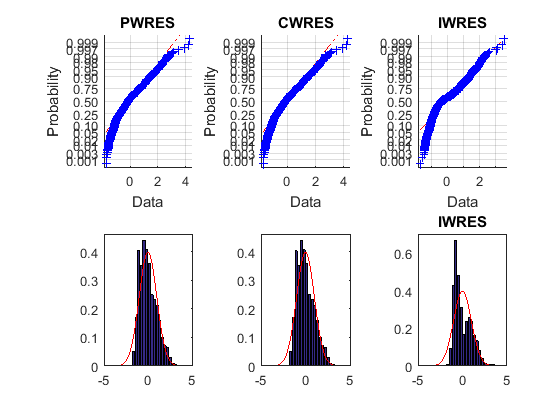
Графики верхней вероятности не являются прямыми. Кроме того, графики гистограммы довольно искажены по сравнению с наложенными графиками нормальной плотности. Эти остатки обычно не распределены и не соответствуют модели.